Стих про параллелограмм: Конкурс «Геометрические стихи»
Стихи о математике, математических понятиях.
Все эти стихотворения найдены мною в разное время на просторах всемирной паутины ( например, здесь), в старых детских книгах. Делюсь с вами найденным и предупреждаю: к моему сожалению, я не всегда могу указать настоящего автора произведений. Буду благодарна, если мы вместе с вами установим авторство.
А
Александр Городницкий
О, пластмасса угольников красных,И витое барокко лекала,
Геометрии стройная ясность,
Что со школы меня привлекала!
Медианы и хорды в тетради,
И изящные сны Пифагора!
Я родился и рос в Ленинграде,
Где учил геометрии город.
Предъявлял мне Васильевский остров
Параллели в ближайшей округе.
Пять углов вспоминаю я острых
И каналов гранитные дуги.
Возвращала мне каждая осень
Полукруглое арок свеченье
И лимонную улицу Росси,
Что квадрат образует в сеченье.
В этом мире, где всё по-другому,
Где и клином не вышибешь клина,
Я тоскую, как странник по дому,

Там ответы всегда беспристрастны,
Доказательства чёткие строги,
И прямые уходят в пространство,
Словно рельсы железной дороги.
Мы на вечность мимолётные мгновения,
Отрицая вероятность, что в финале
Эта функция закончится делением.
Путь к решению простой теперь и краткий,
В этой формуле не будет места скорби:
Сокращаются легко и без остатка
Наших чувств смешных неправильные дроби.
Завершилось вычисление совместное,
А итоги совершенно равноценные:
Ты уходишь в уравненье к неизвестному,
Я ищу себе другую переменную.
АРИФМЕТИКА
Чтоб водить корабли,
Чтоб в небо взлететь,
Надо многое знать,
Надо многое уметь.
И при этом, и при этом,
Вы заметьте-ка,
Очень важная наука
А-риф-ме-ти-ка!
Почему корабли
Не садятся на мель,
А по курсу идут
Сквозь туман и метель?
Потому что, потому что,
Вы заметьте-ка,
Капитанам помогает
А-риф-ме-ти-ка!
Чтоб врачом, моряком
Или летчиком стать,
Надо прежде всего
Арифметику знать.
И на свете нет профессии,
Вы заметьте-ка,
Где бы нам не пригодилась
А-риф-ме-ти-ка!
АРХИМЕД Д. Кедрин
Нет, не всегда смешон и узок
Мудрец, глухой к делам земли:
Уже на рейде в Сиракузах
Стояли римлян корабли.
Над математиком курчавым
Солдат занес короткий нож,
А он на отмели песчаной
Окружность вписывал в чертеж.
Ах, если б смерть — лихую гостью —
Мне так же встретить повезло,
Как Архимед, чертивший тростью
В минуту гибели — число!
Б
БАЛЛАДА О МАТЕМАТИКЕ
Как воздух, математика нужна,Самой отваги офицеру мало.
Расчеты! Залп! И цель поражена
Могучими ударами металла.
И воину припомнилось на миг,
Как школьником мечтал в часы ученья:
О подвиге, о шквалах огневых,
О яростном порыве наступленья.
 .
. Но строг учитель был,
И каждый раз он обрывал мальчишку грубовато:
— Мечтать довольно, повтори рассказ
О свойствах круга и углах квадрата.
И воином любовь сохранена
К учителю далекому, седому.
Как воздух, математика нужна
Сегодня офицеру молодому.
Баллада о математике
М. БорзаковскийКак воздух,
Математика нужна,
Одной отваги
Офицеру мало.
Расчеты! Залп!
И цель поражена
Могучими
Ударами
Металла.
И воину
Припомнилось на миг,
Как школьником
Мечтал в часы учения
О подвиге,
О шквалах огневых,
О яростном
Порыве наступления
Но строг учитель был,
И каждый раз
Он обрывал мальчишку
Резковато:
"Мечтать довольно!
Повтори рассказ
О свойствах круга
И углов квадрата!»
И воином
Любовь сбережена
К учителю,
Далекому, седому.
Как воздух.
Математика нужна,
Сегодня
Офицеру молодому!
БЕСКОНЕЧНОСТЬ
В мире, где все граница,
Все только предел и преграда,
Бездонная бесконечность —
Ты мне лишь одна награда.
В
Высота, медиана и биссектриса треугольника
Три девицы, три сестрицы
В треугольнике живут.
Речь такую там ведут:
— Всех главнее высота!
Говорю вам неспроста.
Видят все, как сторонам
Нужен перпендикуляр.
Тогда они, сменив названья,
Зовутся гордо — основанья!
— Нет, — сказала медиана, —
Спорить я не перестану.
И на это есть причина:
Я треугольника вершину
Соединяю с серединой
Стороны. К тому же я
Делю всю площадь пополам!
В спор вступила биссектриса:
— Спорить не имеет смысла!
Если трое соберемся,
В точке мы пересечемся.

Эта точка непростая.
Серединка золотая;
Если циркулем владеешь,
Окружность ты списать сумеешь!
Значит, всех я вас главнее!
В спор вмешался треугольник:
— Что вы, знает каждый школьник,
Что для меня вы все равны.
Будьте же всегда дружны!
Но вас предупреждаю я:
Знает каждый школьник,
Как меня построить.
К чему не проведут меня,
Всем перпендикулярна я.
Отгадай, вопрос простой,
Как зовусь я? (Высотой).
Вначале вы найти должны
Середину стороны.
Ее соединишь с вершиной,
И меня уж получил ты.
Просто все и без обмана.
Как зовусь я? (Медиана).
В.Высоцкий песни к спектаклю «Алиса в стране чудес»
Все должны до одного
Числа знать до цифры пять —
Ну, хотя бы для того,
Чтоб отметки различать.
Кто-то там домой пришел
И глаза поднять боится:
Это — раз, это — кол,
Это — единица.
За порог ступил едва,
А ему — головомойка:
Значит пара это два
Или просто двойка.

Эх, раз, еще раз,
Голова одна у нас,
Ну а в этой голове
Уха два и мысли две.
Вот и дразнится народ
И смеется глухо
Посмотрите — вот идет
Голова два уха
Голова, голова, голова два уха.
Г
ГАЛУА
Заходил паренек в сюртуке небогатом,
Чтобы в лавке табак и мадеру купить.
Приглашала любезно, как младшего брата,
Разбитная хозяйка и впредь заходить.
Провожала до двери, вздыхая устало,
Вслед ему разводила руками: «Чудак».
На 4 сантима опять обсчитала,
А 4 сантима теперь не пустяк!
Кто-то мне наболтал, будто видный ученый,
Математик какой-то мосье Галуа,
Как же может открыть мировые законы,
Эта вот, с позволенья сказать, голова?
Но всходил на мансарду обманутый ею,
Брал заветный набросок в чердачной пыли,
И доказывал вновь с беспощадностью всею,
Что хозяева сытых желудков — нули.
ГЕОМЕТРИЯ
О, Петр, ведь ты построил город
Не для умерших — для живых?
Тяжелый дождь бежит за ворот

Недвижимы аллеи парков,
Прямы проспекты, как стрела,
Сильней божественных монархов
Здесь геометрия была.
Был нежен в башнях цитадели
И кроток лепет голубиц,
И страшные на мир глядели
В окно глаза цареубийц!
Гуляют каменные финны,
Курятся трубки из бород,
Вот и построили Афины
Средь топей северных болот!
Налево львы и львы направо,
А у заставы инвалид
Штык держит вертикально прямо,
Как геометрия велит!
ГИМН ГИПОТЕНУЗЕ
Как символ вечного союза,
Как вечный символ знак простой,
Связала гипотенуза
Навеки катеты собой.
Путей окольных избегая
И древней истине верна,
Ты по характеру — прямая
И по обычаю — точна.
Скрывала тайну ты, но скоро
Явился некий мудрый грек
И теоремой Пифагора
Тебя прославил он навек.
Хранит тебя, безмолвно, чинно
Углов сторожевой наряд,
И копья — острые вершины
На обе стороны грозят.
И если двоечник, конфузясь,
Немеет пред твоим лицом.

Пронзит его, гипотенуза,
Своим отточенным копьем.
Гимн математике
Чтоб водить корабли ,
Чтобы в небо взлететь ,
Надо многое знать ,
И при этом , и при этом ,
Вы заметьте-ка ,
Очень важная наука
Ма-те-ма-ти-ка!
Почему корабли
Не садятся на мель ,
А по курсу идут
Сквозь туман и метель ?
Потому что, потому что,
Вы заметьте-ка ,
Капитанам помогает
Ма-те-ма-ти-ка!
Чтоб врачом, моряком
Или лётчиком стать.
Надо прежде всего
Математику знать.
И на свете нет профессий
Вы заметьте-ка,
Где бы вам не пригодилась
Математика!
Д
ДЕСЯТЬ ЧУДАКОВ
Их было десять чудаков,
Тех путников усталых,
Что в дверь решили постучать
Таверны «Славный малый».
— Пусти, хозяин, ночевать,
Не будешь ты в убытке.
Нам только ночку переспать,
Промокли мы до нитки.
Хозяин тем гостям был рад,
Да вот беда некстати:
Лишь девять комнат у него
И девять лишь кроватей.

Восьми гостям я предложу
Постели честь по чести.
Двоим придется ночь проспать
В одной кровати вместе.
Потом, вернувшись снова в «А»,
Где ждали его двое,
Он ключ от «И» вручить был рад
Тому герою.
Хоть много лет с тех пор прошло,
Неизвестно никому,
Как смог хозяин разместить
Гостей по одному.
Иль арифметика стара,
Иль чудо перед нами.
Понять, что, как и почему,
Вы постарайтесь сами.
Е
Ж
З
И
К
Квадратные единицы В большой толпе, Один из миллиона, 1м2=1000000мм2 Такой пригожий и удаленький 1мм2=0,000001м2 Квадратный миллиметр маленький. Мой нежный друг, Мой друг прелестный, Квадратный сантиметр чудесный! 1м2=10000см2 Из десяти тысяч ты один 1см2=0,0001м2 Такой нужный господин! Большой, широкий, ой-ой-ой, Квадратный дециметр мой.
 1м2=100дм2 Один из ста, моё спасенье, 1дм2=0,01м2 С таким я выдержу давление. Миллионную долю печали В напёрсток судьбы накачали – 1м3=1000000см3 И стал меланхолическим 1см3=0,000001м3 Сантиметр кубический.
1м2=100дм2 Один из ста, моё спасенье, 1дм2=0,01м2 С таким я выдержу давление. Миллионную долю печали В напёрсток судьбы накачали – 1м3=1000000см3 И стал меланхолическим 1см3=0,000001м3 Сантиметр кубический.Сказал я кругу: «Жизнь твоя – движенье. Ты ведь всегда в безудержном стремлении, Твой каждый шаг – начало и конец». Ответил круг: «Увы, моё движенье Не бег вперёд, а только возвращенье, Кусочек малый мне судьбою отведён, Навеки в нём как узник заключён».
Л
У дециметра смётка есть – Он ловко в куб сумел залезть, А так как трус был хитрым, 1дм3=1л. В быту назвался литром!
М
Математик
Это ложь, что в науке поэзии нет.
В отраженьях великого мира
Сотни красок со звуков уловит поэт
И повторит волшебная лира.
За чертогами формул, забыв о весне,
В мире чисел бродя, как лунатик,
Вдруг гармонию выводов дарит струне,
К звучной скрипке, прильнув, математик.
Настоящий учёный, он тоже поэт,
Вечно жаждущий знать и предвидеть.
Кто сказал, что в науке поэзии нет?
Нужно только понять и увидеть.
Н
О
Объём параллелепипеда «Бац!» – взмахнул кнутом пастух. «Пора вставать!» – пропел петух. Если слово «бац» запомнишь, Vпарал = bac Формулу объёма вспомнишь!
ОДИН
Почти дожив до глубоких седин,
Я понял арифметике назло,
Что у людей простейшее число «один»
Поистине сложнейшее число.
О логарифмах
Потому-то словно пена,
Опадают наши рифмы.
И величие степенно
Отступает в логарифмы.
Борис Слуцкий
Друзья, поверьте: самая интересная,
полезная и лирическая
Это – функция логарифмическая.
Спросите вы: «А чем интересна?»
А тем, что обратна она показательной
И относительно прямой y = x, как известно,
Симметричны их графики обязательно.
Проходит график через точку (1;0)
И в том еще у графика соль,
Что в правой полуплоскости он «стелется»,
А в левую попасть и не надеется.
Но, если аргументы поменяем,
Тогда по правилам кривую мы сдвигаем,
Растягиваем, если надо, иль сжимаем
И относительно осей отображаем.
Сама же функция порою убывает,
Порою по команде возрастает.
А командиром служит ей значенье α,
И подчиняется она ему всегда.
Многообразие применения показательной (или как ее еще называют экспоненциальной) функции вдохновили английского поэта Элмера Брила, он написал
«Оду экспоненте»:
«…Ею порождено многое из того,
Что достойно упоминания»,
Как говорили наши
Англосаксонские предки.
Могущество ее порождений
Заранее обусловлено ее
Собственной красотой и силой,
Ибо они суть физическое воплощение
Абстрактной идеи ее.
Английские моряки любят и знают ее
Под именем «Гунтер».
Две шкалы Гунтера –
Вот чудо изобретательности.
Экспонентой порождена
Логарифмическая линейка:
У инженера и астронома не было
Инструмента полезнее, чем она.
Даже изящные искусства питаются ею.
Разве музыкальная гамма не сеть
Набор передовых логарифмов?И таким образом абстрактно красивое
Стало предком одного из величайших
Человеческих достижений».
О НУЛЕ
Когда-то многие считали,
Что нуль не значит ничего.
И как ни странно, полагали,
Что нуль совсем не есть число.
Но на оси средь прочих чисел
Он все же место получил.
И все действительные числа
На два разряда разделил.
Коль нуль к числу ты прибавляешь,
Иль отнимаешь от него,
В ответе тотчас получаешь
Опять то самое число.
Попав, как множитель, средь чисел
Он сводит мигом все на нет.
И потому в произведеньи
Один за всех несет ответ.
А относительно деленья
Во-первых, нужно помнить то,
Что уж давно в научном мире
Делить на нуль запрещено.
Причина всем ведь очевидна,
А состоит причина в том,
Что смысла нет в таком деленьи
Противоречье в нем само.
О ТЕОРЕМЕ ПИФАГОРА
Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в далекий век.
Обильно было жертвоприношенье
Богам от Пифагора: сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет —
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
ОТ 1 ДО 10
(веселый счет)
Вот один иль единица
Очень тонкая, как спица.

А вот это цифра два,
Полюбуйся, какова!
Выгибает двойка шею,
Волочится хвост за нею.
А за двойкой — посмотри —
Выступает цифра три.
Тройка — третий из значков —
Состоит из двух крючков.
За тремя идут четыре,
Острый локоть оттопыря.
А потом пошла плясать
По бумаге цифра пять.
Руку вправо проятнула,
Ножку круто изогнула.
Цифра шесть — дверной замочек:
Верху крюк, внизу кружочек.
Вот семерка — кочерга,
У нее одна нога.
У восьмерки два кольца
Без начала и конца.
Цифра девять иль девятка —
Цифровая акробатка:
Если на голову встанет,
Цифрой шесть
девятка станет.
Цифра вроде -буквы «О» —
Это ноль иль ничего.
Круглый ноль такой хорошенький,
Но не знает ничегошеньки!
Если же слева рядом с ним
Единичку примостим,
Он побольше станет весить,
Потому что это — десять.
Эти цифры по порядку
Запиши в свою тетрадку.
От одного до десяти
... Не из учебника задача,
Вот один иль единица,
Очень тонкая как спица.
А вот это цифра два.
Полюбуйся, какова
Выгибает двойка шею,
Волочится хвост за нею.
А за двойкой - посмотри -
Выступает цифра три.
Тройка третий из значков. -
Состоит из 2х крючков.
За тремя идет четыре
Острый локоть оттопыря.
А потом пошла плясать
По бумаге цифра пять.
Руку влево протянула,
Ножку круто изогнула.
Цифра шесть - дверной замочек:
Сверху крюк, внизу кружочек.
Вот семерка - кочерга,
У нее одна нога.
У восьмерки два кольца
Без начала и конца.
Цифра девять иль девятка, -
Цифровая акробатка:
Если на голову встает,
Цифрой шесть девятка станет.
Цифра вроде буквы О
Это ноль, иль ничего:
Круглый ноль такой хорошенький,
Но не знает ничегошеньки!
Если ж слева, рядом с ним,
Единицу поместим,
Он побольше станет весить,
Потому что это - десять.
П
ПИФАГОРОВА ТЕОРЕМА
Не знаю, чем кончу поэму,
И как мне печаль избыть;
Древнейшую теорему
Никак я не в силах забыть.
Стоит треугольник, как ментор,
И угол прямой в нем есть.
И всем его элементам
Повсюду покой и честь.
Прелестная гипотенуза
Вознеслась так смело ввысь!
И с нею в вечном союзе
Два катета тоже взнеслись.
Она царит на квадратах
И песню поет она.
Та песня влечет куда-то
Геометров древних волна.
И все на торжищах света,
Как в огненном кольце,
И все повторяют это:
Ах, а, в, с!
И даже в холодной медузе
Огонь эта песня зажгла,
И все это гипотенузы
И катетов двух дела!
Плотность тела так найдём: Делим массу на объём.
 ρ = m : V
ρ = m : VПлощадь параллелограмма
Друзья мои, легко найти
S параллелограмма:
Вы помножьте а на b
И на синус гамма.
(S=absin)
Площадь трапеции
S трапеции ты знаешь.
Посчитай, я подожду.
Полусумму оснований
Ты умножь на высоту.
(S = (а+b/2)h)
Площадь треугольника
Площадь треугольника
Знать, конечно, надо:
Мы умножим а на аш
И разделим на два.
ПРОСТРАНСТВО
Пространству мера троякая:
В долготу бесконечно простирается,
В ширину беспредельно разливается,
В глубину она бездонно опускается!
Подражай сей мере в делах своих.
Р
На окружность градус будто Рассердился как-то круто. Говорит: «Я не слуга Мерить круглые бока, Поищи себе другого Измерителя такого!» И ушёл, забыв про дружбу, К треугольникам на службу.
 Видит радиус:
окружность Потеряла всю
наружность. Он дугой себя
согнул И к окружности
примкнул, А двум
радиусам – братцам С ним велел за
руки браться. Так был новый
угол дан Под названьем
радиан. Оказалось при
подсчётах, Шесть и
двадцать восемь сотых Этих радиусов
в ряд По окружности
лежат. В память
прочно закрепи: То число равно
2π. Нет прекрасней
радиана Для окружности
моей. Ну а градус,
как ни странно, Снова ищет
дружбы с ней.
В.С.Чикин
Видит радиус:
окружность Потеряла всю
наружность. Он дугой себя
согнул И к окружности
примкнул, А двум
радиусам – братцам С ним велел за
руки браться. Так был новый
угол дан Под названьем
радиан. Оказалось при
подсчётах, Шесть и
двадцать восемь сотых Этих радиусов
в ряд По окружности
лежат. В память
прочно закрепи: То число равно
2π. Нет прекрасней
радиана Для окружности
моей. Ну а градус,
как ни странно, Снова ищет
дружбы с ней.
В.С.Чикин С
Слово о математике
Почему торжественность вокруг?
Слышите, как быстро смолкла речь?
Это о царице всех наук
Начинаем мы сегодня вечер.
Не случайно ей такой почет.
Это ей дано давать ответы,
Как хороший выполнить расчет
Для постройки здания, ракеты.
Есть о математике молва,
Что она в порядок ум приводит,
Потому хорошие слова
Часто говорят о ней в народе.
Ты нам, математика, даёшь
Для победы трудностей закалку,
Учиться с тобой молодёжь
Развивать и волю и смекалку .
И за то, что в творческом труде
Выручаешь в трудные моменты,
Мы сегодня искренне тебе
Посылаем гром аплодисментов.
Чтобы в скорость жизнь вдохнуть, v = S : t Раздели на время путь. Сложение векторов
Как для слушателей лектор, Как приёмнику детектор, Так для силы нужен вектор. Как сложить две силы вместе? Отвечаем честь по чести: Стройте параллелограмм. Векторы по сторонам Начертить придётся нам. Для него диагонали Суммой векторною стали Силы, что мы с вами взяли, Ну а прочие детали Разберёшь в задачах сам. В.С.Чикин
Считалочка
Раз, два, три, четыре, пять,
Шесть, семь, восемь, девять, десять.
Можно все пересчитать,
Сосчитать, измерить, взвесить...
Сколько зерей в помидоре,
Сколько лодочек на море,
Сколько в комнате дверей,
В переулке фонарей,
Сколько камня на горе,
Сколько кошек во дворе.
Раз, два, три, четыре, пять,
Шесть, семь, восемь, девять, десять.
Можно все пересчитать,
Сосчитать, измерить, взвесить...
Сколько в комнате углов,
Сколько ног у воробьев,
Сколько пальцев на руках,
Сколько пальцев на ногах,
Сколько в садике скамеек,
Сколько в пяточке копеек.
Т
Теорема Виета. По праву достойна в стихах быть воспета О свойстве корней теорема Виета. Лишь корни умножишь и дробь уж готова В числителе «с», в знаменателе «а». Сумма корней тоже дроби равна, Хоть с минусом дробь эта – В числителе «в», в знаменателе «а».

ТОЧНОЕ ЧИСЛО
Поэтому мера свойственна обществу.
И все, что на небе, в душе, на земле,
Можно выразить в том числе.
Ты на меня, ты на него, на всех нас посмотри. У нас всего, у нас всего, у нас всего по три. Три стороны и три угла и столько же вершин. И трижды трудные дела мы трижды совершим. Все в нашем городе друзья, дружнее не сыскать. Мы треугольников семья, нас каждый должен знать. В. Житомирский, А. Шеврин «Геометрия для малышей». ТРЕУГОЛЬНИК И КВАДРАТ
Жили-были два брата:
Треугольник с квадратом
Старший — квадратный
Добродушный, приятный
Младший — треугольный,
Вечно недовольный.
Стал расспрашивать квадрат:
— Почему ты злишься, брат?
Тот кричит ему: — Смотри,
Ты полней меня и шире,
У меня углов лишь три,
У тебя же их четыре!
Но квадрат ответил: — Брат!
Я же старше, я — квадрат:
Я сказал еще нежней:
— Неизвестно, кто нужней!
Но настала ночь, и к брату,
Натыкаясь на столы,
Младший лезет воровато
Срезать старшему углы.
Уходя сказал:
— Приятных я тебе Желаю снов!
Знать, ложился — был квадратным,
А проснешься без углов!
Но наутро младший брат
Страшной мести был не рад.
Поглядел он — нет квадрата,
Онемел, стоял без слов…
Вот так месть! Теперь у брата
Восемь новеньких углов.
Тригонометрические функции
Шарада
Что кружится, что ложится
И на землю, и на крыши,
И о чем поэт зимою
По ночам поэмы пишет?
Это первое словечко.
А второе просто «на».
Ну, а третье? Угадайте,
Что бежит по проводам?
Напиши, что получилось,
И прочти наоборот.
Не запутайся, читая
Слово задом наперед!
(Снег-на-ток… котангенс).
С тригонометрией сейчас
Знакомы даже звери.
Правила все говорят
Четко и уверенно.
И попросим мы зверят
Рассказать их для ребят.
Как мы косинус считаем,
Ты спроси медузу.
— Делим прилежащий катет
На гипотенузу.
Синус вычислить сумеет
Зверь любой из лесной чащи:
На гипотенузу делит
Катет противолежащий.

Чтобы тангенс получить,
Нужно катеты делить.
Вы в числителе берете
Тот, что для угла напротив.
Тот, который прилежит,
В знаменателе пиши.
Если дробь перевернуть,
Это тоже верный путь!
Ты с конца прочти, дружок,
Как ложится «снег на ток».
— Как назвали отношенье катета к гипотенузе?
У кого ни спросим мы,
Отвечают: «Косинус».
Все мы думали-гадали:
Какой же они катет брали?
У
Учитель
(отрывок) С. Щипачев
... Не из учебника задача,
а потрудней открылся шифр.
Ребята поняли, что значит
простые с виду десять цифр.
Без них над ясностью речною
не возносились бы мечты;
на небо поглядев ночное,
о расстояние до звезды
нигде не вычитал бы ты...
Ф
Формула корней приведённого квадратного уравнения x2 + px + q = 0, x1 + x2 = — p и x1•x2 = q Чтобы решить уравненье, Корни его отыскать, Нужно немного терпенья, Ручка, перо и тетрадь.
 Минус «P» пополам Мы напишем вначале, Затем ± знак радикала, (С детства знакомого нам). А под корнем, приятель, Сводится всё к пустяку: «Р» пополам и в квадрате, Минус свободное q.
Минус «P» пополам Мы напишем вначале, Затем ± знак радикала, (С детства знакомого нам). А под корнем, приятель, Сводится всё к пустяку: «Р» пополам и в квадрате, Минус свободное q.
х1,2=
— р/2 ± √(р/2)2 – q , или D = р2 – 4q и х1,2 = ( -р ± √D):2
Х
Ц
Час, минута, секунда У часа 60 подруг По имени «минутки». Они стремительно бегут И заполняют сутки. В минуте 60 мгновений, 1ч = 60мин Зовут секундой их. 1мин = 60сек Они несут с собой волненья, Не проживёшь без них.
Числа
Мечтатели, сибиллы и пророки,
Дорогами, запретными для мысли,
Проникли — вне сознания — далёко,
Туда, где светят царственные числа.
Предчувствие разоблачает тайны,
Проводником нелицемерным светит:
Едва откроется намек случайный,
Объемлет нас непересказный трепет.
Вам поклоняюсь, вас желаю, числа!
Свободные, бесплотные, как тени,
Вы радугой связующей повисли
К раздумиям с вершины вдохновенья!
Числа
Я - обезумевший в лесу Предвечных Числ!Как взоры пристальны их роковых проблем!Предвечные, они - пред нами суть затем,Чтоб в вечности пребыть такими же!От их всевластных рук Вселенной не отымешь,Они лежат на дне и в сущности вещей,Нетленно проходя сквозь мириады дней.Я - обезумевший в лесу Предвечных Числ!Открою я глаза: их чудеса кругом!Закрою я глаза: они во сне самом!За кругом круг, в бессчетных сочетаньяхОни скользят в воспоминаньях.
Число «Пи»
Гордый Рим трубил победу
Над твердыней Сиракуз,
Но трудами Архимеда
Много больше я горжусь.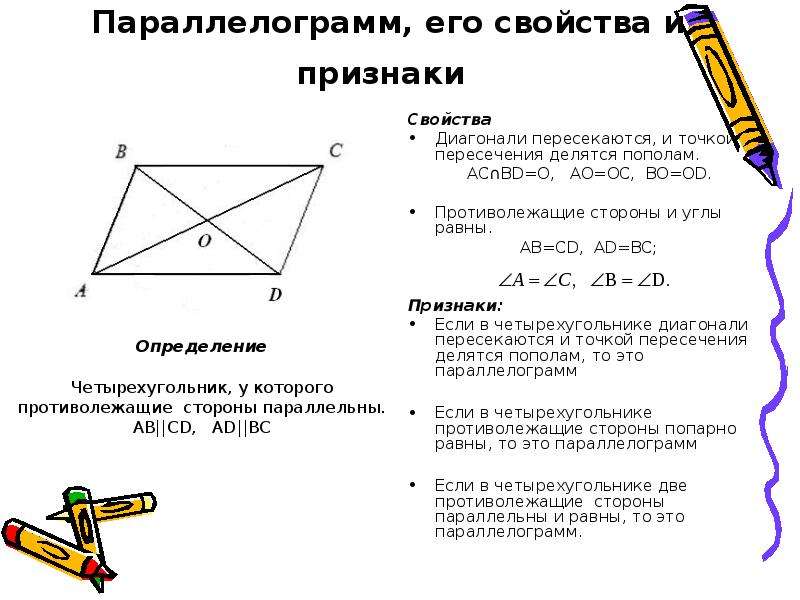
Надо нынче нам заняться,
Оказать старинке честь.
Чтобы нам не ошибаться,
Чтоб окружность верно счесть.
Надо только постараться
И запомнить все, как есть:
Три-14-15-92 и шесть.(п= 3,1415926)
Ш
Щ
ЭЭстрадное выступление
на математическом вечере
Наш юный друг!
Сегодня ты пришел вот в этот зал,
Чтоб помечтать, подумать, отдохнуть,
Увидеть наш концерт и «бал»,
Умом своим на все «взглянуть».
Сегодня вспомнишь формулу Герона,
Какую ты не раз писал
Ты вспомнишь также и Ньютона,
Бином которого познал.
Пусть в памяти твоей воскреснет Архимед,
Сраженный за великие творенья,
Пусть вспомнится известный всем Виет,
Открывший формулу для уравненья.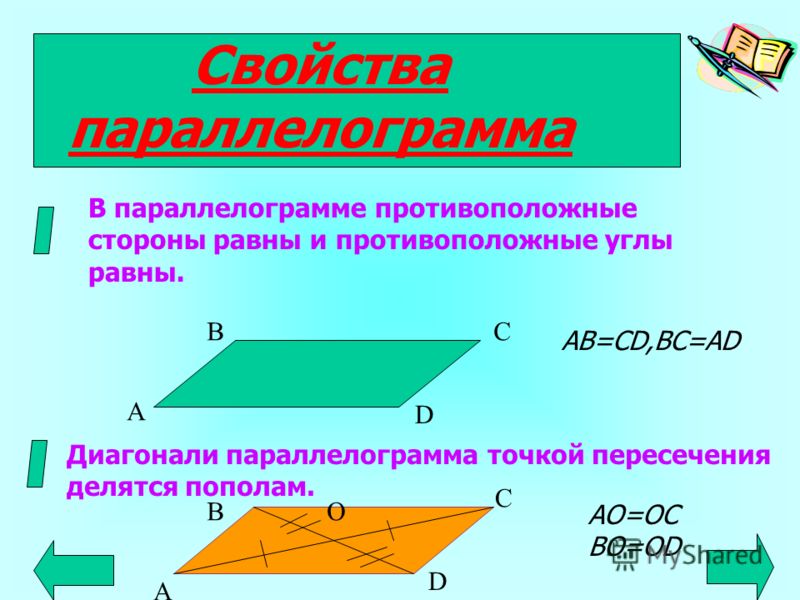
Тебе знаком талантливый Декарт —
Систем координат создатель.
Ты знаешь Лобачевского, он русский брат,
Коперник геометрии, творец, ваятель.
Велик и ныне Чебышев титан,
А Софья Ковалевская — чудесная «русалка»!
Талант могучий им был дан,
Дана была им гениальная смекалка.
Творцы великих мыслей и идей,
Какие род людской вынашивал столетья,
Пройдя сквозь бури трудных дней,
Переживут теперь тысячелетья.
Запомни то, что Гаусс всем сказал:
«Наука математика — царица всех наук»,
Не зря поэтому он завещал —
Творить в огне трудов и мук.
Безмерна роль ее в открытии законов,
В создании машин, воздушных кораблей,
Пожалуй, тpyдно нам пришлось бы без Ньютонов,
Каких дала история до наших дней.
Пусть ты не станешь Пифагором,
Каким хотел бы, может, быть!
Но будешь ты рабочим, может, и ученым,
И будешь честно Родине служить.
Ю
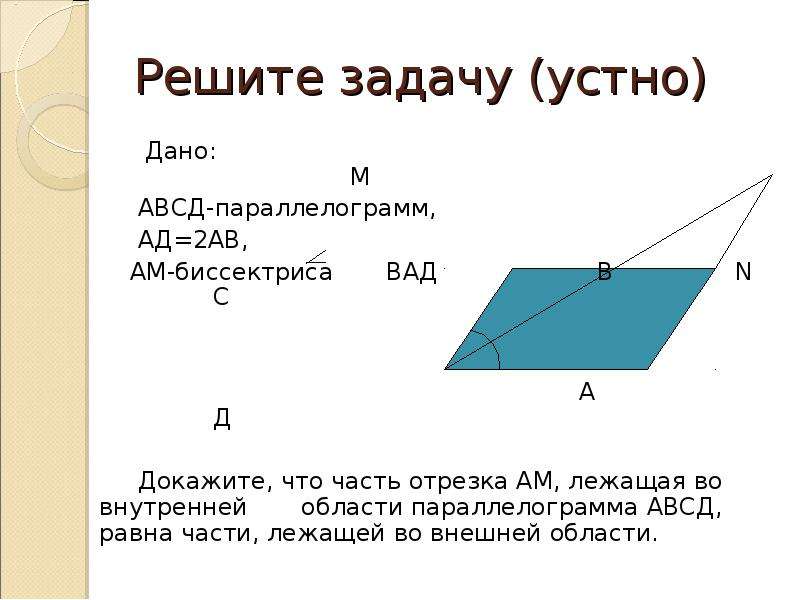
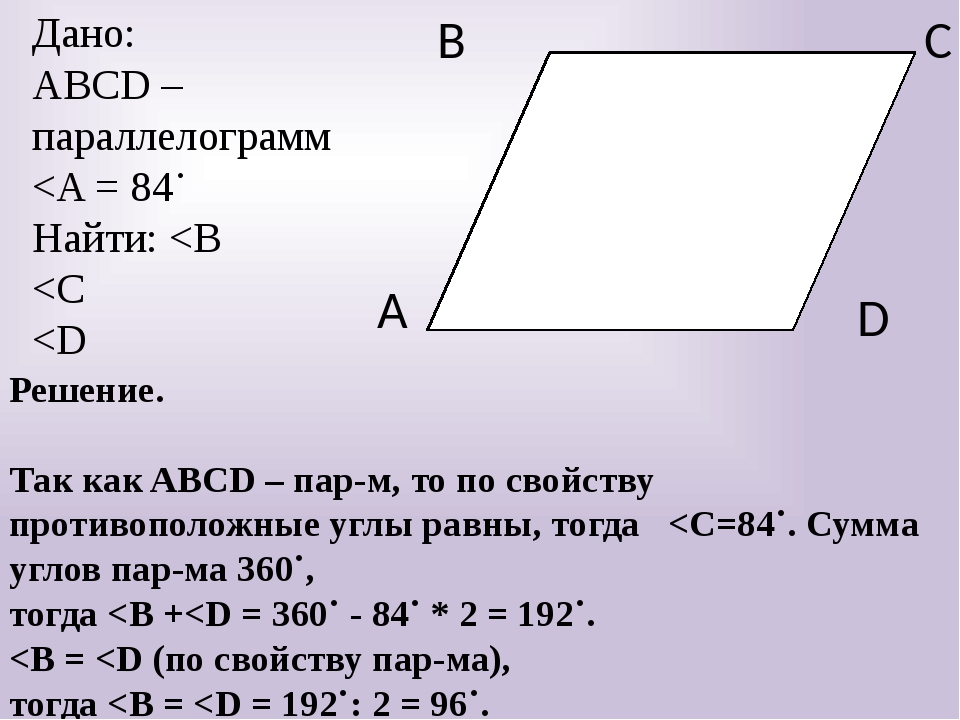
Решение задач по теме: «Параллелограмм» (1)
Три пути ведут к знанию:Путь размышления – это путь самый
благородный;
Путь подражания – это путь самый легкий;
Путь опыта – это путь самый горький.
Китайский философ и мудрец Конфуций.
Решение задач по
теме:
«Параллелограмм»
А2.
1. Один из углов
параллелограмма 138˚.
Найти остальные углы.
2. Сумма трех углов
параллелограмма равна
254˚. Найти углы
параллелограмма.
А2.
2. Периметр
параллелограмма 36 см, а
одна из его сторон больше
другой стороны в 2 раза.
Найти стороны
параллелограмма
А2.
3. Доказать, что АВСD параллелограмм.
В
2
С
4
3
A
1
D
Можно ли утверждать,
что четырехугольник, у
которого две стороны
параллельны,
а
две
другие
равны,
есть
параллелограмм?
• Нет
Назовите наименьшее
число элементов
параллелограмма,
которыми он однозначно
определяется.

• 2 смежные стороны и угол
между ними
• 2 смежные стороны и
диагональ
На какой угол нужно
повернуть
параллелограмм вокруг
точки пересечения
диагоналей, чтобы он
совместился сам с
собой?
11. Есть ли высота у параллелограмма?
• Сколько высот в параллелограмме?Может ли диагональ
параллелограмма быть
равной одной из его
высот?
13. Может
14. Б2. ABCD – параллелограмм. Найти углы
40˚Б2.
2. Полупериметр
параллелограмма 26 см,
а сумма двух сторон – 22
см. Найти стороны
параллелограмма.
Б2.3. АСМN – параллмм. ОМ=МВ, ОN=ND
Док-ть: АВСD – параллмм В
М
С
О
N
A
D
17. Сколько треугольников и сколько пар равных треугольников?
Почему сумма расстоянийлюбой точки, лежащей
внутри параллелограмма,
до всех его сторон есть
величина постоянная?
Один из углов параллелограмма
составляет 25% другого его угла.

Найти углы параллелограмма.
144˚ и 36˚
Стороны параллелограмма
равны a и b (b
отрезки, на которые
биссектриса угла
параллелограмма делит
его большую сторону.
a
В
С
b
А
D
23. Синквейн
• Синквейн (от фр. cinquains, англ.cinquain) – это творческая работа,
которая имеет короткую форму
стихотворения, состоящего из пяти
нерифмованных строк.
• Синквейн – это не простое
стихотворение, а стихотворение,
написанное по следующим правилам:
24. Cинквейн — пятистрочный белый стих
• 1. Одно существительное – тема синквейна.• 2. Два прилагательных или причастия,
раскрывающие тему.
• 3. Три глагола, описывающие действия,
относящиеся к теме, характеризующие или
объясняющие суть происходящих событий.
• 4. Фраза (предложение) из четырех слов,
позволяющая ученику выразить свое отношение к
теме или содержащая вывод (может
использоваться цитата, крылатое выражение).
• 5. Одно слово – резюме, дающее новую
интерпретацию темы; содержащее ассоциацию с
ней; восклицание. Завершение темы, синоним
первого слова, выраженный любой частью речи.
25. Cинквейн
• 1 существительное• 2 прилагательных
или причастия
• 3 глагола
• Фраза
• Резюме 1 слово
4 слова
Смежные углы.
Красивы, но не всегда равны.
Чертим, измеряем и знаем,
Что сумма их равна 180˚.
Теорема.
27. Диагональ
Презентация по теме «четырехугольники» — математика, презентации
Подготовил
Ученик 8 класса
Ромасюков Валера
План проекта.
1. Всё вокруг – геометрия
2. Определение четырёхугольника
3. Стихотворение
4. Генеалогическое древо
5. Виды четырёхугольников
6.Определение параллелограмма
7. Определение ромба
8. Определение прямоугольника
9. Определение квадрата
Определение квадрата
10.Стихотворение
11. Определение трапеции
Всё вокруг — геометрия.
«Я думаю, что никогда, до настоящего времени, мы не жили в такой геометрический период. Всё вокруг – геометрия». Эти слова великого французского архитектора Ле Корбюзье очень точно характеризуют и наше время. Мир, в котором мы живём, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Лучше ориентироваться в нём, открывать новое, понимать красоту и мудрость окружающего мира поможет вам эта наука.
Геометрия зародилась в глубокой древности. Строя жилища и храмы, украшая их орнам6нтами, размечая территории на поверхности земли, измеряя расстояния и площади зем6льных участков, человек применял свои знания о форме, размерах и взаимном расположении предметов, использовал свои геометричски5 знания, полученные из наблюдений и опытов. Почти все учёные древности и средних веков были выдающимися геометрами.
Геометрия изучает форму и взаимное расположение фигур.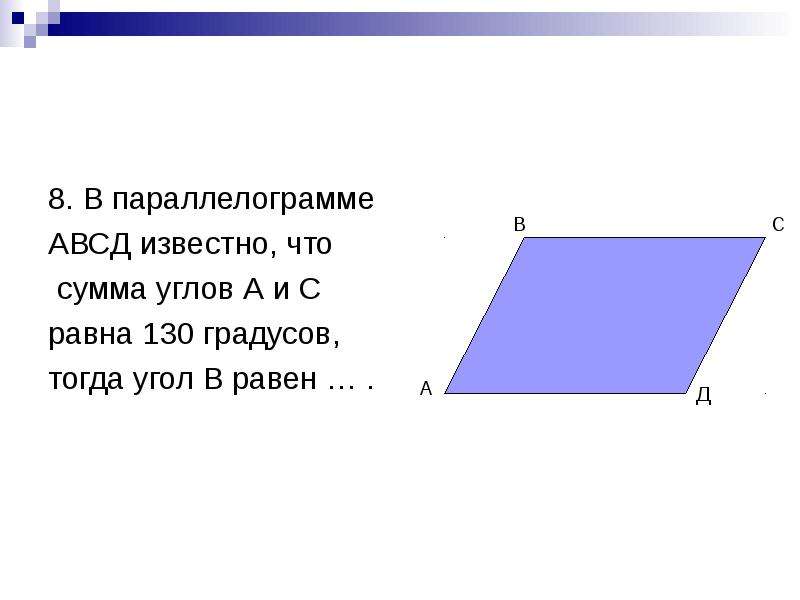
Четырёхугольники
Четырехугольником называется фигура, которая состоит из четырёх сторон и четырёх последовательно соединяющих их отрезков.
Вершины четырёхугольника называются соседними, если они являются концами одной из его сторон.
Вершины, не являющихся соседними, называют противолежащими.
Стороны четырёхугольника, исходящие из одной вершины, называются соседними сторонами.
Отрезки, соединяющие противоположные вершины четырехугольника называют диагоналями.
Стихотворение
Четырёхугольник фигурист,
Состоит из точек и вершин,
А его отрезки противолежащие
Стороны же исходящие!!!
Генеалогическое древо четырёхугольников
Виды четырёхугольников
Выпуклый
Четырёхугольник
Параллелограмм
Трапеция
Равнобедренная Квадрат Прямоугольник Ромб
Прямоугольная
Параллелограмм
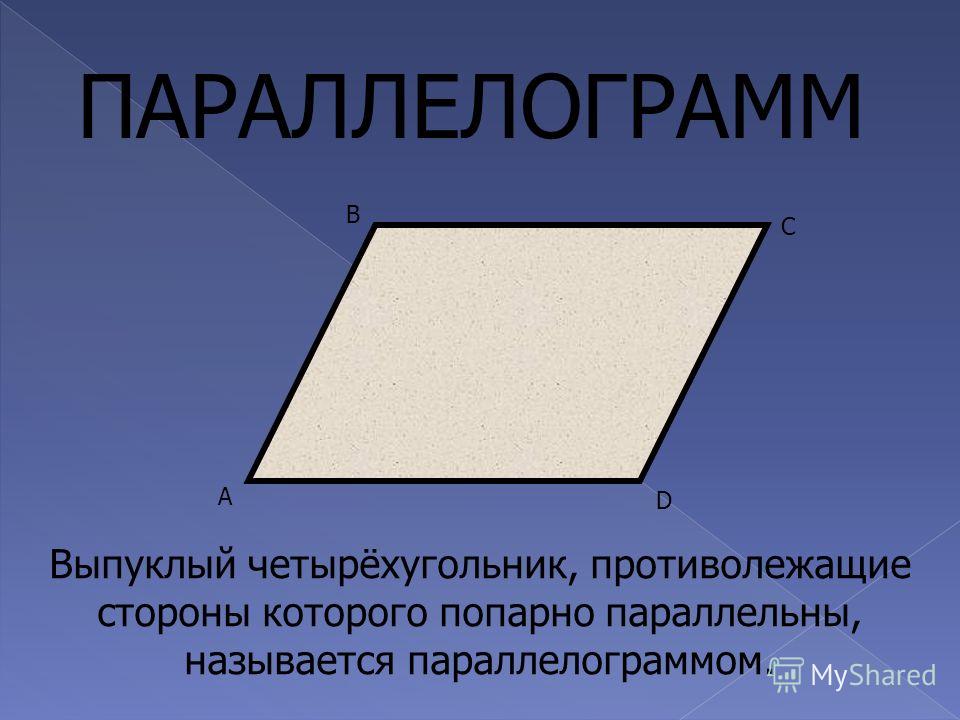
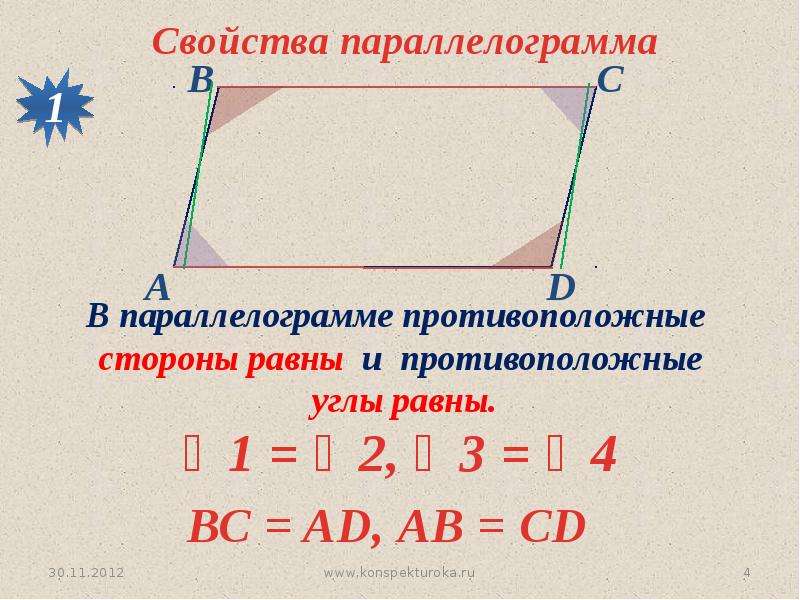
Четырёх угольник у которого противоположные стороны попарно параллельны, называются параллелограммом.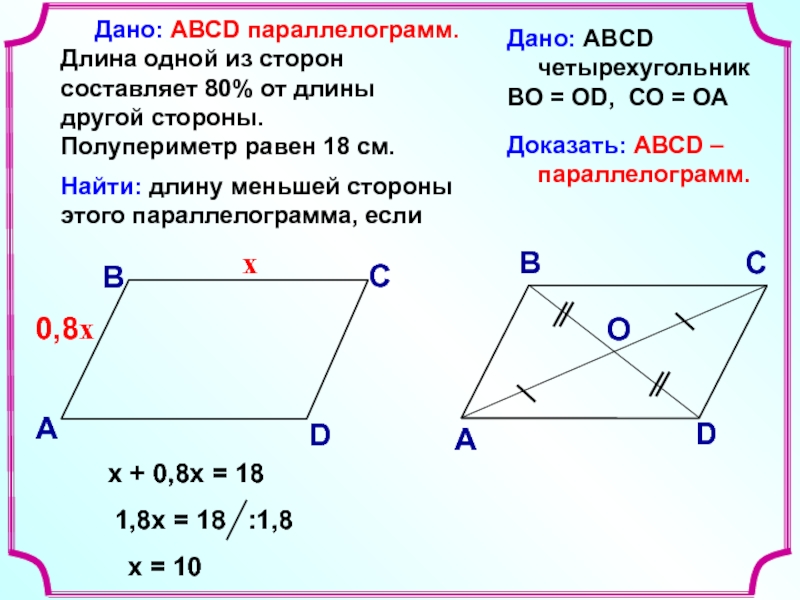
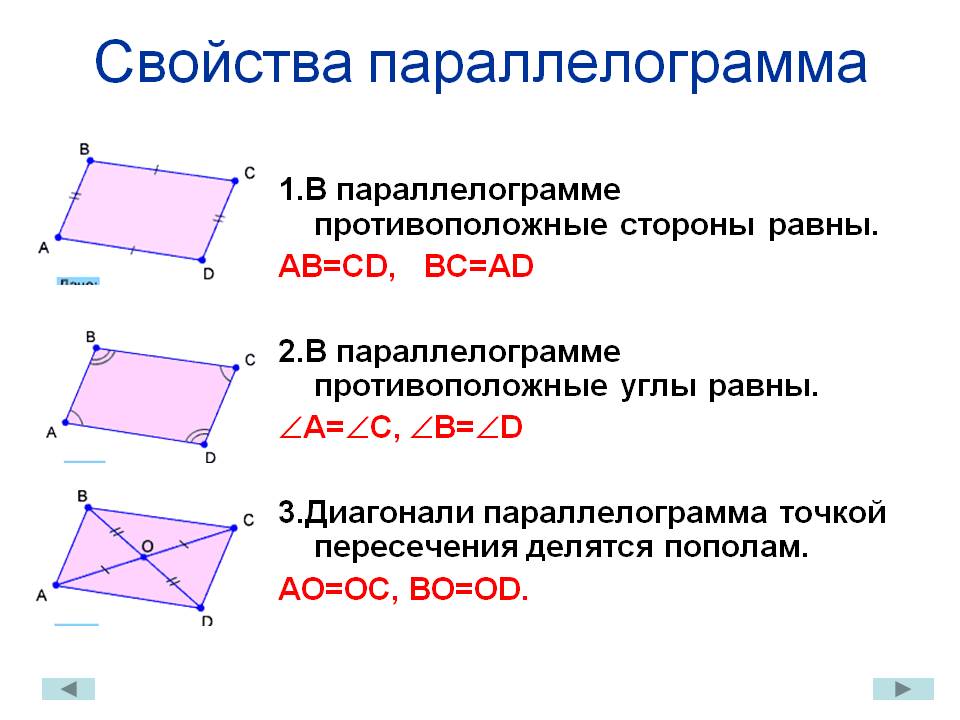
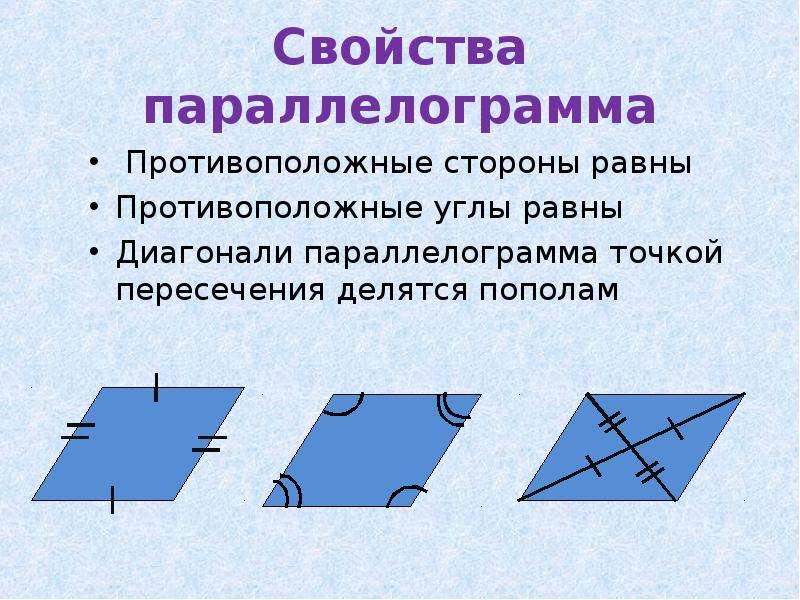
Свойства параллелограмма:
- Противоположные стороны равны;
- Противоположные углы параллелограмма равны;
- Каждая диагональ параллелограмма делит его на два равных треугольника;
- Диагонали параллелограмма делятся точкой пересечения пополам.
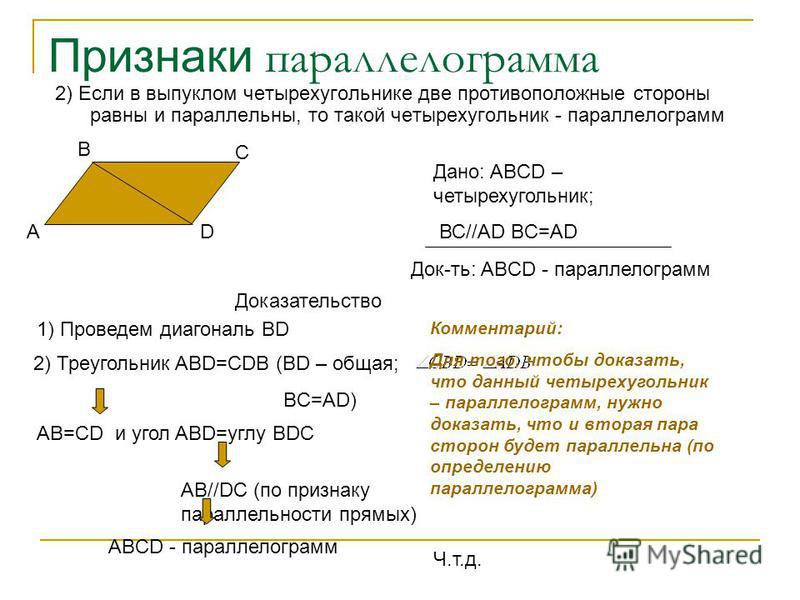
Признаки параллелограмма:
- Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёх угольник-параллелограмм.
- Если в четырёхугольнике две противоположные стороны равны и параллельны, то этот четырёхугольник-параллелограмм.
Каждый из признаков параллелограмма может быть взят в качестве определения параллелограмма.
Так из первого признака получаем определения следующее параллелограмма.
Четырёх угольник, у которого противоположные стороны попарно равны, называется параллелограммом.
Сумма внутренних углов параллелограмма
равна 360 ° .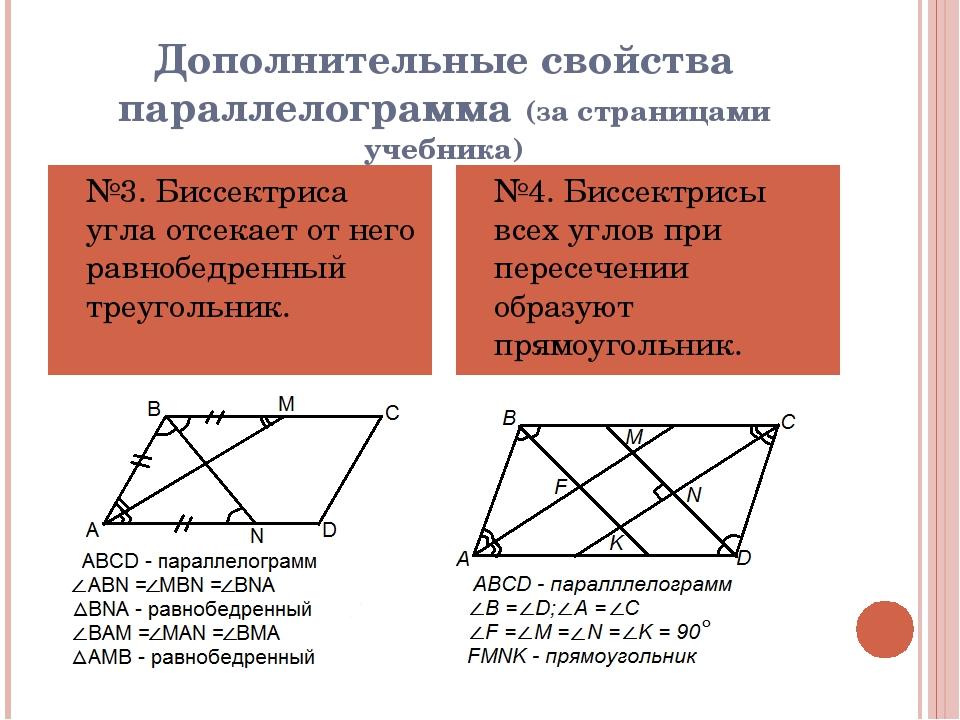
Отрезок перпендикуляра к сторонам параллелограмма, заключённый между ними, называется высотой параллелограмма.
Площадь параллелограмма равна произведению его основания на высоту:
S=ah
B
C
h
A
D
Ромб
Параллелограмм все стороны которого равны, называется площадь. Помимо всех свойств параллелограмма, ромб обладает следующими специальными свойствами:
- Диагонали ромба взаимно перпендикулярны;
- Диагонали ромба являются биссектрисами его внутренних углов.
- Диагонали ромба делят его внутринии углы пополам.
Площадь ромба может быть вычислена по формуле:
S=1/2d 1 d 2
Где d1 и d2 –диагонали ромба.
d2
d1
Прямоугольник
Параллелограмм все углы, у которого прямые называется прямоугольник.
Помимо всех свойств параллелограмма, прямоугольник обладает следующими специальными свойствами:
- Диагонали прямоугольника равны.
Признаки прямоугольника:
- Если в параллелограмме диагонали равны, то этот параллелограмм-прямоугольник.
Площадь прямоугольника вычисляется по формуле :
S=ab
Где a и b — смежные стороны.
b
a
a
b
Квадрат
Прямоугольник у которого все стороны равны называется квадратом.
Из определения квадрата и ромба следует, что квадрат это ромб у которого все углы прямые. Так как квадрат является и параллелограммом, и прямоугольником, и ромбом, то все свойства этих фигур присущи и квадрату.
Площадь квадрата вычисляется по формуле:
S=a²
a
a
a
a
Стихотворение
Квадрат поехал в Ленинград
И там узнали про квадрат
Что все сторонки равные
Углы прямые, славные.
Трапеция
Четырехугольник, две стороны которого параллельны, а две другие не параллельны, называется трапецией.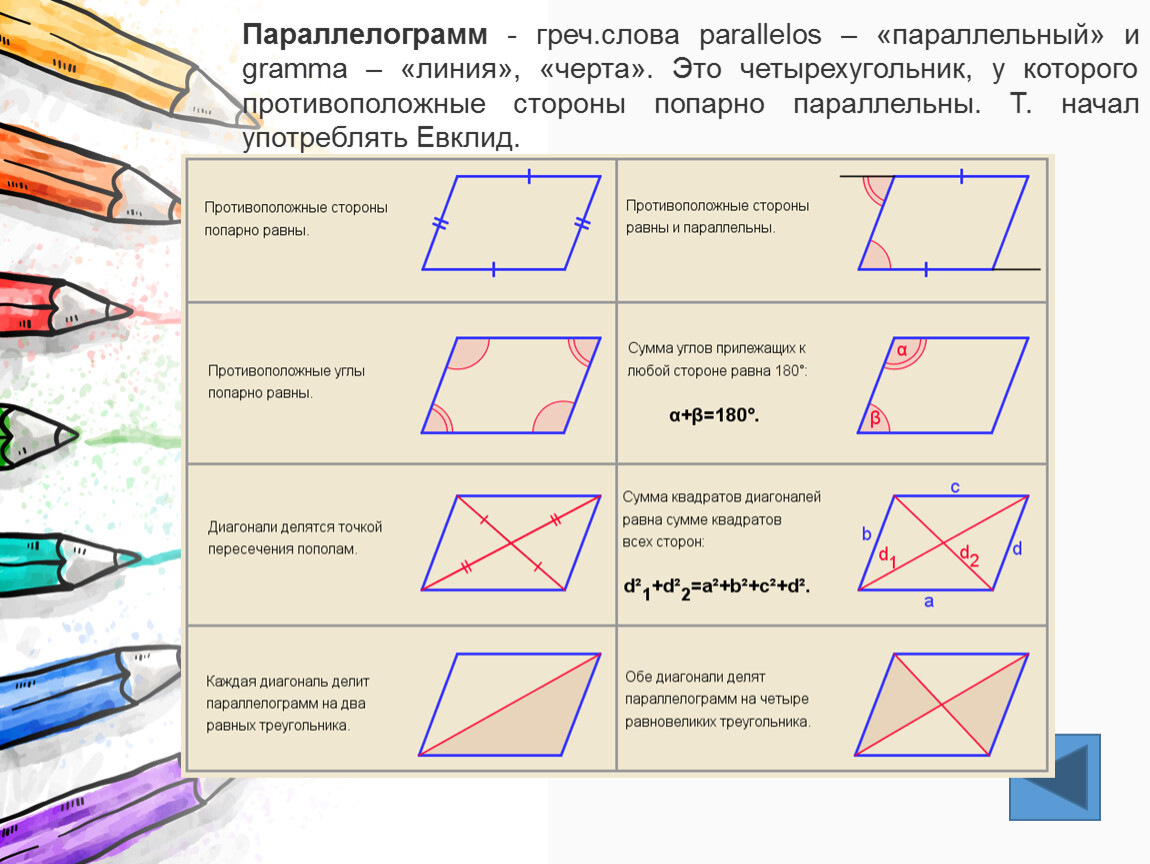
Паралельные стороны трапеции называют её основаниями, а не паралельные боковыми сторонами (ВС и АД-основания, АВ и СД-боковые стороны)
Отрезок перпендикуляра к основаниям трапеции, заключённый между основаниями называется высотой трапеции (ВН- высота). Трапеция, боковые стороны которой равны называется равнобедренной (или равнобочной).
В
С
Н
А
Д
В равнобедренной трапеции углы при основании равны:
Угол ВАД=АДС , а угол АВС=ВСД
Площадь трапеции вычисляется по формуле :
S=1/2(a+b)*h
a
h
b
Все правила про параллелограмм. Параллелограмм и его свойства
1. Определение параллелограмма.
Если пару параллельных прямых пересечём другой парой параллельных прямых, то получим четырёхугольник, у которого противоположные стороны попарно параллельны.
В четырёхугольниках ABDС и ЕFNМ (рис.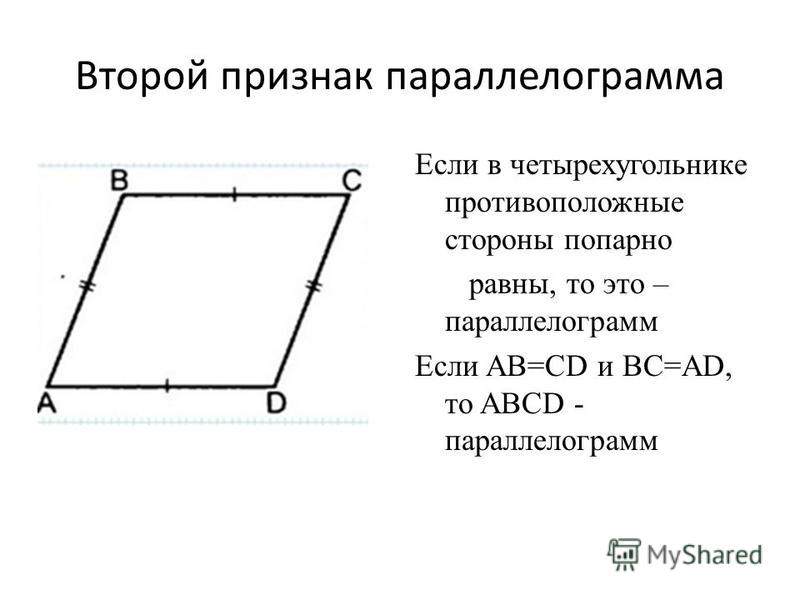 224) ВD || АС и AB || СD;
224) ВD || АС и AB || СD;
ЕF || МN и ЕМ || FN.
Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
2. Свойства параллелограмма.
Теорема . Диагональ параллелограмма делит его на два равных треугольника.
Пусть имеется параллелограмм ABDС (рис. 225), в котором AB || СD и АС || ВD.
Требуется доказать, что диагональ делит его на два равных треугольника.
Проведём в параллелограмме ABDС диагональ СВ. Докажем, что \(\Delta\)CAB = \(\Delta\)СDВ.
Сторона СВ общая для этих треугольников; ∠ABC = ∠BCD, как внутренние накрест лежащие углы при параллельных AB и СD и секущей СВ; ∠ACB = ∠СВD, тоже как внутренние накрест лежащие углы при параллельных АС и ВD и секущей CB.
Отсюда \(\Delta\)CAB = \(\Delta\)СDВ.
Таким же путём можно доказать, что диагональ AD разделит параллелограмм на два равных треугольника АСD и ABD.
Следствия:
1 .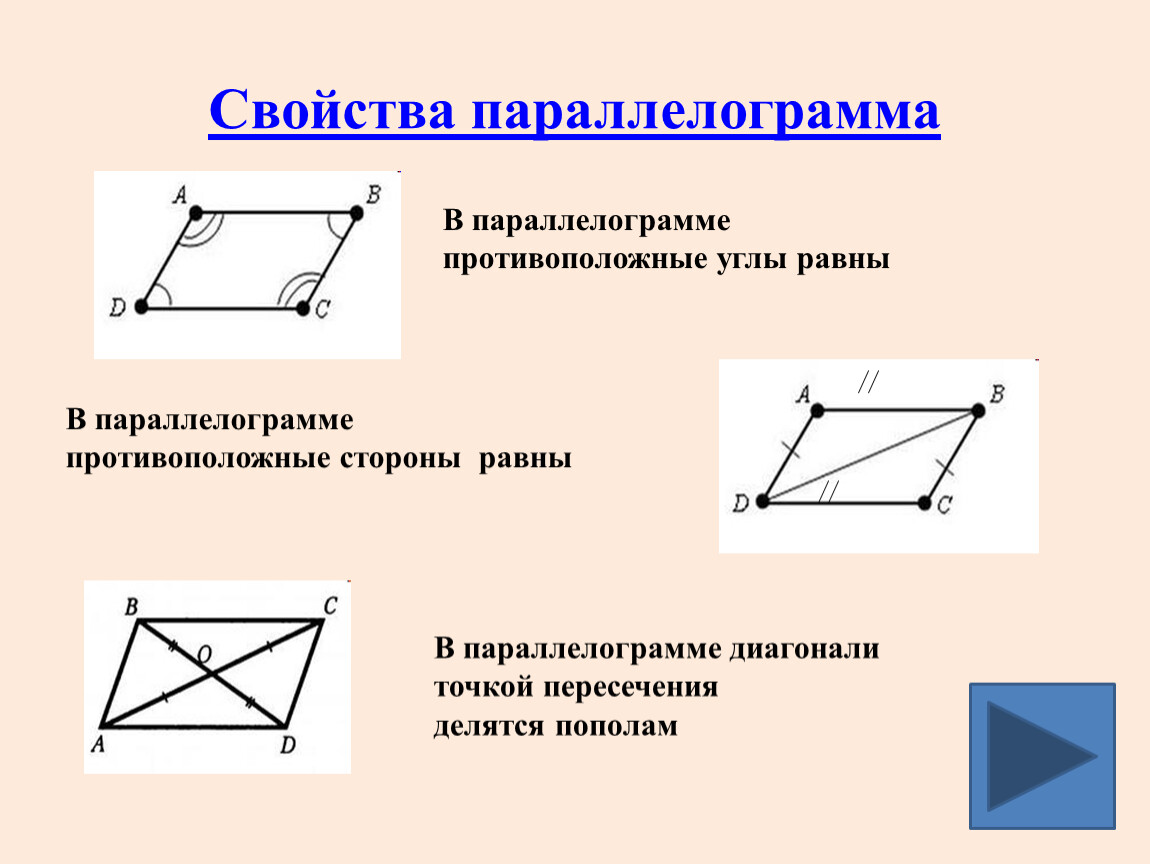 Противоположные углы параллелограмма равны между собой.
Противоположные углы параллелограмма равны между собой.
∠А = ∠D, это следует из равенства треугольников CAB и СDВ.
Аналогично и ∠С = ∠В.
2. Противоположные стороны параллелограмма равны между собой.
AB = СD и АС = ВD, так как это стороны равных треугольников и лежат против равных углов.
Теорема 2. Диагонали параллелограмма в точке их пересечения делятся пополам.
Пусть BC и AD — диагонали параллелограмма AВDС (рис. 226). Докажем, что АО = OD и СО = OB.
Для этого сравним какую-нибудь пару противоположно расположенных треугольников, например \(\Delta\)AOB и \(\Delta\)СОD.
В этих треугольниках AB = СD, как противоположные стороны параллелограмма;
∠1 = ∠2, как углы внутренние накрест лежащие при параллельных AB и СD и секущей AD;
∠3 = ∠4 по той же причине, так как AB || СD и СВ — их секущая.
Отсюда следует, что \(\Delta\)AOB = \(\Delta\)СОD. А в равных треугольниках против равных углов лежат равные стороны. Следовательно, АО = OD и СО = OB.
Следовательно, АО = OD и СО = OB.
Теорема 3. Сумма углов, прилежащих к одной стороне параллелограмма, равна 180° .
В параллелограмме ABCD проведем диагональ АС и получим два треугольника ABC и ADC.
Треугольники равны, так как ∠1 = ∠4, ∠2 = ∠3 (накрест лежащие углы при параллельных прямых), а сторона АС общая.
Из равенства \(\Delta\)ABC = \(\Delta\)ADC следует, что AB = CD, BC = AD, ∠B = ∠D.
Сумма углов, прилежащих к одной стороне, например углов А и D, равна 180° как односторонних при параллельных прямых.
Это четырёхугольник, противоположные стороны которого попарно параллельны.
Свойство 1 . Любая диагональ параллелограмма делит его на два равных треугольника.
Доказательство . По II признаку (накрест лежащие углы и общая сторона).
Теорема доказана .
Свойство 2 . В параллелограмме противолежащие стороны равны, противолежащие углы равны.
Доказательство
.
Аналогично,
Теорема доказана
.
Свойство 3. В параллелограмме диагонали точкой пересечения делятся пополам.
Доказательство .
Теорема доказана .
Свойство 4 . Биссектриса угла параллелограмма, пересекая противоположную сторону, делит его на равнобедренный треугольник и трапецию. (Ч. сл. — вершину — два равнобедренных?-ка).
Доказательство
.
Теорема доказана .
Свойство 5 . В параллелограмме отрезок с концами на противоположных сторонах, проходящий через точку пересечения диагоналей, делится этой точкой пополам.
Доказательство .
Теорема доказана .
Свойство 6 . Угол между высотами, опущенными из вершины тупого угла параллелограмма, равен острому углу параллелограмма.
Доказательство .
Теорема доказана .
Свойство 7 . Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.
Доказательство .
Теорема доказана .
Построение биссектрисы угла. Свойства биссектрисы угла треугольника.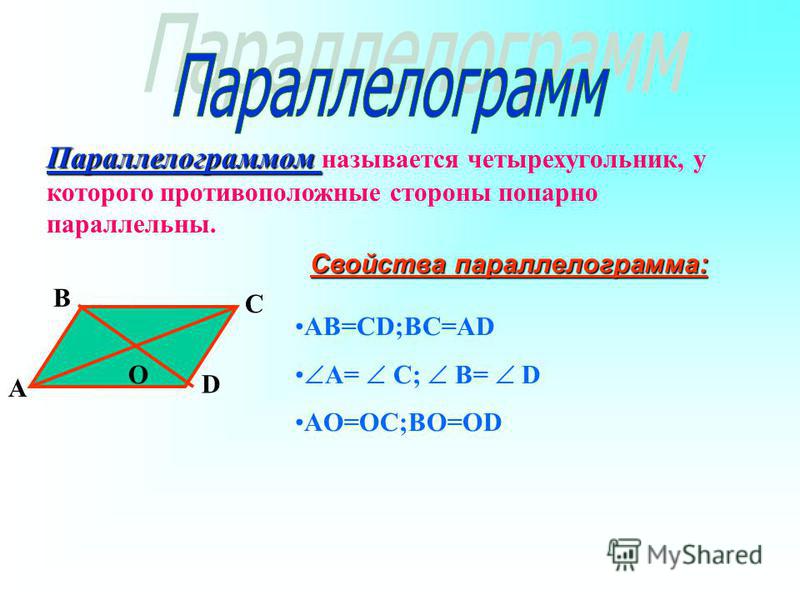
1) Построить произвольный луч DE.
2) На данном луче построить произвольную окружность с центром в вершине и такую же
с центром в начале построенного луча.
3) F и G — точки пересечения окружности со сторонами данного угла, H — точка пересечения окружности с построенным лучом
Построить окружность с центром в точке H и радиусом, равным FG.
5) I — точка пересечения окружностей построенного луча.
6) Провести прямую через вершину и I.
IDH — требуемый угол.
)
Свойство 1 . Биссектриса угла треугольника разбивает противоположную сторону пропорционально прилежащим сторонам.
Доказательство . Пусть x, y-отрезки стороны c. Продолжим луч BC. На луче BC отложим от C отрезок CK, равный AC.
Конспект урока.
Алгебра 8 класс
Учитель Сысой А.К.
Школа 1828
Тема урока: «Параллелограмм и его свойства»
Тип урока: комбинированный
Цели урока:
1) Обеспечить усвоение нового понятия – параллелограмм и его свойств
2) Продолжить развитие навыков и умений решения геометрических задач;
3) Развитие культуры математической речи
План урока:
1. Организационный момент
Организационный момент
(Слайд 1)
На слайде демонстрируется высказывание Льюиса Кэрролла. Ученикам сообщается о цели урока. Проверяется готовность учеников к уроку.
2. Актуализация знаний
(Слайд 2)
На доске задачи для устной работы. Учитель предлагает ученикам подумать над этими задачами и поднять руку тем, кто понял, как задачу решать. После решения двух задач, на доказательство теоремы о сумме углов вызывается к доске ученик, который самостоятельно делает дополнительные построения на чертеже и доказывает устно теорему.
Учениками используется формула суммы углов многоугольника:
3. Основная часть
(Слайд 3)
На доске определение параллелограмма. Учитель говорит о новой фигуре и формулирует определение, делая с помощью чертежа необходимые пояснения. Затем на клетчатой части презентации, с помощью маркера и линейки, показывает, как можно рисовать параллелограмм (возможно несколько случаев)
(Слайд 4)
Учитель формулирует первое свойство параллелограмма. Предлагает ученикам сказать, по рисунку, что дано и что необходимо доказать. После этого на доске появляется дано задачи. Ученики догадываются (может быть при помощи учителя) что искомые равенства надо доказать через равенства треугольников, которые можно получить проведя диагональ (на доске появляется диагональ). Далее ученики догадываются почему треугольники равны и называют признак равенства треугольников (появляется соответствующая форма). Устно сообщают факты, которые необходимы для равенства треугольников (по мере того как они их называют, появляется соответствующая визуализация). Далее ученики формулируют свойство равных треугольников, оно появляется в виде пункта 3 доказательства и затем самостоятельно завершают доказательство теоремы устно.
Предлагает ученикам сказать, по рисунку, что дано и что необходимо доказать. После этого на доске появляется дано задачи. Ученики догадываются (может быть при помощи учителя) что искомые равенства надо доказать через равенства треугольников, которые можно получить проведя диагональ (на доске появляется диагональ). Далее ученики догадываются почему треугольники равны и называют признак равенства треугольников (появляется соответствующая форма). Устно сообщают факты, которые необходимы для равенства треугольников (по мере того как они их называют, появляется соответствующая визуализация). Далее ученики формулируют свойство равных треугольников, оно появляется в виде пункта 3 доказательства и затем самостоятельно завершают доказательство теоремы устно.
(Слайд 5)
Учитель формулирует второе свойство параллелограмма. На доске появляется рисунок параллелограмма. Учитель предлагает по рисунку сказать что дано, что необходимо доказать. После того как ученики правильно сообщают о том, что дано и что необходимо доказать, появляется условие теоремы.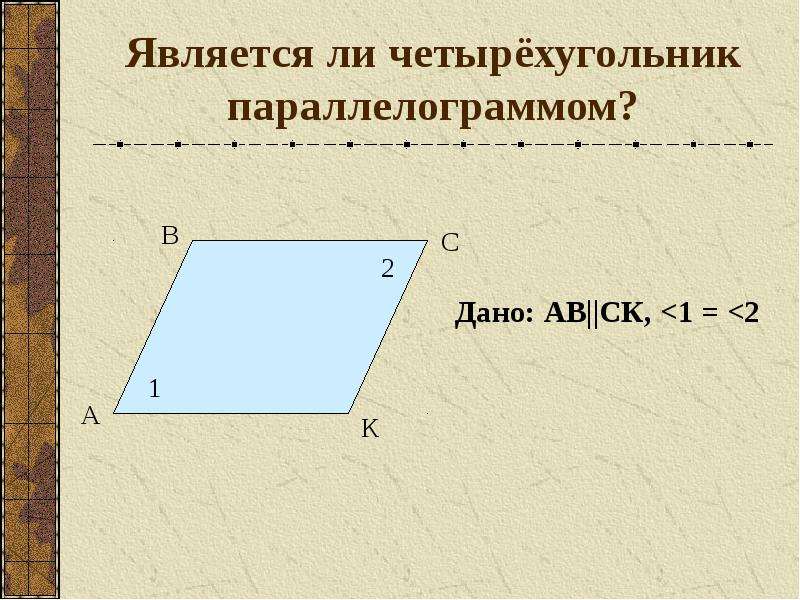 Ученики догадываются, что равенство частей диагоналей можно доказать через равенство треугольников
AOB и
COD . С помощью предыдущего свойства параллелограмма догадываются о равенстве сторон
AB и
CD . Затем понимают, что надо найти равные углы и с помощью свойств параллельных прямых доказывают равенство прилежащих к равным сторонам углов. Данные этапы визуализируются на слайде. Из равенства треугольников следует и истинность теоремы – проговаривают ученики на слайде появляется соответствующая визуализация.
Ученики догадываются, что равенство частей диагоналей можно доказать через равенство треугольников
AOB и
COD . С помощью предыдущего свойства параллелограмма догадываются о равенстве сторон
AB и
CD . Затем понимают, что надо найти равные углы и с помощью свойств параллельных прямых доказывают равенство прилежащих к равным сторонам углов. Данные этапы визуализируются на слайде. Из равенства треугольников следует и истинность теоремы – проговаривают ученики на слайде появляется соответствующая визуализация.
(Слайд 6)
Учитель формулирует третье свойство параллелограмма. В зависимости от времени, которое остаётся до конца урока, учитель может дать возможность ученикам самостоятельно доказать это свойство, или ограничится его формулировкой, а само доказательство оставить ученикам в качестве домашней работы. Доказательство может опираться на сумму углов вписанного многоугольника, которая повторялась в начале урока, или на сумму внутренних односторонних углов при двух параллельных прямых
AD и
BC , и секущей, например
AB .
4. Закрепление материала
На этом этапе учащиеся, используя ранее изученные теоремы, решают задачи. Идеи к решению задачи подбирают ученики самостоятельно. Так как возможных вариантов оформления немало и все они зависят от того каким образом ученики будут искать решение задачи, визуализации решения задач нет, а ученики самостоятельно оформляют каждый этап решения на отдельной доске с записью решения в тетрадь.
(Слайд 7)
Появляется условие задачи. Учитель предлагает по условию сформулировать «Дано». После того, как ученики, верно составят краткую запись условия на доске появляется «Дано». Ход решения задачи может выглядеть следующим образом:
Проведём высоту BH (визуализировано)
Треугольник AHB – прямоугольный. Угол A равен углу C и равен 30 0 (по свойству о противоположных углах в параллелограмме). 2BH =AB (по свойству катета, лежащего напротив угла в 30 0 в прямоугольном треугольнике). Значит AB = 13 см.
AB
= CD
, BC
= AD
(по свойству противоположных сторон в параллелограмме) Значит AB
=CD
=13см. Так как периметр параллелограмма равен 50 см, то BC
=AD
=(50 – 26):2=12см.
Так как периметр параллелограмма равен 50 см, то BC
=AD
=(50 – 26):2=12см.
Ответ: AB = CD = 13 см, BC = AD = 12 см.
(Слайд 8)
Появляется условие задачи. Учитель предлагает по условию сформулировать «Дано». После появляется «Дано» на экране. С помощью красных линий выделяется четырёхугольник, про который нужно доказать, что он параллелограмм. Ход решения задачи может выглядеть следующим образом:
Т.к. BK и MD перпендикуляры к одной прямой, то прямы BK и MD параллельны.
Через смежные углы можно показать, что сумма внутренних односторонних углов при прямых BM и KD и секущей MD равна 180 0 . Поэтому данные прямые параллельны.
Так как у четырехугольника BMDK противоположные стороны попарно параллельны, то данный четырехугольник параллелограмм.
5. Окончание урока. Поведение итогов.
(Слайд 8)
На слайде появляются вопросы по новой теме, на которые ученики отвечают.
Для того, чтобы определить является ли данная фигура параллелограммом существует ряд признаков.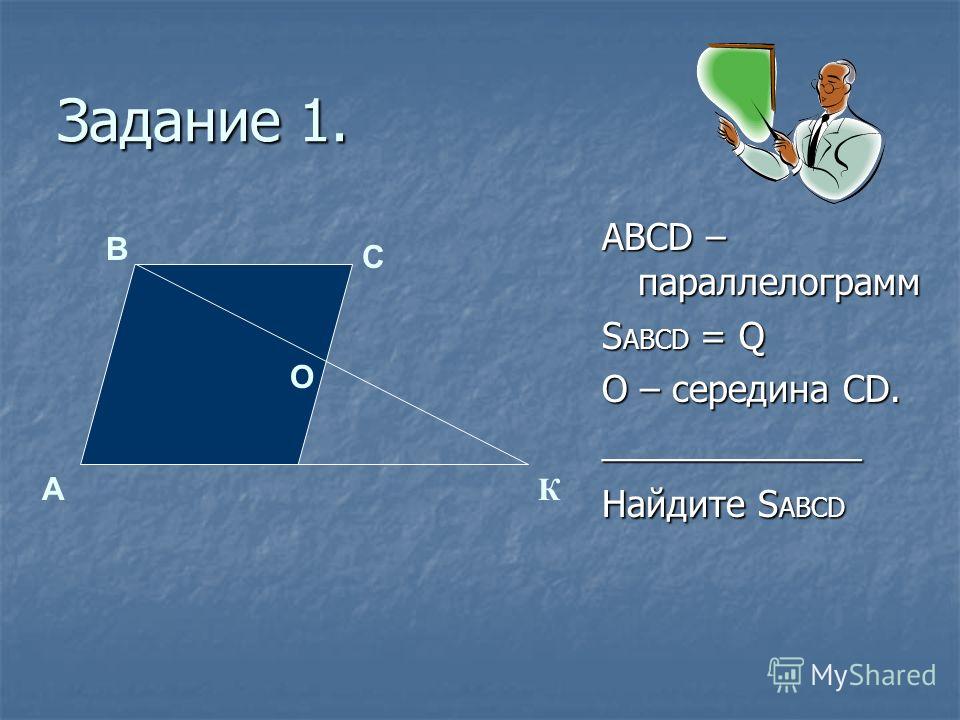 Рассмотрим три основных признака параллелограмма.
Рассмотрим три основных признака параллелограмма.
1 признак параллелограмма
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник будет являться параллелограммом.
Доказательство:
Рассмотрим четырехугольник ABCD. Пусть в нем стороны AB и СD параллельны. И пусть AB=CD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.
Эти треугольники равны между собой по двум сторонам и углу между ними (BD — общая сторона, AB = CD по условию, угол1 = угол2 как накрест лежащие углы при секущей BD параллельных прямых AB и CD.), а следовательно угол3 = угол4.
А эти углы будут являться накрест лежащими при пересечении прямых BC и AD секущей BD. Из этого следует что BC и AD параллельны между собой. Имеем, что в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD является параллелограммом.
2 признак параллелограмма
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник будет параллелограммом.
Доказательство:
Рассмотрим четырехугольник ABCD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.
Эти два треугольника буду равны между собой по трем сторонам (BD — общая сторона, AB = CD и BC = AD по условию). Из этого можно сделать вывод, что угол1 = угол2. Отсюда следует, что AB параллельна CD. А так как AB = CD и AB параллельна CD, то по первому признаку параллелограмма, четырехугольник ABCD будет являться параллелограммом.
3 признак параллелограмма
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник будет являться параллелограммом.
Рассмотрим четырехугольник ABCD. Проведем в нем две диагонали AC и BD, которые будут пересекаться в точке О и делятся этой точкой пополам.
Треугольники AOB и COD будут равны между собой, по первому признаку равенства треугольников. (AO = OC, BO = OD по условию, угол AOB = угол COD как вертикальные углы. ) Следовательно, AB = CD и угол1 = угол 2. Из равенства углов 1 и 2 имеем, что AB параллельна CD. Тогда имеем, что в четырехугольнике ABCD стороны AB равны CD и параллельны, и по первому признаку параллелограмма четырехугольник ABCD будет являться параллелограммом.
) Следовательно, AB = CD и угол1 = угол 2. Из равенства углов 1 и 2 имеем, что AB параллельна CD. Тогда имеем, что в четырехугольнике ABCD стороны AB равны CD и параллельны, и по первому признаку параллелограмма четырехугольник ABCD будет являться параллелограммом.
Параллелограмм делится на равные треугольники. Определение параллелограма и его свойства. Диагонали разделены пополам точкой пересечения
1. Определение параллелограмма.
Если пару параллельных прямых пересечём другой парой параллельных прямых, то получим четырёхугольник, у которого противоположные стороны попарно параллельны.
В четырёхугольниках ABDС и ЕFNМ (рис. 224) ВD || АС и AB || СD;
ЕF || МN и ЕМ || FN.
Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
2. Свойства параллелограмма.
Теорема
. Диагональ параллелограмма делит его на два равных треугольника.
Пусть имеется параллелограмм ABDС (рис. 225), в котором AB || СD и АС || ВD.
Требуется доказать, что диагональ делит его на два равных треугольника.
Проведём в параллелограмме ABDС диагональ СВ. Докажем, что \(\Delta\)CAB = \(\Delta\)СDВ.
Сторона СВ общая для этих треугольников; ∠ABC = ∠BCD, как внутренние накрест лежащие углы при параллельных AB и СD и секущей СВ; ∠ACB = ∠СВD, тоже как внутренние накрест лежащие углы при параллельных АС и ВD и секущей CB.
Отсюда \(\Delta\)CAB = \(\Delta\)СDВ.
Таким же путём можно доказать, что диагональ AD разделит параллелограмм на два равных треугольника АСD и ABD.
Следствия:
1 . Противоположные углы параллелограмма равны между собой.
∠А = ∠D, это следует из равенства треугольников CAB и СDВ.
Аналогично и ∠С = ∠В.
2. Противоположные стороны параллелограмма равны между собой.
AB = СD и АС = ВD, так как это стороны равных треугольников и лежат против равных углов.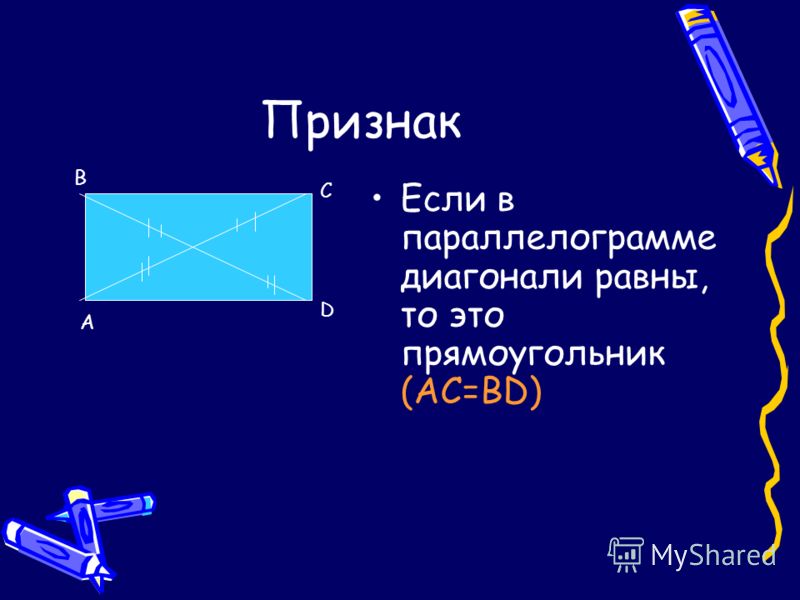
Теорема 2. Диагонали параллелограмма в точке их пересечения делятся пополам.
Пусть BC и AD — диагонали параллелограмма AВDС (рис. 226). Докажем, что АО = OD и СО = OB.
Для этого сравним какую-нибудь пару противоположно расположенных треугольников, например \(\Delta\)AOB и \(\Delta\)СОD.
В этих треугольниках AB = СD, как противоположные стороны параллелограмма;
∠1 = ∠2, как углы внутренние накрест лежащие при параллельных AB и СD и секущей AD;
∠3 = ∠4 по той же причине, так как AB || СD и СВ — их секущая.
Отсюда следует, что \(\Delta\)AOB = \(\Delta\)СОD. А в равных треугольниках против равных углов лежат равные стороны. Следовательно, АО = OD и СО = OB.
Теорема 3. Сумма углов, прилежащих к одной стороне параллелограмма, равна 180° .
В параллелограмме ABCD проведем диагональ АС и получим два треугольника ABC и ADC.
Треугольники равны, так как ∠1 = ∠4, ∠2 = ∠3 (накрест лежащие углы при параллельных прямых), а сторона АС общая.
Из равенства \(\Delta\)ABC = \(\Delta\)ADC следует, что AB = CD, BC = AD, ∠B = ∠D.
Сумма углов, прилежащих к одной стороне, например углов А и D, равна 180° как односторонних при параллельных прямых.
Трапеция — это четырёхугольник, у которого две противоположные стороны параллельны (рис.36).
Здесь AD || BC. Параллельные стороны называются основаниями трапеции, а две другие (AB и CD) – боковыми сторонами. Расстояние между основаниями (BM) есть высота. Отрезок EF, соединяющий средние точки E и F боковых сторон, называется средней линией трапеции. Средняя линия трапеции равна полусумме оснований:
и параллельна им: EF || AD и EF || BC.
Трапеция с равными боковыми сторонами (AB = CD) называется равнобочной трапецией. В равнобочной трапеции углы при каждом основании равны (A = D, B = C).
Параллелограмм (ABCD, рис.32) – это четырёхугольник, противоположные стороны которого попарно параллельны.
Любые две противоположные стороны параллелограмма называются его основаниями, а расстояние между ними – высотой (BE, рис.
 32).
32).Свойства параллелограмма.
1. Противоположные стороны параллелограмма равны (AB = CD, AD = BC).
2. Противоположные углы параллелограмма равны (A = C, B = D).
Сумма углов параллелограмма, прилежащих к одной его стороне составляет 180°. Например, A+ B=180°.
3. Диагонали параллелограмма делятся в точке их пересечения пополам (AO = OC, BO = OD).
4.Любая диагональ параллелограмма делит его на два равных треугольника. Δ ABD=Δ BCD.
5. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его четырёх сторон: AC² + BD² = AB² + BC² + CD² + AD² .
Признаки параллелограмма.
Четырёхугольник является параллелограммом, если выполняется одно из следующих условий:
1. Противоположные стороны попарно равны (AB = CD, AD = BC).
2. Противоположные углы попарно равны (A = C, B = D).
3. Две противоположные стороны равны и параллельны (AB = CD, AB || CD).
4. Диагонали делятся в точке их пересечения пополам (AO = OC, BO = OD).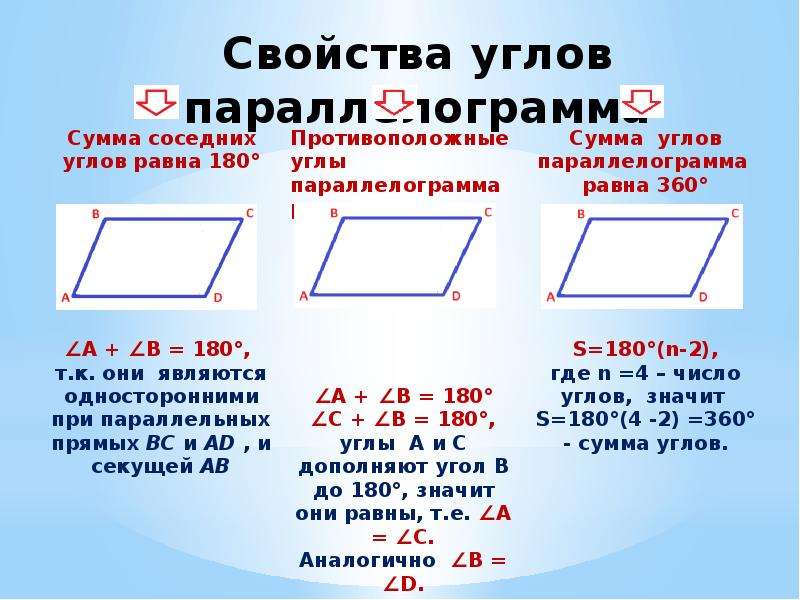
Плоская фигура, образованная замкнутой цепочкой отрезков, называется многоугольником. В зависимости от количества углов многоугольник может быть треугольником, четырёхугольником, пятиугольником, шестиугольником и т.д. На рис.17 показан шестиугольник ABCDEF.
Точки А, В, C, D, E, F – вершины многоугольника; углы A , B , C , D, E , F – углы многоугольника; отрезки AC, AD, BE и т.д. — диагонали; AB, BC, CD, DE, EF, FA – стороны многоугольника; сумма длин сторон AB + BC + … + FA называется периметром и обозначается p (иногда обозначают – 2p, тогда p – полупериметр). В элементарной геометрии рассматриваются только простые многоугольники, контуры которых не имеют самопересечений, как показано на рис.18. Если все диагонали лежат внутри многоугольника, он называется выпуклым. Шестиугольник на рис.17 выпуклый; пятиугольник ABCDE на рис.19 не выпуклый, так как его диагональ AD лежит снаружи. Сумма внутренних углов выпуклого многоугольника равна 180º (n – 2), где n — число углов (или сторон) многоугольника.
Определение
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема (первый признак параллелограмма)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Доказательство
Пусть в четырехугольнике \(ABCD\) стороны \(AB\) и \(CD\) параллельны и \(AB = CD\) .
Проведём диагональ \(AC\)
, разделяющую данный четырехугольник на два равных треугольника: \(ABC\)
и \(CDA\)
. Эти треугольники равны по двум сторонам и углу между ними (\(AC\)
– общая сторона, \(AB = CD\)
по условию, \(\angle 1 = \angle 2\)
как накрест лежащие углы при пересечении параллельных прямых \(AB\)
и \(CD\)
секущей \(AC\)
), поэтому \(\angle 3 = \angle 4\)
. Но углы \(3\)
и \(4\)
накрест лежащие при пересечении прямых \(AD\)
и \(BC\)
секущей \(AC\)
, следовательно, \(AD\parallel BC\)
. Таким образом, в четырехугольнике \(ABCD\)
противоположные стороны попарно параллельны, и, значит, четырехугольник \(ABCD\)
– параллелограмм.
Теорема (второй признак параллелограмма)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Проведём диагональ \(AC\) данного четырехугольника \(ABCD\) , разделяющую его на треугольники \(ABC\) и \(CDA\) .
Эти треугольники равны по трем сторонам (\(AC\) – общая, \(AB = CD\) и \(BC = DA\) по условию), поэтому \(\angle 1 = \angle 2\) – накрест лежащие при \(AB\) и \(CD\) и секущей \(AC\) . Отсюда следует, что \(AB\parallel CD\) . Так как \(AB = CD\) и \(AB\parallel CD\) , то по первому признаку параллелограмма четырёхугольник \(ABCD\) – параллелограмм.
Теорема (третий признак параллелограмма)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство
Рассмотрим четырехугольник \(ABCD\)
, в котором диагонали \(AC\)
и \(BD\)
пересекаются в точке \(O\)
и делятся этой точкой пополам.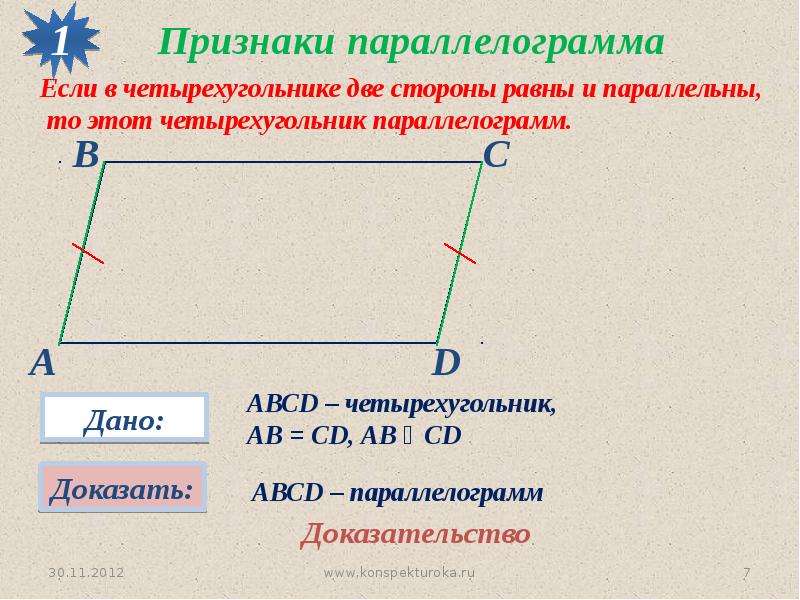
Треугольники \(AOB\) и \(COD\) равны по первому признаку равенства треугольников (\(AO = OC\) , \(BO = OD\) по условию, \(\angle AOB = \angle COD\) как вертикальные углы), поэтому \(AB = CD\) и \(\angle 1 = \angle 2\) . Из равенства углов \(1\) и \(2\) (накрест лежащие при \(AB\) и \(CD\) и секущей \(AC\) ) следует, что \(AB\parallel CD\) .
Итак, в четырехугольнике \(ABCD\) стороны \(AB\) и \(CD\) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник \(ABCD\) – параллелограмм.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Свойства биссектрисы параллелограмма:
1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.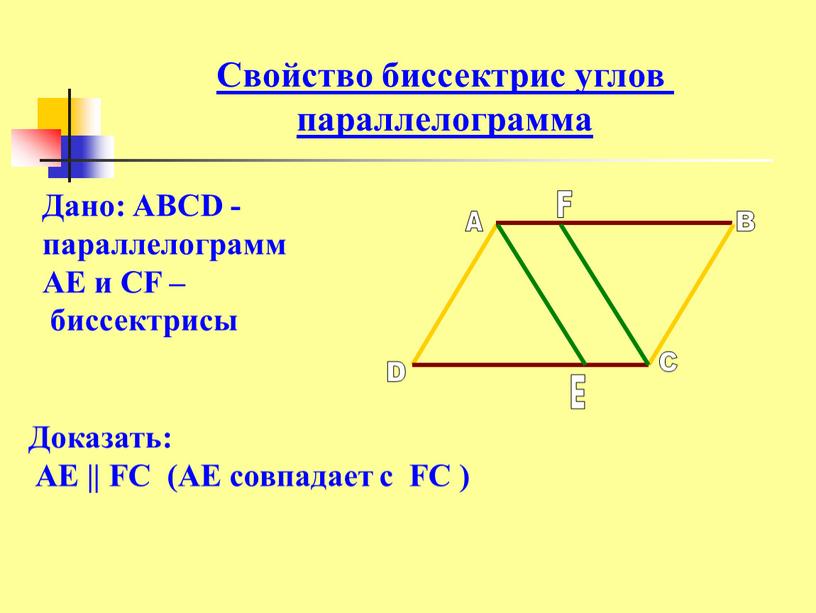 \circ\)
.
\circ\)
.
3. Пусть \(AN\) и \(CM\) – биссектрисы углов параллелограмма \(ABCD\) .
Так как в параллелограмме противоположные углы равны, то \(\angle 2 = 0,5\cdot\angle BAD = 0,5\cdot\angle BCD = \angle 1\) . Кроме того, углы \(1\) и \(3\) равны как накрест лежащие при параллельных прямых \(AD\) и \(BC\) и секущей \(CM\) , тогда \(\angle 2 = \angle 3\) , откуда следует, что \(AN\parallel CM\) . Кроме того, \(AM\parallel CN\) , тогда \(ANCM\) – параллелограмм, следовательно, \(AN = CM\) .
Доказательство
Первым делом проведем диагональ AC . Получаются два треугольника: ABC и ADC .
Так как ABCD — параллелограмм, то справедливо следующее:
AD || BC \Rightarrow \angle 1 = \angle 2 как лежащие накрест.
AB || CD \Rightarrow \angle3 = \angle 4 как лежащие накрест.
Следовательно, \triangle ABC = \triangle ADC (по второму признаку: и AC — общая).
И, значит, \triangle ABC = \triangle ADC
, то AB = CD
и AD = BC
.
Доказано!
2. Противоположные углы тождественны.
Доказательство
Согласно доказательству свойства 1 мы знаем, что \angle 1 = \angle 2, \angle 3 = \angle 4 . Таким образом сумма противоположных углов равна: \angle 1 + \angle 3 = \angle 2 + \angle 4 . Учитывая, что \triangle ABC = \triangle ADC получаем \angle A = \angle C , \angle B = \angle D .
Доказано!
3. Диагонали разделены пополам точкой пересечения.
Доказательство
Проведем еще одну диагональ.
По свойству 1 мы знаем, что противоположные стороны тождественны: AB = CD . Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что \triangle AOB = \triangle COD по второму признаку равенства треугольников (два угла и сторона между ними). То есть, BO = OD (напротив углов \angle 2 и \angle 1 ) и AO = OC (напротив углов \angle 3 и \angle 4 соответственно).
Доказано!
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?» . То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.
AB = CD ; AB || CD \Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим подробнее. Почему AD || BC ?
\triangle ABC = \triangle ADC по свойству 1 : AB = CD , AC — общая и \angle 1 = \angle 2 как накрест лежащие при параллельных AB и CD и секущей AC .
Но если \triangle ABC = \triangle ADC , то \angle 3 = \angle 4 (лежат напротив AB и CD соответственно). И следовательно AD || BC (\angle 3 и \angle 4 — накрест лежащие тоже равны).
Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны.
AB = CD
, AD = BC \Rightarrow ABCD
— параллелограмм. {\circ}
говорит и о том, что AD || BC
.
{\circ}
говорит и о том, что AD || BC
.
При этом \alpha и \beta — внутренние односторонние при секущей AD . И это значит AB || CD .
Третий признак верен.
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам.
AO = OC ; BO = OD \Rightarrow параллелограмм.
Доказательство
BO = OD ; AO = OC , \angle 1 = \angle 2 как вертикальные \Rightarrow \triangle AOB = \triangle COD , \Rightarrow \angle 3 = \angle 4 , и \Rightarrow AB || CD .
Аналогично BO = OD ; AO = OC , \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8 , и \Rightarrow AD || BC .
Четвертый признак верен.
Как найти площадь параллелограммаСупер русские картинки
- Сортировать по:
- дате
- просмотрам
- популярности
Площадь параллелограмма через диагонали.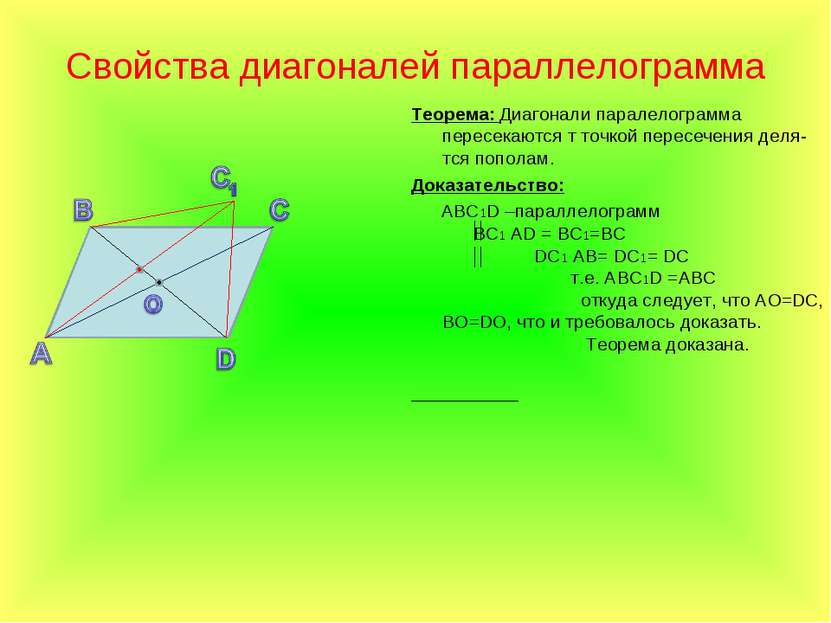 Формула площади параллелограмма через диагонали позволяет быстро найти значение. Для вычислений понадобится величина угла, расположенного между диагоналями. Рассмотрим пример расчета площади параллелограмма через диагонали. Площадь параллелограмма равна произведению его основания (a) на высоту (h): \[S=a h\] (a — основание параллелограмма; h — высота параллелограмма) Подведём итоги по всему вышесказанному, площадь параллелограмма составит: S = 2 3 − 5 6 = 12 + 15 = 3 3. Пример 3 Даны векторы a → = 3 i – j + k; b → = 5 i. Формула для нахождения площади параллелограмма через стороны и угол между ними: S = a ⋅ b ⋅ sin ( α) {S= a \cdot b \cdot \sin ( {\alpha})} S = a ⋅ b ⋅ sin(α), где a и b — стороны параллелограмма, α — угол между сторонами. Как найти площадь параллелограмма — простой и понятный онлайн калькулятор, плюс немного теории. Чтобы понять, как найти площадь параллелограмма, построенного на векторах, следует подробнее изучить эту фигуру. Формула нахождения площади параллелограммы выглядит следующим образом:S = a * Ha,где a – сторона;Ha – длина диагонали, проведенной к стороне a.
Формула площади параллелограмма через диагонали позволяет быстро найти значение. Для вычислений понадобится величина угла, расположенного между диагоналями. Рассмотрим пример расчета площади параллелограмма через диагонали. Площадь параллелограмма равна произведению его основания (a) на высоту (h): \[S=a h\] (a — основание параллелограмма; h — высота параллелограмма) Подведём итоги по всему вышесказанному, площадь параллелограмма составит: S = 2 3 − 5 6 = 12 + 15 = 3 3. Пример 3 Даны векторы a → = 3 i – j + k; b → = 5 i. Формула для нахождения площади параллелограмма через стороны и угол между ними: S = a ⋅ b ⋅ sin ( α) {S= a \cdot b \cdot \sin ( {\alpha})} S = a ⋅ b ⋅ sin(α), где a и b — стороны параллелограмма, α — угол между сторонами. Как найти площадь параллелограмма — простой и понятный онлайн калькулятор, плюс немного теории. Чтобы понять, как найти площадь параллелограмма, построенного на векторах, следует подробнее изучить эту фигуру. Формула нахождения площади параллелограммы выглядит следующим образом:S = a * Ha,где a – сторона;Ha – длина диагонали, проведенной к стороне a. Если неизвестна высота – вторая необходимая величина, возьмите за основу одну из сторон и проведите к ней высоту, которую предстоит найти. Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними. Хорошо, когда по условиям даны длины этих самых векторов. Формула площади через стороны и углы параллелограмма, ( S ): Калькулятор — вычислить, найти площадь параллелограмма: a (сторона)=. b (сторона)=. α или β (угол в градусах)= ( sin α=sin β ) S =. 2. Формула площади параллелограмма через сторону и высоту. a, b — стороны параллелограмма. В задачах по геометрии, точнее по планиметрии и тригонометрии, иногда требуется найти высоту параллелограмма, исходя из заданных значений сторон, углов, диагоналей и т.п.
Если неизвестна высота – вторая необходимая величина, возьмите за основу одну из сторон и проведите к ней высоту, которую предстоит найти. Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними. Хорошо, когда по условиям даны длины этих самых векторов. Формула площади через стороны и углы параллелограмма, ( S ): Калькулятор — вычислить, найти площадь параллелограмма: a (сторона)=. b (сторона)=. α или β (угол в градусах)= ( sin α=sin β ) S =. 2. Формула площади параллелограмма через сторону и высоту. a, b — стороны параллелограмма. В задачах по геометрии, точнее по планиметрии и тригонометрии, иногда требуется найти высоту параллелограмма, исходя из заданных значений сторон, углов, диагоналей и т.п.
hmr6ua.rustoy78.ru
http://4pk817.masmat.ru
http://w659oo.obzorkurs.ru
http://ksyg8x.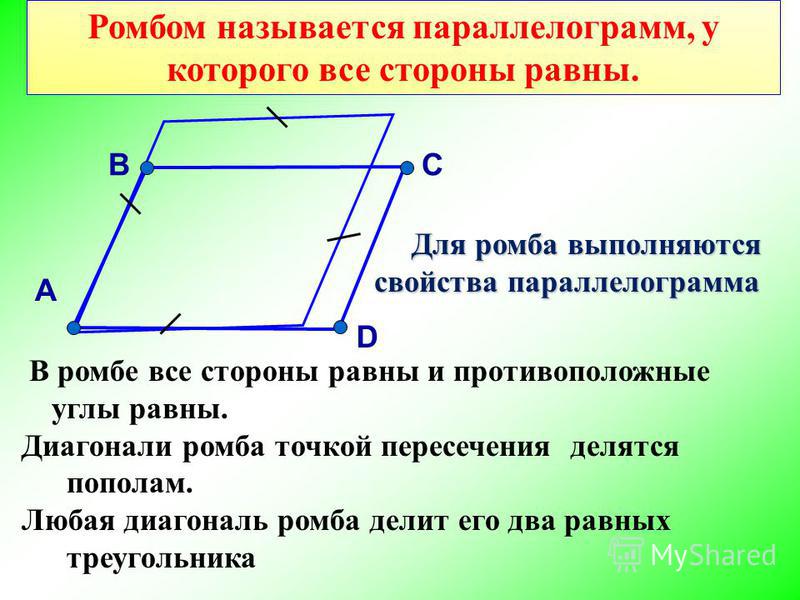 vulcan-sloty.ru
4slws9.kara-bass
vulcan-sloty.ru
4slws9.kara-bass
Популярные картинки от http://bmtproject.ru/
как нарисовать маму поэтапноновелла этоватсап на пк без телефонафокусировка вниманиясколопендра артплощадь неправильного четырехугольникараскраска фнафпухлый человеккак сделать фон прозрачным в фотошопестих папе на день рождениякак найти площадь параллелограммафон на рабочий стол анименаписать стих,сказку или фантастичный рассказ на тему «давление в нашей жизни»(_)Люди пажалуйста я ужасный поэт,напишите хоть чт
Нет, так как сопротивление амперметра мало
Ядерная реакция – это процесс взаимодействия атомного ядра с другим ядром или элементарной частицей, сопровождающийся изменением состава и структуры ядра и выделением вторичных частиц или γ-квантов.
Альфа распад- превращение атомных ядер, сопровождаемое испусканием альфа частиц
Бетта распад- радиоактивные ядра могут выбрасывать поток электронов, которые порождаются в результате превращения нейтронов в протоны.
Правило сдвига: сумма массовых чисел всех ядер и частиц в левой части уравнения будет равна сумме массовых чисел ядер и частиц в правой части уравнения.
Если сумма масс ядер и частиц, вступивших в реакцию, больше суммы масс ядер и частиц, возникающих в результате реакции, то будет выделение энергии, если меньше- поглощение энергии.
Ответ под пунктом три , но а еще точнее ответ -273,15 С
880 м/сек*0,98н=34,3н*v
v= 880*0.98/34.3=25,14 м/сек
Скорость отдачи винтовки 25,14 м/сек
По уравнению Менделеева клайперона p1V=vRT1, v=(p1V/RT1)
p2V=vRT2, p2=vRT2/V=p1T2/T1.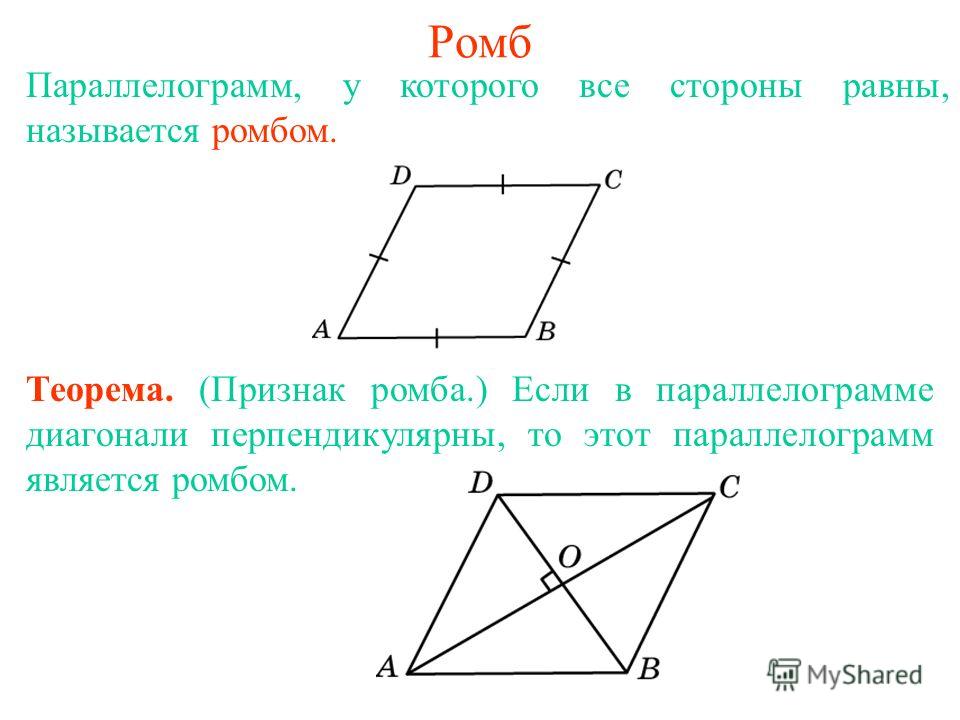 Или это изохорный процесс, объем не изменяется, по закону Шарля p1/T1 = p2/T2, p2=p1T2/T1
Или это изохорный процесс, объем не изменяется, по закону Шарля p1/T1 = p2/T2, p2=p1T2/T1
Шесть свойств параллелограмма
Параллелограммы — это четырехсторонние формы с двумя парами параллельных сторон. Прямоугольники, квадраты и ромбы классифицируются как параллелограммы. Классический параллелограмм выглядит как наклонный прямоугольник, но любую четырехстороннюю фигуру, имеющую параллельные и совпадающие пары сторон, можно классифицировать как параллелограмм. Параллелограммы имеют шесть основных свойств, которые отличают их от других форм.
Противоположные стороны конгруэнтны
Противоположные стороны всех параллелограммов, включая прямоугольники и квадраты, должны быть конгруэнтными.Для параллелограмма ABCD, если сторона AB находится на вершине параллелограмма и составляет 9 сантиметров, сторона CD внизу параллелограмма также должна быть 9 сантиметров.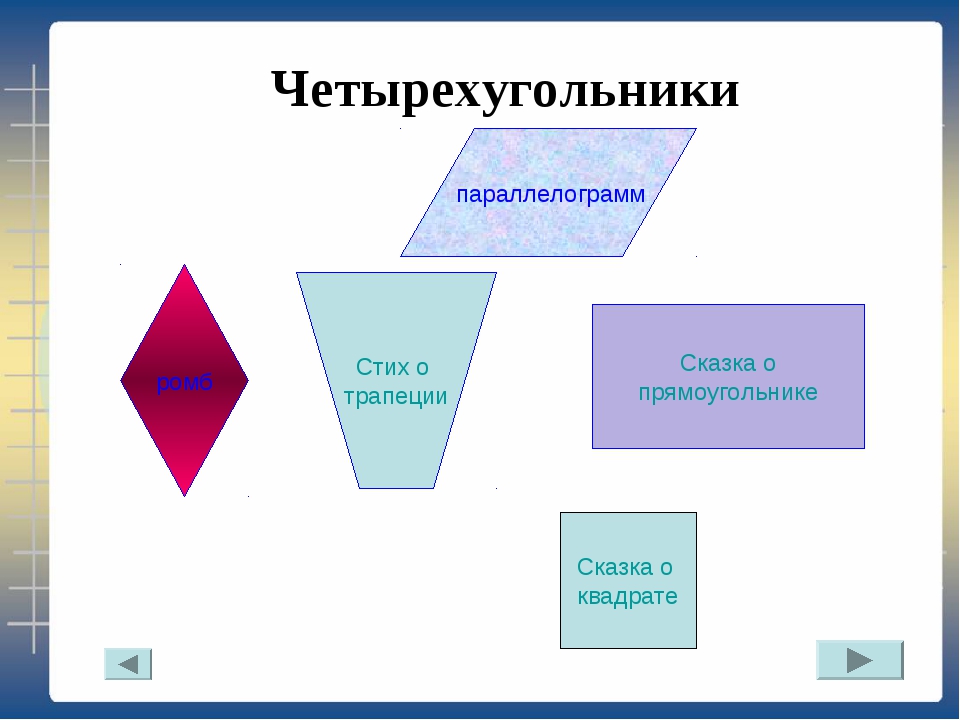 Это также верно для другого набора сторон; если сторона AC составляет 12 сантиметров, сторона BD, противоположная AC, также должна быть 12 сантиметров.
Это также верно для другого набора сторон; если сторона AC составляет 12 сантиметров, сторона BD, противоположная AC, также должна быть 12 сантиметров.
Противоположные углы конгруэнтны
Противоположные углы всех параллелограммов, включая квадраты и прямоугольники, должны быть конгруэнтными. В параллелограмме ABCD, если углы B и C расположены в противоположных углах, а угол B равен 60 градусам, угол C также должен быть 60 градусов.Если угол А равен 120 градусам — угол D, противоположный углу А, тоже должен быть 120 градусов.
Дополнительные углы
Дополнительные углы — это пара из двух углов, сумма которых составляет 180 градусов. Для параллелограмма ABCD, приведенного выше, углы B и C противоположны и составляют 60 градусов. Следовательно, угол A, который следует за углами B и C, должен составлять 120 градусов (120 + 60 = 180). Угол D, который также следует за углами B и C, также составляет 120 градусов. Кроме того, это свойство поддерживает правило, согласно которому противоположные углы должны быть конгруэнтными, поскольку углы A и D считаются конгруэнтными.
Кроме того, это свойство поддерживает правило, согласно которому противоположные углы должны быть конгруэнтными, поскольку углы A и D считаются конгруэнтными.
Прямые углы в параллелограммах
Хотя учащихся учат, что четырехсторонние фигуры с прямыми углами — 90 градусов — являются квадратами или прямоугольниками, они также являются параллелограммами, но с четырьмя равными углами вместо двух пар из двух равных углов . В параллелограмме, если один из углов является прямым, все четыре угла должны быть прямыми углами.Если у четырехгранной фигуры один прямой угол и хотя бы один угол другой меры, это не параллелограмм; это трапеция.
Диагонали в параллелограммах
Диагонали параллелограмма проводятся от одной противоположной стороны параллелограмма к другой. В параллелограмме ABCD это означает, что одна диагональ проводится от вершины A к вершине D, а другая — от вершины B к вершине C. Рисуя диагонали, учащиеся обнаруживают, что они делят друг друга пополам или пересекаются в своих средних точках.Это происходит потому, что противоположные углы параллелограмма совпадают. Сами диагонали не будут совпадать друг с другом, если параллелограмм также не является квадратом или ромбом.
Рисуя диагонали, учащиеся обнаруживают, что они делят друг друга пополам или пересекаются в своих средних точках.Это происходит потому, что противоположные углы параллелограмма совпадают. Сами диагонали не будут совпадать друг с другом, если параллелограмм также не является квадратом или ромбом.
Конгруэнтные треугольники
Если в параллелограмме ABCD провести диагональ от вершины A к вершине D, будут созданы два конгруэнтных треугольника, ACD и ABD. Это также верно при рисовании диагонали от вершины B к вершине C. Создаются еще два конгруэнтных треугольника, ABC и BCD. Когда обе диагонали нарисованы, создаются четыре треугольника, каждый со средней точкой E.Однако эти четыре треугольника конгруэнтны, только если параллелограмм является квадратом.
Разница между параллелограммом и прямоугольником
Geometry обращается к классификации форм и фигур, которую также можно описать как пространственную ориентацию объекта. Существует множество различных геометрических форм, включая двухмерные четырехугольники.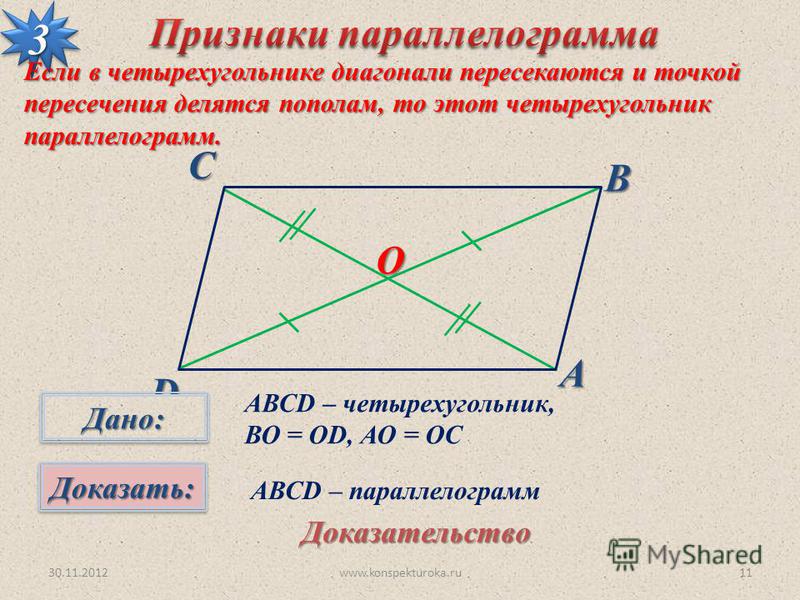 Это относится ко всем четырехсторонним геометрическим формам, которые далее делятся на четыре категории, а именно трапеции, равнобедренные трапеции, воздушные змеи и параллелограммы.Все это простые формы, которые не пересекаются между собой и представляют собой область, ограниченную четырьмя сторонами.
Это относится ко всем четырехсторонним геометрическим формам, которые далее делятся на четыре категории, а именно трапеции, равнобедренные трапеции, воздушные змеи и параллелограммы.Все это простые формы, которые не пересекаются между собой и представляют собой область, ограниченную четырьмя сторонами.
Что такое параллелограмм?
Параллелограмм классифицируется как замкнутая четырехугольная фигура с конгруэнтными или подобными противоположными сторонами, которые параллельны, также известный как четырехугольник. Две параллельные стороны известны как основания параллелограмма, а расстояние между парой называется высотой. Площадь параллелограмма может быть описана как (1/2) h (2 b ), или, скорее, bh , где h — высота, а b — основание.Еще одна особенность, отличающая параллелограммы, — это две пары параллельных линий. Диагонали — еще одна особенность, которую следует учитывать; при рисовании между противоположными углами линии точно пересекают друг друга. Каждая из этих диагоналей имеет тенденцию делить параллелограмм на два равных треугольника, а пересечение обеих диагоналей делит его на четыре треугольника, при этом противоположные треугольники равны. Когда складываются квадраты сторон, получается сумма диагоналей. Параллелограмм также имеет дополнительные смежные углы.
Каждая из этих диагоналей имеет тенденцию делить параллелограмм на два равных треугольника, а пересечение обеих диагоналей делит его на четыре треугольника, при этом противоположные треугольники равны. Когда складываются квадраты сторон, получается сумма диагоналей. Параллелограмм также имеет дополнительные смежные углы.
Что такое прямоугольник?
Прямоугольник часто описывают как частный случай параллелограмма, так как он имеет аналогичные свойства, но высота равна высоте одной из параллельных сторон. Это означает, что формула для прямоугольника: lw ( длина, x ширина) вместо bh. Прямоугольник также имеет две противоположные параллельные стороны, хотя у него также есть перпендикулярные последовательные стороны, что означает, что противоположные углы всегда равны 90 °.Диагонали всегда делят друг друга пополам и в результате получаются отрезки одинаковой длины. Другими словами, параллелограмм с равными противоположными сторонами и углами 90 ° называется прямоугольником.
Параллелограмм Vs. Прямоугольник
1. Классификация
Это оба четырехугольника, причем прямоугольник классифицируется как разновидность параллелограмма. У параллелограммов и прямоугольников два набора параллельных сторон, хотя у прямоугольника есть следующие друг за другом стороны, перпендикулярные.
2. Уголки
Противоположные внутренние углы параллелограмма и прямоугольника эквивалентны. Основное отличие состоит в том, что прямоугольник всегда имеет углы 90 °, в то время как у параллелограмма угол может меняться. Другими словами, углы прямоугольника всегда равны или равноугольны.
3. Диагонали
В случае параллелограмма диагонали не равны, и он делит форму пополам на два равных треугольника. Прямоугольник имеет равные диагонали, что делит прямоугольник пополам на два равных прямоугольных треугольника.
4 . Формулы Формула для вычисления площади параллелограммов: bh (ширина x высота ), а площадь прямоугольника рассчитывается как lw (длина x ширина ).
Существует «закон параллелограмма», который применяется к параллелограммам, где сумма квадратов всех сторон эквивалентна сумме квадратов диагоналей. Прямоугольники, с другой стороны, подчиняются «закону Пифагора», где сумма квадратов двух смежных сторон равна квадрату диагонали.
Параллелограмм и прямоугольник: сравнительная таблица
Резюме параллелограмма Vs. Прямоугольник
Есть определенные критерии, по которым четырехугольник можно определить как параллелограмм. Наиболее очевидным является наличие двух пар параллельных сторон. Прямоугольник известен как частный случай параллелограмма, поскольку он соответствует основной классификации параллелограмма, но имеет особенности, которые его отличают. Это включает в себя противоположные стороны равной длины, пересекающиеся под углом 90 ° во всех случаях.Таким образом, диагонали равны и делит прямоугольник на прямоугольные треугольники, тогда как диагонали параллелограмма не равны и делят его пополам на два равных треугольника с углами, зависящими от угла параллелограмма.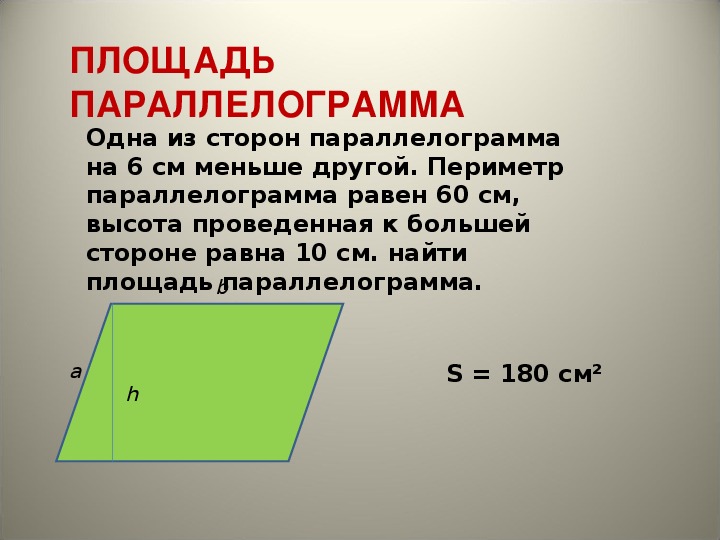
: Если вам понравилась эта статья или наш сайт. Пожалуйста, поделитесь информацией. Поделитесь им с друзьями / семьей.
Cite
Mardi Stratuss. «Разница между параллелограммом и прямоугольником.«DifferenceBetween.net. 4 октября 2019 года.
Аран Фауддви, горы Риног и заимствованная концепция ‘Аран миль’ Аран Фауддви (Aran Fawddwy) — самая высокая гора в группе Аран на юго-востоке Сноудонии, Уэльс. Ее высота составляет 907 метров / 2975 футов, это самая высокая гора в Уэльсе, не достигающая 3000 футов. В соответствии с горами Риног, соседними с Аранами, и видимыми вдоль хребта от Глазгвма до вершины Арана Фауддви, измерения расстояния могут быть психологически и физиологически неверными. |
Мили Арана Фауддви: альбомная, портретная, печать и складывание PDF The Miles of Aran Fawddwy ’следует за 7.Маршрут в виде уродливого параллелограмма длиной 2 мили от долины Сим Сайварч недалеко от Динас Моуддви, вверх на северо-запад под хребет Глазгвм, на северо-восток до вершины, на юго-восток вдоль хребта Друс Бах, под вершиной Друсгула. и на юго-запад вниз по долине Хенгвм обратно к исходной точке. Направления важны для альтернативных макетов стихотворения: портретная версия представляет сам подъем, а альбомная версия представляет собой уплощенную версию параллелограммного гребня, описанного выше. Рис. 1: Версия для печати и складывания Фиг.2: Strava изображение маршрута |
Использование шрифтов, чтение и сцены, изображенные в пейзажах текста Шрифты, выбранные для стихотворения, включают Palatino для основного текста, мой основной концептуальный дорожный шрифт и Lucida Fax для слова «Miles». Lucida Fax выделен полужирным курсивом через 36 пунктов, имеет обрезной квадрат с засечками. Альбомная и портретная версии идентичны, за исключением положения заголовка, но следует отметить, что это расположение также является отличительной частью эстетической ценности стихотворения.В пейзажной версии название представляет собой реку Афон Ир Хенгвм, которая течет с северо-востока на юго-восток по дну долины Хенгвм и впадает в реку Дифи в Тан-и-Фоэль, недалеко от Динас Мауддви. Исток реки Дифи находится над озером Крейглин Дифи, прямо под вершиной горы, которая также упоминается в строке «Источник Дифи и источник предательства». Эта линия является ключевой для темы стихотворения, поскольку она представляет момент осознания в с трудом выигранных миль восхождения на вершину, что мы фактически не достигли вершины из-за плотного облачного покрова.Только при спуске были видны две вершины на плато на вершине горы, главная вершина все еще стояла решительно, теперь почти насмешливо, над озером и истоком реки Дифи. В портретной версии URL-адрес включает именованный якорь, который всегда будет загружать текст внизу страницы, пока страница доступна для внутреннего доступа к веб-сайту. Если URL-адрес вводится независимо, без хэштега / имени привязки (#footofthehill), страница будет открываться, как и ожидалось, сверху.Это служит для автоматического сосредоточения внимания читателя на заголовке внизу страницы и первой строке «На восходящей миле противоречивых аппетитов ». Последовательность чтения последовательно идет вверх по странице после подъема. Название представляет собой автостоянку у основания подъема и последний табличный знак в конце нашего собственного крутого маршрута подъема и пологого спуска (или начало пологого подъема и более крутого спуска). По сути, портретная версия представляет собой изображение самого подъема, читаемого снизу вверх по странице, снова начиная со слова «восходящий», но теперь с весом миль, которые нужно преодолеть, давящими на пешехода. |
Стих 1: На подъеме мили противоречивых аппетитов : RGB 199, 154, 113 Цвет был взят из желтой стрелки на скале, показывающей маршрут следа, ведущего к гребню.Напоминанием о реалиях природы были разбросанные перья мертвого голубя, скорее всего, съеденного лисой. |
Стих 2: На задержке дыхания Миля восполнения отмелей : RGB 79, 28, 28 Цвет был взят из снимков болотного растения, напоминающего тайский овощ pak bung (болотная капуста). На вершине хребта ландшафт довольно ровный, вдоль заборов уложены доски, чтобы пешеходы не проваливались в мелководные болота и торф. |
Стих 3: О дезориентации мили невидимых вершин : RGB 124, 71, 39 Цвет был взят из вертикального камня, возведенного на холме из камней на вершине Арана Фауддви, среди сильных ветров и густых облаков. Он напоминает каменный палец, остальные пальцы которого зажаты в более широкой части основания скалы. Он указывает на небо, но единственное голубое небо под нами. |
Стих 4: О реализации мили ложных достижений : RGB 92, 115, 109 Цвет был взят со скалистого откоса, который простирается почти отвесным перепадом от настоящей вершины, на несколько сотен метров дальше по трассе.Дальнейший подъем вершины незначителен, но ощущение предательства облаков в ясный ясный день усиливается тем фактом, что я уже придумал ироническое название мили для «мили ложных достижений». |
Стих 5: По ногам Mile of Boggy Traversals : RGB 112, 115, 120 Цвет был взят с хребта Пен-Майн, горы с плоской вершиной, невидимой на маршруте подъема, но очень яркой с противоположной стороны долины Хенгвм.В этот момент земля очень мягкая и влажная и плохо поддерживает ноющие ноги. У подножия долины, недалеко от места, где река Афон Ир Хенгвм вытекает с холмов, большой компас был выложен на земле из белых камней, и он хорошо виден с вершины долины. |
Стих 6: На самых ярких милях сланцевых отражений : RGB 120, 116, 69 Цвет взят из черепа мертвой овцы.Пейзаж был покрыт рыхлым сланцем всех форм, покрытых узорами и цветами, которые мерцают на открытом солнце, но при внимательном рассмотрении кажется, что они больше не отображают узоры асемического языка, первоначально воспринимаемые на первый взгляд. |
Стих 7: На удивительной миле изобретательной резки : RGB 160, 65, 59 Цвет был взят из электрического кабеля, соединяющего ножницы для стрижки овец с автомобильным аккумулятором, который висел под капотом пикапа, преграждающего путь в конце пути.На ферме шла стрижка, и это была короткая передышка от реальных пейзажных тем, хотя за последние несколько миль были видны пучки шерсти. |
Стих 8: На сокращенном значении Mile of Fractal Departure : RGB 105, 100, 42 Цвет был взят из мха, растущего на сланцевом указателе направления для Арана Бенллина и Арана Фоуддви в конце дорожки. Знак отмечает начало более легкого маршрута к вершине этих двух гор, но в данном случае он отмечает только конец более сложного подъема и более легкого спуска. |
РЕШЕНИЕ: Найдите A B в параллелограмме, показанном на рис.
.Стенограмма видео
Хорошо, ребята старше 45 или даже параллелограмма и попросили вас найти внутри B, поэтому я собираюсь ставить X на подписи каждый раз, поскольку это то, что мы ищем.Как видите, я как бы уже выделил синим треугольник, на котором мы собираемся сосредоточиться. И я также напомню вам, поскольку это параллелограмм, если мы знаем, что сторона B D равна 10, мы также знаем сторону A D c B a. C равно 10. Итак, что за дерьмо, и просто сосредоточьтесь на этом синем треугольнике. Так что, если я собираюсь продавать ради извинения за любовные знаки, мне нужно знать его противоположный угол, то есть угол. Видите ли, я этого не знаю, но если бы я мог найти угол B, тогда я бы знал угол c и, следовательно, мог бы сначала найти X, нам нужно будет найти угол B. Фактически, это единственное, что мы можем найти с помощью знаков закона прямо сейчас. Так что установите этот знак 1 30 на 12 равно. Подпишите B больше 10. Теперь, когда вы пересечете умножение, вы получите 12 раз, что знак B будет в 10 раз больше знака 1 30. После того, как вы разделите на 12, а затем подпишетесь в стихе, мы можем записать этот угол . Знак B будет равен знаку в стихе 10, а не 12. Знак 1 30 Итак, снова убедитесь, что ваш калькулятор не работает в режиме градусов. Если вы напечатали его неправильно, вы должны найти этот угол. B равно 39,7. Итак, теперь, когда я знаю, что угол B равен 39.7 уже знал, что Anglais равняется 1 30 Таким образом, если вычесть оба значения из 1 80 И это даст вам понять, что другой угол равен 10,3 градуса. И теперь, когда я знаю угол. Видите ли, теперь я могу использовать знаки закона, чтобы найти сторону X или бывшего, представляющего сторону. Может быть, так. Я просто перетащу нас на другой экран. Мы собираемся установить наши законы размера, так что это будет знаком.
Фактически, это единственное, что мы можем найти с помощью знаков закона прямо сейчас. Так что установите этот знак 1 30 на 12 равно. Подпишите B больше 10. Теперь, когда вы пересечете умножение, вы получите 12 раз, что знак B будет в 10 раз больше знака 1 30. После того, как вы разделите на 12, а затем подпишетесь в стихе, мы можем записать этот угол . Знак B будет равен знаку в стихе 10, а не 12. Знак 1 30 Итак, снова убедитесь, что ваш калькулятор не работает в режиме градусов. Если вы напечатали его неправильно, вы должны найти этот угол. B равно 39,7. Итак, теперь, когда я знаю, что угол B равен 39.7 уже знал, что Anglais равняется 1 30 Таким образом, если вычесть оба значения из 1 80 И это даст вам понять, что другой угол равен 10,3 градуса. И теперь, когда я знаю угол. Видите ли, теперь я могу использовать знаки закона, чтобы найти сторону X или бывшего, представляющего сторону. Может быть, так. Я просто перетащу нас на другой экран. Мы собираемся установить наши законы размера, так что это будет знаком.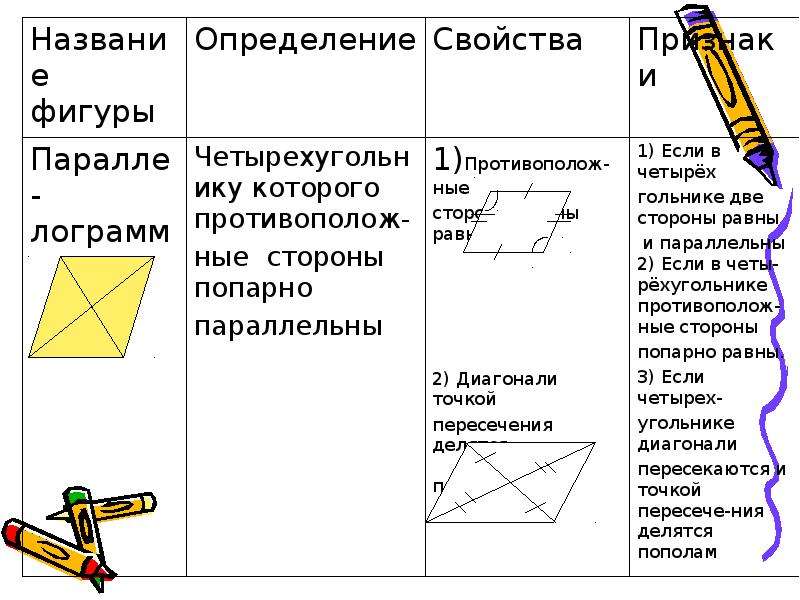 1 30 больше 12. Знак равенства 10.3 превышает эффекты. Так что крест умножьте. Получите время X. Подпишите 1 30 солений 12 раз. Знак 10.3. Вы хотите получить экс-вице. Также разделите мой знак 1 30 Теперь, когда я только сам, вы берете свой калькулятор Введите это так же, как вы видите его 12 раз со знаком 10.3. Разделите на Саймона, 30 лет. И вы должны получить этот X, который снова представляет сторону A B, которую мы хотели 2,8.
1 30 больше 12. Знак равенства 10.3 превышает эффекты. Так что крест умножьте. Получите время X. Подпишите 1 30 солений 12 раз. Знак 10.3. Вы хотите получить экс-вице. Также разделите мой знак 1 30 Теперь, когда я только сам, вы берете свой калькулятор Введите это так же, как вы видите его 12 раз со знаком 10.3. Разделите на Саймона, 30 лет. И вы должны получить этот X, который снова представляет сторону A B, которую мы хотели 2,8.
Полигонов — geom_polygon • ggplot2
Полигоны очень похожи на пути (как показано с помощью функции geom_path () )
за исключением того, что начальная и конечная точки соединены, а внутренняя часть
Цвет заливка . Группа эстетика определяет, какие корпуса
соединены в многоугольник. Начиная с R 3.6 и более поздних версий возможно
рисовать многоугольники с отверстиями, предоставляя эстетику подгруппы, которая
отличает точки внешнего кольца от тех, которые описывают отверстия в
многоугольник.
geom_polygon ( отображение = NULL, данные = NULL, stat = "личность", position = "личность", rule = "evenodd", ..., na.rm = ЛОЖЬ, show.legend = NA, inherit.aes = ИСТИНА )
Аргументы
| отображение | Набор эстетических карт, созданных с помощью |
|---|---|
| данные | Данные, которые будут отображаться в этом слое. Есть три варианты: Если Функция |
| стат | Статистическое преобразование данных, используемое для этого слой, как нить. |
| позиция | Регулировка положения, либо строка, либо результат вызов функции настройки положения. |
| правило | Либо |
| … | Другие аргументы передаются в |
| нарм | Если |
| показать. Легенда | логический. Стоит ли включать этот слой в легенды? |
| наследство aes | Если |
Эстетика
geom_polygon () понимает следующую эстетику (требуемая эстетика выделена жирным шрифтом):
xyальфацветзаполнениегруппаТип линииразмерподгруппа
Подробнее об установке эстетики в виньетке ("ggplot2-specs") .
См. Также
Примеры
# При использовании geom_polygon вам обычно нужны два фрейма данных:
# один содержит координаты каждого многоугольника (позиции), а
# другие значения, связанные с каждым многоугольником (значения). Идентификатор
# переменная связывает их вместе
ids <- factor (c ("1.1", "2.1", "1.2", "2.2", "1.3", "2.3"))
значения <- data.frame (
id = идентификаторы,
значение = c (3, 3.1, 3.1, 3.2, 3.15, 3.5)
)
позиции <- data.frame (
id = rep (идентификаторы, каждый = 4),
х = с (2, 1, 1.1, 2.2, 1, 0, 0.3, 1.1, 2.2, 1.1, 1.2, 2.5, 1.1, 0.3,
0,5, 1,2, 2,5, 1,2, 1,3, 2,7, 1,2, 0,5, 0,6, 1,3),
у = с (-0,5, 0, 1, 0,5, 0, 0,5, 1,5, 1, 0,5, 1, 2,1, 1,7, 1, 1,5,
2.2, 2.1, 1.7, 2.1, 3.2, 2.8, 2.1, 2.2, 3.3, 3.2)
)
# В настоящее время нам нужно вручную объединить два вместе
datapoly <- merge (значения, позиции, by = c ("id"))
p <- ggplot (datapoly, aes (x = x, y = y)) +
geom_polygon (aes (fill = значение, group = id))
п
# Кажется, много работы, но потом легко добавить
# другие функции в этой системе координат, например. грамм.:
поток <- data.frame (
x = cumsum (runif (50, max = 0,1)),
y = cumsum (runif (50, max = 0,1))
)
p + geom_line (data = stream, color = "grey30", size = 5)
# И если позиции указаны по долготе и широте, вы можете использовать
# corre_map для создания различных картографических проекций.
if (packageVersion ("grid")> = "3.6") {
# Начиная с версии R 3.6 geom_polygon () поддерживает многоугольники с отверстиями
# Используйте эстетику подгруппы, чтобы отличить отверстия от основного многоугольника
дыры <- do.call (rbind, lapply (split (datapoly, datapoly $ id), function (df) {
df $ x <- df $ x + 0.5 * (среднее (df $ x) - df $ x)
df $ y <- df $ y + 0,5 * (среднее (df $ y) - df $ y)
df
}))
datapoly $ subid <- 1L
отверстия $ subid <- 2L
datapoly <- rbind (данные, дыры)
p <- ggplot (datapoly, aes (x = x, y = y)) +
geom_polygon (aes (fill = значение, group = id, subgroup = subid))
п
}
грамм.:
поток <- data.frame (
x = cumsum (runif (50, max = 0,1)),
y = cumsum (runif (50, max = 0,1))
)
p + geom_line (data = stream, color = "grey30", size = 5)
# И если позиции указаны по долготе и широте, вы можете использовать
# corre_map для создания различных картографических проекций.
if (packageVersion ("grid")> = "3.6") {
# Начиная с версии R 3.6 geom_polygon () поддерживает многоугольники с отверстиями
# Используйте эстетику подгруппы, чтобы отличить отверстия от основного многоугольника
дыры <- do.call (rbind, lapply (split (datapoly, datapoly $ id), function (df) {
df $ x <- df $ x + 0.5 * (среднее (df $ x) - df $ x)
df $ y <- df $ y + 0,5 * (среднее (df $ y) - df $ y)
df
}))
datapoly $ subid <- 1L
отверстия $ subid <- 2L
datapoly <- rbind (данные, дыры)
p <- ggplot (datapoly, aes (x = x, y = y)) +
geom_polygon (aes (fill = значение, group = id, subgroup = subid))
п
} Схема моделирования для параллелограмма и повернутого квадрата DLD .
 ..
..Контекст 1
... демонстрирует уменьшение эффективного наклона, мы смоделировали среднюю часть двух DLD-устройств (рис.6), один в виде параллелограмма (фиг. 6B), а другой в виде повернутого квадрата (фиг. 6C). Каждое устройство имеет 152 круглых столба вдоль потока и 120 столбов в поперечном направлении. Диаметр штифта составляет 10 мкм, а зазор между штырями - 10 мкм. Смоделированная область 3,2 мм × 2,4 мм (3200 × 2400 ячеек решетки) с ...
Контекст 2
... демонстрирует уменьшение эффективного наклона, мы смоделировали среднюю часть двух DLD-устройств ( Инжир.6), один в виде параллелограмма (фиг. 6B), а другой в виде повернутого квадрата (фиг. 6C). Каждое устройство имеет 152 круглых столба вдоль потока и 120 столбов в поперечном направлении. Диаметр штифта составляет 10 мкм, а зазор между штырями - 10 мкм. Смоделированная область имеет размер 3,2 мм × 2,4 мм (3200 × 2400 ячеек решетки) с периодическими условиями потока на входе и выходе . ..
..
Контекст 3
... продемонстрировать уменьшение эффективного наклона, мы смоделировали среднюю разрез двух устройств DLD (рис.6), один в виде параллелограмма (фиг. 6B), а другой в виде повернутого квадрата (фиг. 6C). Каждое устройство имеет 152 круглых столба вдоль потока и 120 столбов в поперечном направлении. Диаметр штифта составляет 10 мкм, а зазор между штырями - 10 мкм. Смоделированная область составляет 3,2 мм × 2,4 мм (3200 × 2400 ячеек решетки) с периодическими условиями потока на входе и выходе (рис. 6A). Поток управляется градиентом давления ...
Контекст 4
... (Рис.6B), а другой - в виде повернутого квадрата (фиг. 6C). Каждое устройство имеет 152 круглых столба вдоль потока и 120 столбов в поперечном направлении. Диаметр штифта составляет 10 мкм, а зазор между штырями - 10 мкм. Смоделированная область составляет 3,2 мм × 2,4 мм (3200 × 2400 ячеек решетки) с периодическими условиями потока на входе и выходе (рис. 6A). Поток приводится в движение градиентом давления в осевом направлении. Каждое устройство имеет две секции массива с противоположными наклонами. Левая часть имеет положительный наклон решетки ε = 0.2, а правое сечение имеет наклон ε = −0,2. Обе секции разделены промежутком ≈4 столбика (80 ...
6A). Поток приводится в движение градиентом давления в осевом направлении. Каждое устройство имеет две секции массива с противоположными наклонами. Левая часть имеет положительный наклон решетки ε = 0.2, а правое сечение имеет наклон ε = −0,2. Обе секции разделены промежутком ≈4 столбика (80 ...
Контекст 5
... линии тока (синие линии) показаны (рис. 6B и C) для обоих устройств. В устройстве параллелограмма ( На рис. 6В) линия тока, ближайшая к правой боковой стенке, остается горизонтальной повсюду.По мере удаления от правой боковой стенки к центральной линии устройства линии тока начинают наклоняться вдоль преобладающего наклона решетки.Уже десять столбов от правой стороны ...
Контекст 6
... линии тока (синие линии) показаны (рис. 6B и C) для обоих устройств. В устройстве параллелограмма (фиг. 6B) линия тока, ближайшая к правой боковой стенке, остается горизонтальной на всем протяжении. По мере того, как они перемещаются от правой боковой стенки к центральной линии устройства, линии тока начинают наклоняться в соответствии с преобладающим наклоном решетки. Уже через десять столбов от правой стены этот эффект становится важным, и наклон продолжает расти...
Уже через десять столбов от правой стены этот эффект становится важным, и наклон продолжает расти...
Контекст 7
... устройство повернутого квадрата (рис. 6C), линии тока (синие линии) горизонтальны. Линии тока остаются на прогнозируемом курсе (горизонтальный «зигзаг» вокруг стоек) параллельно боковым стенкам устройства. Это можно объяснить отсутствием анизотропии. В отличие от схемы параллелограмма, использование массива повернутых квадратов приводит к четко определенному и постоянному ...
Context 8
... исследованию поля потока в устройстве параллелограмма (рис.6B), мы обнаруживаем, что анизотропный боковой перепад давления начинает высвобождаться вблизи границы раздела секции решетки, что проявляется как вторичная рециркуляция в устройстве. Мы изобразим эту сложную «лестничную» схему рециркуляции фонового потока на рис. ...
Контекст 9
... устройство, имитирующее эксперимент с треугольными столбами 160 × 120 вдоль потока и поперечного направления, соответственно.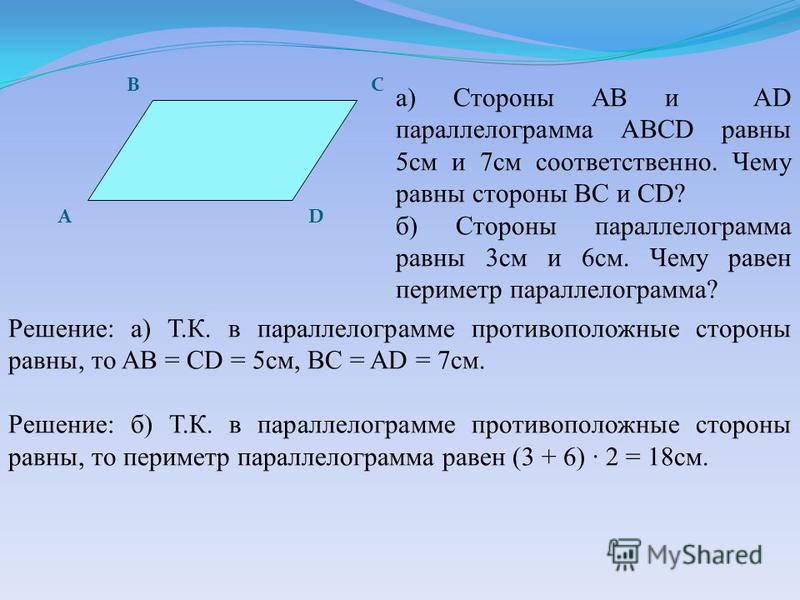 Наклон составляет ε = −0,1, а параметры устройства соответствуют параметрам эксперимента (размер штифта 6 мкм, зазор 4 мкм).Граничные условия для смоделированного устройства (3200 × 2400 ячеек решетки) такие же, как на фиг. 6A. Область моделирования состоит из двух секций арматуры, при этом треугольные стойки в правой секции повернуты на 90 ° по сравнению со стойками в левой секции. Центральный межфазный зазор составляет ≈50 мкм и моделируется без цилиндрических опор крыши. Рис. 10D показывает подмножество области моделирования на правой боковой стене с потоком ...
Наклон составляет ε = −0,1, а параметры устройства соответствуют параметрам эксперимента (размер штифта 6 мкм, зазор 4 мкм).Граничные условия для смоделированного устройства (3200 × 2400 ячеек решетки) такие же, как на фиг. 6A. Область моделирования состоит из двух секций арматуры, при этом треугольные стойки в правой секции повернуты на 90 ° по сравнению со стойками в левой секции. Центральный межфазный зазор составляет ≈50 мкм и моделируется без цилиндрических опор крыши. Рис. 10D показывает подмножество области моделирования на правой боковой стене с потоком ...
Самый ужасающий стих в Библии
Ключевой ингредиент настоящего лагосианца - это способность «изменить это» для человека.Это значит: критиковать человека, часто после неуместной провокации. Это потому, что Лагос, Центр Stresselence (стресса и совершенства), полон тестировщиков терпения, высокомерных разочарователей и намеренно тупых людей. Если у терпеливой собаки самая толстая кость, это только потому, что лагозианская собака съела все мясо!
Пора "изменить это" по-настоящему?
Именно на этом фоне Бог призывает меня, истинную лагозианку, иметь мягкий и тихий дух. Когда я впервые прочитал 1 Петра 3: 4, меня охватил ужас.Не только потому, что я больше не мог «это изменить», но и потому, что за все мои годы меня никогда не называли мягким или тихим.
Когда я впервые прочитал 1 Петра 3: 4, меня охватил ужас.Не только потому, что я больше не мог «это изменить», но и потому, что за все мои годы меня никогда не называли мягким или тихим.
За все годы меня никогда не называли ласковым или тихим
Моя жизнерадостная экстравертная личность была чем-то, чем я очень гордился. На самом деле мне нравилось, что я мог осветить комнату, просто войдя в нее, и что людям это нравилось во мне. Поэтому я не стал прятать свой блеск под бушелем. Однако казалось, что этот стих просил меня сделать именно это.Это заставило меня столкнуться с проблемой, о которой я даже не подозревал, что слишком долго бродил по дороге: библейской женственностью.
Кроткий и тихий дух - нет! Картина «библейской женщины», которую нам часто представляют, - это женщина, которая застенчива и покорна. Такие стихи, как 1 Петра 3: 4, похоже, способствуют созданию этого непривлекательного образа. Мы можем обойти проблему и сказать, что этот текст адресован только женам или женщинам в определенном древнем контексте, или мы можем засучить рукава и противостоять тексту. Мы часто виновны в том, что читаем Библию, исходя из собственных предположений. Таким образом, этот текст наполнил меня тревогой, потому что я видел, что мягкость и тишина означают бездействие, робость и подавленность. Но это не так.
Мы часто виновны в том, что читаем Библию, исходя из собственных предположений. Таким образом, этот текст наполнил меня тревогой, потому что я видел, что мягкость и тишина означают бездействие, робость и подавленность. Но это не так.
Я видел в кротости и покое состояние покоя, робости и подавленности. Но это не
Кротость можно перевести как кротость, которую не следует принимать за слабость. Кротость - это способность контролировать свою силу или ограничивать ее, а не ее отсутствие.Это значит быть обучаемым, милосердным и скромным. Его можно определить как качество доброты и внимательности. Мне напоминают, что кротость - это плод Духа (Галатам 5: 22–23). Это означает, что по мере того, как мы соответствуем образу Христа, мы начнем показывать доказательства того, что Его Дух обитает в нас, что для женщин, согласно 1 Петра 3: 4, включает в себя кроткий и тихий дух.
Божий замысел: библейская женственность «Библейская женственность» - это не искусство быть робким и подавленным.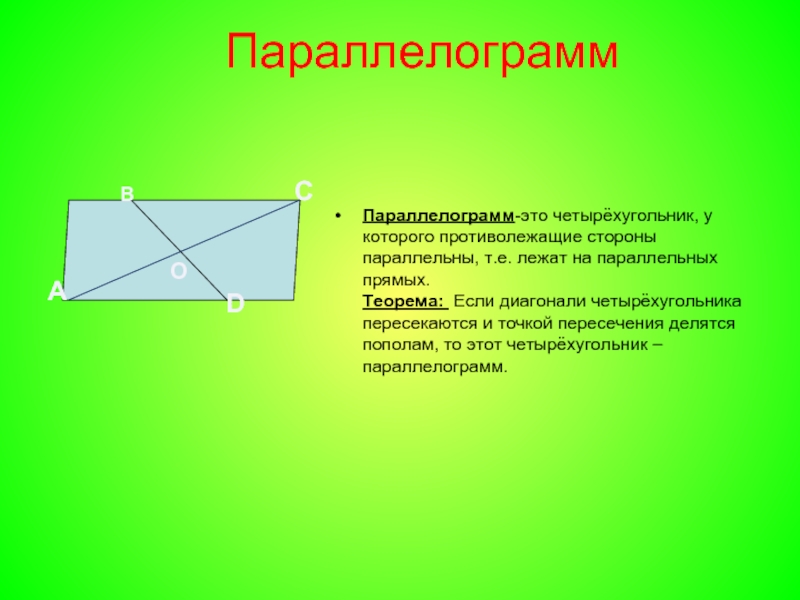 Это просто Божий замысел для женщин, и это хорошо. Это для всех женщин, в любое время года, всех возрастов, из всех слоев общества, всех типов личности. Важно отметить, что это подтверждает, что мы не запоздалые мысли. Мы imago dei - созданы по образу и подобию Бога. Таким образом, женщины отличаются от мужчин, но при этом равны в достоинстве и значении (Бытие 1:27).
Это просто Божий замысел для женщин, и это хорошо. Это для всех женщин, в любое время года, всех возрастов, из всех слоев общества, всех типов личности. Важно отметить, что это подтверждает, что мы не запоздалые мысли. Мы imago dei - созданы по образу и подобию Бога. Таким образом, женщины отличаются от мужчин, но при этом равны в достоинстве и значении (Бытие 1:27).
Женщины отличаются от мужчин, но равны по достоинству и достоинству (Бытие 1:27)
Библия прославляет разнообразие
Если и есть что-то христианство, так это преобразование.Ибо все мы становимся новыми творениями во Христе, рожденными в новую жизнь, чтобы сообразиться образу Христа (Римлянам 12: 2; 2 Коринфянам 5:17; Римлянам 8:29). Соответствие Христу не лишает нас нашего разнообразия. Библия признает наши различия в способностях, личности и этнической принадлежности. Он утверждает, что Бог создал все, действует во всем и все использует для Своей славы.
Павел прославляет разнообразие: «Дары разные, но Дух один и тот же; и есть разновидности служения, но один и тот же Господь; и есть разные действия, но один и тот же Бог дает им силу в каждом »(1 Коринфянам 12: 4–6). Апостол Иоанн пишет: «После сего я взглянул и вот, великое множество людей, которых никто не мог сосчитать, из каждого народа, из всех колен, народов и языков, стоящих перед престолом и перед Агнцем, в белых одеждах, с пальмовые ветви в своих руках и громкий возглас: «Спасение принадлежит Богу нашему, сидящему на престоле, и Агнцу» (Откровение 7: 9).
Апостол Иоанн пишет: «После сего я взглянул и вот, великое множество людей, которых никто не мог сосчитать, из каждого народа, из всех колен, народов и языков, стоящих перед престолом и перед Агнцем, в белых одеждах, с пальмовые ветви в своих руках и громкий возглас: «Спасение принадлежит Богу нашему, сидящему на престоле, и Агнцу» (Откровение 7: 9).
Благочестивая женщина - во всех ее обличьях
В Библии благочестивая женщина выражается по-разному:
- Книга Судей 4 представляет Девору как лидера, благочестивого пророка и судью над Израилем
- Книга Руфи рассказывает нам историю женщины, которая проявляет бескорыстное сострадание
- Притчи 31 иллюстрируют замечательную богобоязненную жену и деловую женщину
- Книга Деяний представляет Доркас, ученицу, который был полон добрых дел и дел милосердия (Деяния 9:36).
- Деяния 16: 14–16 объявляет о Лидии, продавщице пурпурных товаров и поклоняющейся Богу, которая помогала Павлу в благополучии
- Деяния 18: 24–26 показывает Присциллу вместе со своим мужем Акилой, обучающими Аполлоса.
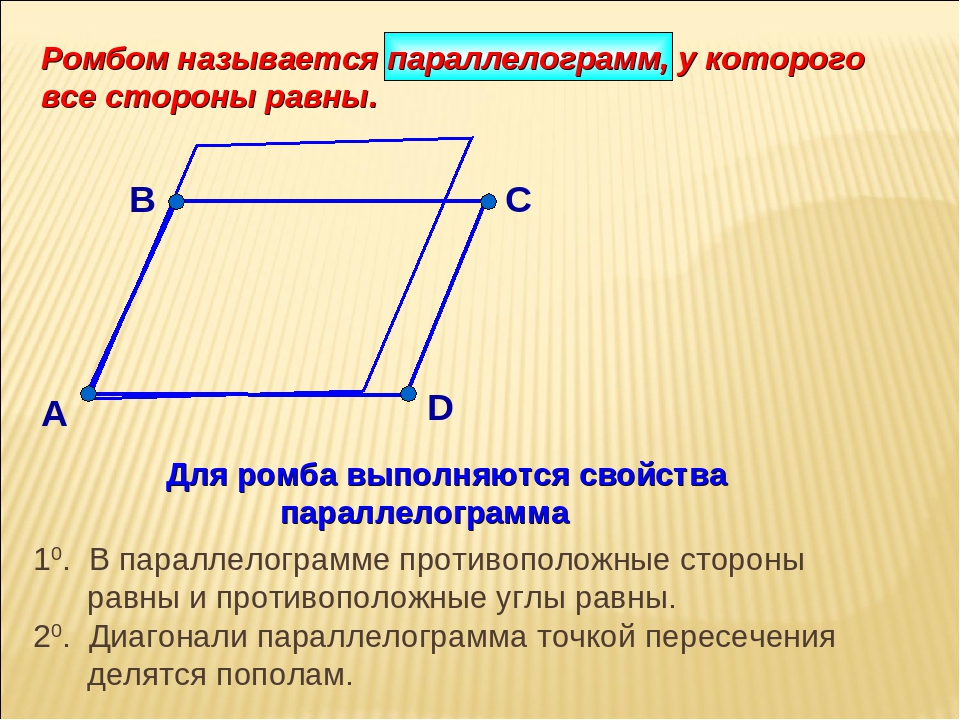
- В Послании к Римлянам 16: 1-2 упоминается Фиби, служительница церкви Кенхриан
- Колоссянам 4:15 цитируется Нимфа, которая содержала домашнюю церковь
- Титу 2: 3-5 показывает мать, жену и домохозяйку, которые наставляют молодых женщин и жен.
Эти женщины представляют широкий спектр личностных качеств, способностей и слоев общества. Тем не менее, Священное Писание считает каждую женщину хорошим примером благочестивой женственности. Поэтому рассмотрим эту несколько вызывающую аналогию с библейской женственностью.
Соответствие Христу не лишает нас нашего разнообразия.
Если бы вам сказали, что необходимо заполнить четырехстороннее (или четырехстороннее) отверстие, на ум сразу же пришел бы квадрат, который подойдет. Но то же самое было бы с прямоугольником, ромбом, параллелограммом, трапецией или воздушным змеем.Хотя у них есть уникальные атрибуты, которые делают их разными, их объединяют основные свойства многоугольника. Несмотря на то, что, как и большинство аналогий, ошибочны, это служит полезной картиной библейской женственности, которую можно показать бесчисленным множеством способов и которая все же будет поучительной во всех ее формах.
Несмотря на то, что, как и большинство аналогий, ошибочны, это служит полезной картиной библейской женственности, которую можно показать бесчисленным множеством способов и которая все же будет поучительной во всех ее формах.
Библейская женственность должна быть надежной в применении. Ибо Бог сотворил замечательный круг разных женщин. Наше единство во Христе означает, что мы можем воплощать в жизнь Его замысел независимо от нашей культуры, возраста, семейного или социально-экономического положения.Цель библейской женственности - прославлять Бога везде, где мы находимся.
1 Петра 3: 4 не должно обескураживать тех из нас, кто более игрив и экстравертирован. Он не учит однообразному соответствию. Скорее, он описывает атрибут, который должен принадлежать разным женщинам во Христе. В центре внимания этого текста - наши сердца - быть милосердными и обучаемыми, слушать, прежде чем говорить, и оставаться смиренными.
Смирение - это не черта личности; ни один из них не поддается обучению или благотворительности.

 Говорят, что «мили Ринога» — это коварные вещи, полные влажных, весенних болот, острых камней, скрытых под кустами, папоротника и хохолка, и внезапно дезориентирующего облачного покрова, который затрудняет навигацию с помощью компаса. Прогуливаясь по хребту от Глазгвм, легко поддаться насмешкам обманом миль Ринога, только здесь они задуманы как «Аранские мили».
Говорят, что «мили Ринога» — это коварные вещи, полные влажных, весенних болот, острых камней, скрытых под кустами, папоротника и хохолка, и внезапно дезориентирующего облачного покрова, который затрудняет навигацию с помощью компаса. Прогуливаясь по хребту от Глазгвм, легко поддаться насмешкам обманом миль Ринога, только здесь они задуманы как «Аранские мили». Пейзажную поэму в распечатанном виде можно сложить трижды между стихами 2 и 3, 4 и 5, 6 и 7, а затем поставить на горизонтальное основание так, чтобы текст был обращен внутрь в ромбовидном узоре (см. Рис. 1 ниже). Если его расположить в форме замкнутого ромба с левым и правым краями, направленными на юг, он образует грубую трехмерную модель параллелограммного маршрута вдоль гребня (см. Рис. 2 ниже).
Пейзажную поэму в распечатанном виде можно сложить трижды между стихами 2 и 3, 4 и 5, 6 и 7, а затем поставить на горизонтальное основание так, чтобы текст был обращен внутрь в ромбовидном узоре (см. Рис. 1 ниже). Если его расположить в форме замкнутого ромба с левым и правым краями, направленными на юг, он образует грубую трехмерную модель параллелограммного маршрута вдоль гребня (см. Рис. 2 ниже). В пейзажной версии стихотворения он представляет собой долгую тащу, наклоненную вперед под тяжестью крутых подъемов и больших расстояний.В нем есть трудолюбивая ступня, которая захватывает гребень маршрута между пешеходами и скалистые выступы на краю головокружительных откосов. Отвесные капли изображены горизонтальными вертикальными линиями, спускающимися от оснований «миль». Эти линии изображают овраги, ручьи и темные контуры, которые окружает пешеход на обратном пути вниз по долине Хенгвм. На вершине гребня первые строки каждого стиха представляют разные высоты вересковой пустоши, начиная со слова «восходящий» слева и заканчивая словом «сокращенно» справа.Сами названия миль пишутся с заглавной буквы и выделяются курсивом. Использование заглавных букв представляет собой формализацию названий собственных существительных, которые вызывают их собственную (сельскую) городскую легендарную ценность как воплощение идеи «аранских миль», чтобы иронично контрастировать с устоявшейся репутацией «миль риног».
В пейзажной версии стихотворения он представляет собой долгую тащу, наклоненную вперед под тяжестью крутых подъемов и больших расстояний.В нем есть трудолюбивая ступня, которая захватывает гребень маршрута между пешеходами и скалистые выступы на краю головокружительных откосов. Отвесные капли изображены горизонтальными вертикальными линиями, спускающимися от оснований «миль». Эти линии изображают овраги, ручьи и темные контуры, которые окружает пешеход на обратном пути вниз по долине Хенгвм. На вершине гребня первые строки каждого стиха представляют разные высоты вересковой пустоши, начиная со слова «восходящий» слева и заканчивая словом «сокращенно» справа.Сами названия миль пишутся с заглавной буквы и выделяются курсивом. Использование заглавных букв представляет собой формализацию названий собственных существительных, которые вызывают их собственную (сельскую) городскую легендарную ценность как воплощение идеи «аранских миль», чтобы иронично контрастировать с устоявшейся репутацией «миль риног».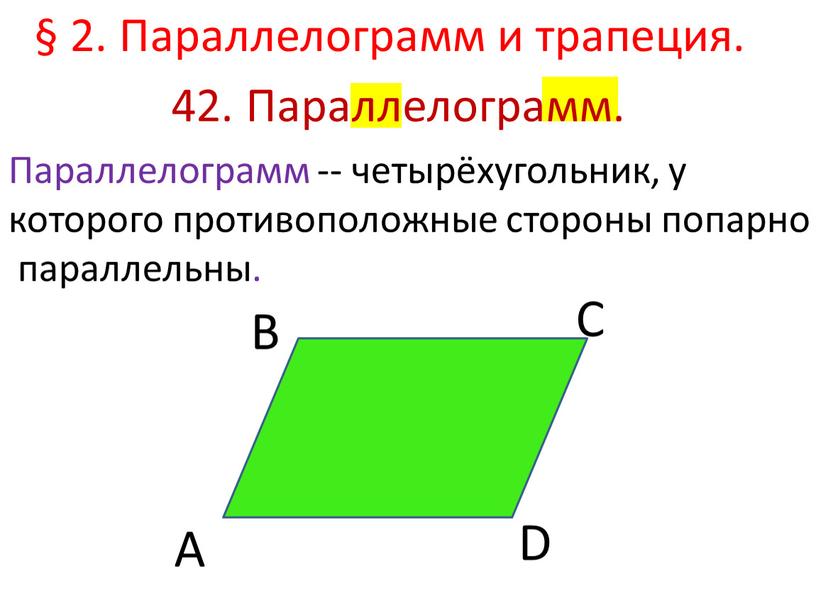 Курсив снова используется, чтобы показать напряженную деятельность, которую потребовалось, чтобы покрыть и осознать эти мили.
Курсив снова используется, чтобы показать напряженную деятельность, которую потребовалось, чтобы покрыть и осознать эти мили.
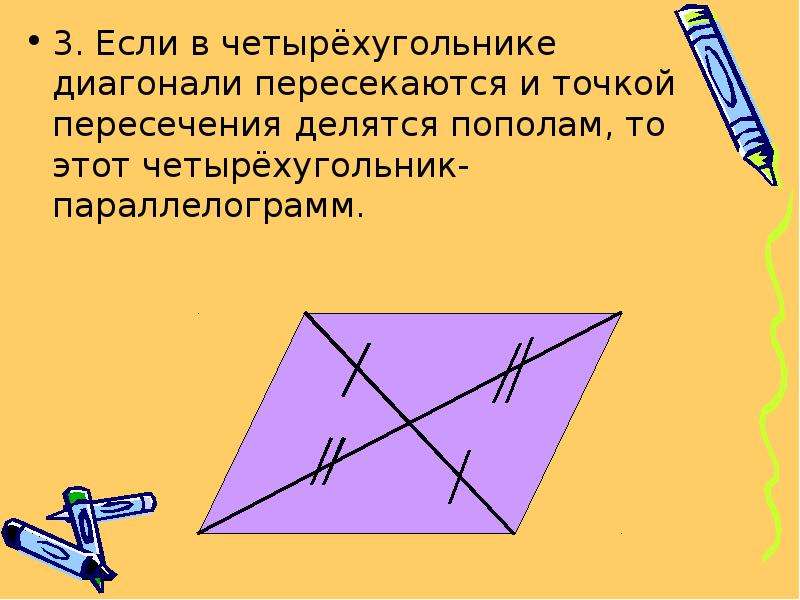 В каждом чтении ориентиры и происшествия на маршруте идентичны. Другая перспектива обеспечивается ориентацией страницы и положением заголовка. Цвета прорезей линий и названия миль курсивом были взяты из фотографий ландшафта с каждой из последовательных миль.
В каждом чтении ориентиры и происшествия на маршруте идентичны. Другая перспектива обеспечивается ориентацией страницы и положением заголовка. Цвета прорезей линий и названия миль курсивом были взяты из фотографий ландшафта с каждой из последовательных миль.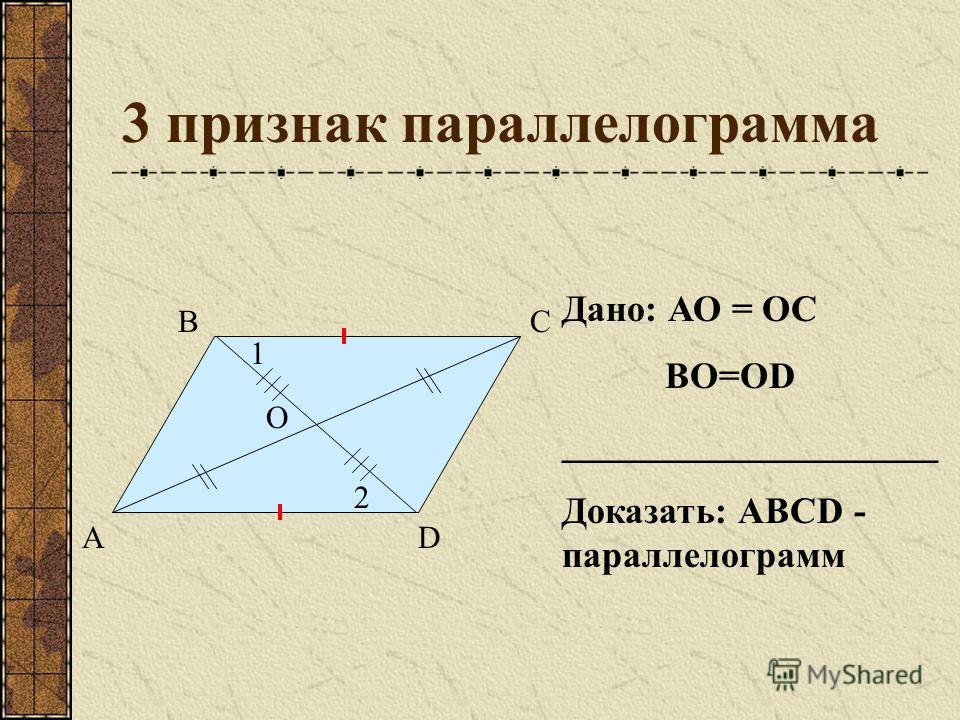
 Он был создан, чтобы отразить чувство достижения, которое вы испытываете при достижении вершины, только чтобы понять, что спуск вниз может быть еще более сложным.
Он был создан, чтобы отразить чувство достижения, которое вы испытываете при достижении вершины, только чтобы понять, что спуск вниз может быть еще более сложным.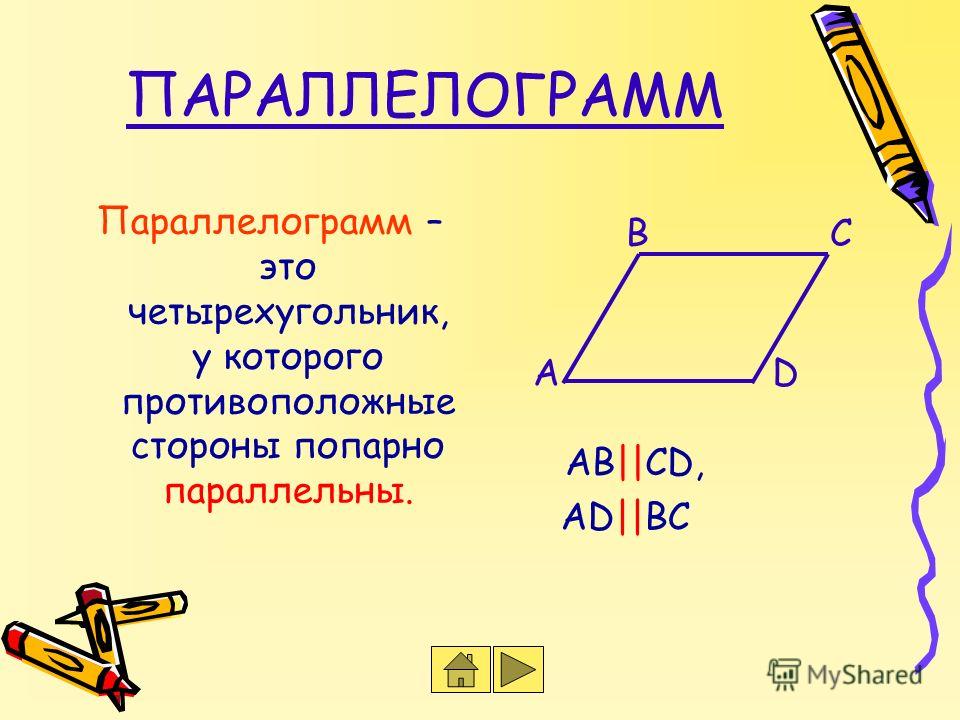 Холмы также усеяны останками нескольких ягнят, которые, похоже, были убиты лисами. Это также показано в предыдущем стихе со строкой «Приближаясь к голове барана Хенгвма».
Холмы также усеяны останками нескольких ягнят, которые, похоже, были убиты лисами. Это также показано в предыдущем стихе со строкой «Приближаясь к голове барана Хенгвма». Это обозначило конец маршрута на расстоянии 7,2 мили, отсюда и «сокращенная миля». Независимо от направления фрактальная геометрия маршрута теперь описывается в развивающемся тексте.
Это обозначило конец маршрута на расстоянии 7,2 мили, отсюда и «сокращенная миля». Независимо от направления фрактальная геометрия маршрута теперь описывается в развивающемся тексте. Все объекты будут укреплены для создания фрейма данных. Видеть
Все объекты будут укреплены для создания фрейма данных. Видеть  См. Примеры в
См. Примеры в 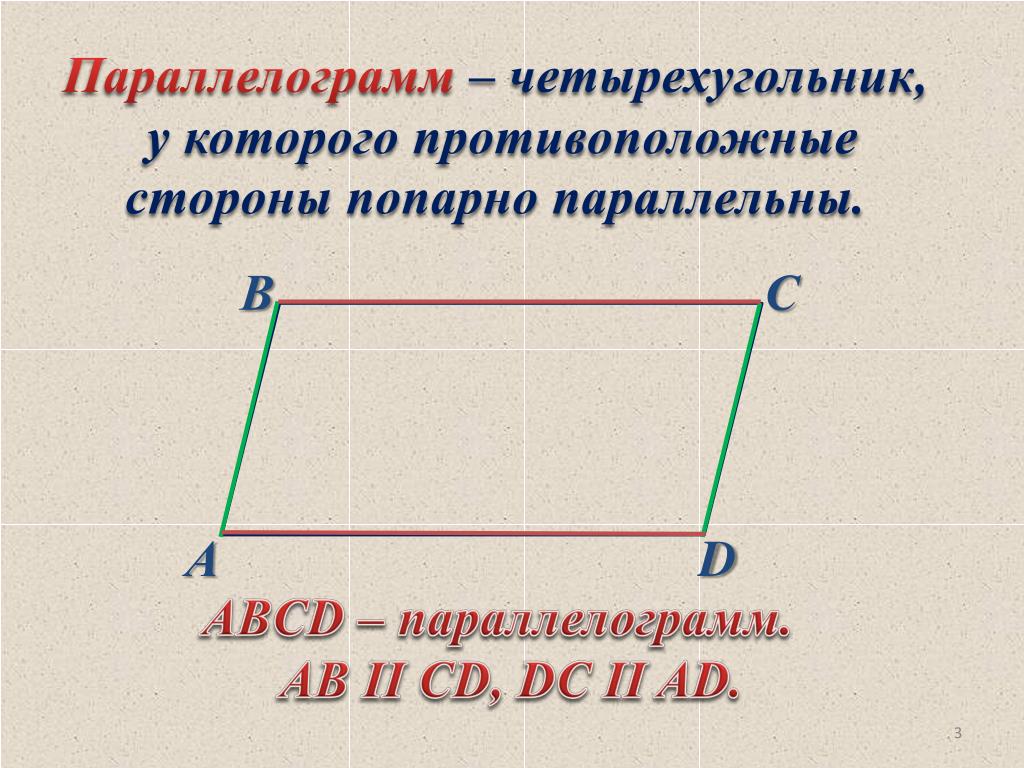
Leave a Reply