Найти сумму натуральных чисел от 1 до 100: найти сумму всех натуральных чисел от 1 до 100
Найти сумму чисел от 1 до 15. Занимательная математика: правило Гаусса
помогите пожалуйста!! вычислите сумму натуральных чисел от 1+2+3+4+…+97+98+99+100. и получил лучший ответ
Ответ от Александр Хейнонен[гуру]
Выдающегося немецкого математика Карла Фридриха Гаусса (1777-1855) современники называли «королём математики» .
Ещё в раннем детстве он проявлял незаурядные математические способности. В возрасте трех лет Гаусс уже исправлял счета отца.
Рассказывают, что в начальной школе, где учился Гаусс (6 лет) , учитель, чтобы занять класс на продолжительное время самостоятельной работой, дал задание ученикам — вычислить сумму всех натуральных чисел от 1 до 100. Маленький Гаусс ответил на вопрос почти мгновенно, чем невероятно удивил всех и, прежде всего, учителя.
Давайте попробуем устно решить задачу о нахождении суммы указанных выше чисел. Для начала возьмём сумму чисел от 1 до 10: 1 +2 + 3 + 4 + 5 + 6 + +7 + 8 + 9 + 10.
Гаусс обнаружил, что 1 + 10 = 11, и 2 + 9 = 11, и так далее.
Гаусс увидел, что сложение чисел всего ряда следует проводить попарно, и составил алгоритм быстрого сложения чисел от 1 до 100.
1 2 3 4 5 6 7 8 …49 50 51 52 …94 95 96 97 98 99 100
1. Необходимо подсчитать количество пар чисел в последовательности от 1 до 100. Получаем 50 пар.
2. Складываем первое и последнее числа всей последовательности. В нашем случае это 1 и 100. Получаем 101.
3. Умножаем количество пар чисел в последовательности на полученную в пункте 2 сумму. Получаем 5050.
Таким образом, сумма натуральных чисел от 1 до 100 равна 5050.
Простая формула: сумма чисел от 1 до n = n * (n+1) : 2. Вместо n подставляйте последнее число и вычисляйте.
Проверьте! Это работает!
Ответ от Ђаня Фертикова [новичек]
5050
Ответ от Михаил Медведев [активный]
5050
Ответ от Павел соломенников [новичек]
5050
Ответ от Алевтина башкова [новичек]
5050
Ответ от Ђигр Тихомирова [активный]
5050
Ответ от Мария дубровина [новичек]
5050
Ответ от Ѐавил Бадиров [новичек]
5050
Ответ от Дмитрий [активный]
5050
Ответ от Евгений Саяпов [активный]
5050
Ответ от 2 ответа [гуру]
Содержимое:
Целые числа – это числа, не содержащие дробную или десятичную часть. Если в задаче требуется сложить определенное количество целых чисел от 1 до заданного значения N, то их не нужно складывать вручную. Вместо этого воспользуйтесь формулой (N(N+1))/2, где N — наибольшее число ряда.
Если в задаче требуется сложить определенное количество целых чисел от 1 до заданного значения N, то их не нужно складывать вручную. Вместо этого воспользуйтесь формулой (N(N+1))/2, где N — наибольшее число ряда.
Шаги
- 1 Определите наибольшее целое число (N). Суммируя целые числа от 1 до любого заданного числа N, вы должны определить значение N (N не может быть десятичным числом или дробью или отрицательным числом).
- Пример. Найдите сумму всех целых чисел от 1 до 100. В этом случае N=100, так как это наибольшее (и конечное) число данного вам числового ряда.
- 2 Умножьте N на (N +1) и разделите результат умножения на 2. Когда вы определили целое значение N, подставьте его в формулу (N(N+1))/2 и вы найдете сумму всех целых чисел от 1 до N.
- Пример. Подставьте N=100 и получите (100(100+1))/2.
- 3 Запишите ответ. Окончательный ответ есть сумма всех целых чисел от 1 до данного N.
- Пример.
- (100(100+1))/2 =
- (100(101))/2 =
- (10100)/2 = 5050
- Сумма всех целых чисел от 1 до 100 равна 5050.

- Пример.
- 4 Вывод формулы (N(N+1))/2. Еще раз рассмотрим вышеописанный пример. Мысленно разделите ряд 1 + 2 + 3 + 4 + … + 99 + 100 на два ряда — первый от 1 до 50, а второй от 51 до 100. Если вы сложите первое число (1) первого ряда и последнее число (100) второго ряда, то вы получите 101. Вы также получите 101, если сложите 2 и 99, 3 и 98, 4 и 97, и так далее. Если каждое число первой группы сложить с соответствующим числом второй группы, то в итоге мы получим 50 чисел, каждое из которых равно 101. Поэтому 50*101 = 5050 — сумма чисел от 1 до 100. Обратите внимание, что 50 = 100/2 и 101 = 100 + 1. На самом деле это справедливо для суммы любых положительных целых чисел: их суммирование можно разбить на два этапа с двумя рядами чисел, причем соответствующие числа в каждом ряду могут быть сложены друг с другом, а результат сложения будет одинаковым.
- Можно сказать, что сумма целых чисел от 1 до N равна (N/2)(N+1). Упрощенная запись этой формулы есть формула (N(N+1))/2.

- Можно сказать, что сумма целых чисел от 1 до N равна (N/2)(N+1). Упрощенная запись этой формулы есть формула (N(N+1))/2.
Вычисление суммы чисел, расположенных между двумя числами, посредством суммы от 1 до N
- 1 Определите вариант суммирования (включительно или нет). Часто в задачах вместо того, чтобы найти сумму чисел от 1 до заданного числа N, просят найти сумму целых чисел от N 1 до N 2 , где N 2 > N 1 и оба числа > 1. Вычислить такую сумму довольно просто, но, прежде чем приступать к вычислениям, вы должны определить, включаются ли данные числа в N 1 и N 2 в конечную сумму или нет.
- 2
Чтобы найти сумму целых чисел между двумя числами N 1 and N 2 , отдельно найдите сумму до N 1 , отдельно найдите сумму до N 2 и вычтите их друг из друга (вычтите сумму до меньшего значения N из суммы до большего значения N).
При этом важно знать, суммировать ли включительно или нет. При суммировании включительно вы должны вычесть 1 из данного значения N 1 ; в противном случае вы должны вычесть 1 из данного значения N 2 .
- Пример. Найдем сумму («включительно») целых чисел от N 1 = 75 до N 2 = 100.
 Другими словами, мы должны найти 75 + 76 + 77 + … + 99 + 100. Чтобы решить задачу, мы должны найти сумму целых чисел от 1 до N 1 -1, а затем вычесть ее от суммы чисел от 1 до N 2 (запомните: при суммировании включительно мы вычитаем 1 из N 1):
Другими словами, мы должны найти 75 + 76 + 77 + … + 99 + 100. Чтобы решить задачу, мы должны найти сумму целых чисел от 1 до N 1 -1, а затем вычесть ее от суммы чисел от 1 до N 2 (запомните: при суммировании включительно мы вычитаем 1 из N 1):- (N 2 (N 2 + 1))/2 — ((N 1 -1)((N 1 -1) + 1))/2 =
- (100(100 + 1))/2 — (74(74 + 1))/2 =
- 5050 — (74(75))/2 =
- 5050 — 5550/2 =
- 5050 — 2775 = 2275. Сумма чисел от 75 до 100 («включительно») равна 2275.
- Теперь найдем сумму чисел без включения данных чисел (другими словами, мы должны найти 76 + 77 + … + 99). В этом случае мы вычитаем 1 из N 2:
- ((N 2 -1)((N 2 -1) + 1))/2 — (N 1 (N 1 + 1))/2 =
- (99(99 +1))/2 — (75(75 + 1))/2 =
- (99(100))/2 — (75(76))/2 =
- 9900/2 — 5700/2 =
- 4950 — 2850 = 2100. Сумма чисел от 75 до 100 (без включения этих чисел) равна 2100.
- Пример. Найдем сумму («включительно») целых чисел от N 1 = 75 до N 2 = 100.
- 3 Уясните процесс. Представьте себе сумму целых чисел от 1 до 100 как 1 + 2 + 3 +.
 .. + 98 + 99 + 100 и сумму целых чисел от 1 до 75 как 1 + 2 + 3 + … + 73 + 74 + 75. Сумма целых чисел от 75 до 100 («включительно») есть вычисление: 75 + 76 + 77 + … + 99 + 100. Сумма чисел от 1 до 75 и сумма чисел от 1 до 100 равны до числа 75, но сумма чисел от 1 до 100 после числа 75 продолжается: … + 76 + 77 + … + 99 + 100. Таким образом, вычитая сумму чисел от 1 до 75 из суммы чисел от 1 до 100 мы «изолируем» сумму целых чисел от 75 до 100.
.. + 98 + 99 + 100 и сумму целых чисел от 1 до 75 как 1 + 2 + 3 + … + 73 + 74 + 75. Сумма целых чисел от 75 до 100 («включительно») есть вычисление: 75 + 76 + 77 + … + 99 + 100. Сумма чисел от 1 до 75 и сумма чисел от 1 до 100 равны до числа 75, но сумма чисел от 1 до 100 после числа 75 продолжается: … + 76 + 77 + … + 99 + 100. Таким образом, вычитая сумму чисел от 1 до 75 из суммы чисел от 1 до 100 мы «изолируем» сумму целых чисел от 75 до 100.- Если мы суммируем включительно, мы должны использовать сумму от 1 до 74, а не на сумму от 1 до 75, чтобы включить число 75 в конечную сумму.
- Аналогично, если мы суммируем без включения данных чисел, мы должны использовать сумму от 1 до 99, а не на сумму от 1 до 100, чтобы исключить число 100 из конечной суммы. Мы можем использовать сумму от 1 до 75, так как ее вычитание из суммы от 1 до 99 исключает число 75 из конечной суммы.
- В результате вычисления суммы всегда получается целое число, потому что либо N, либо N +1 – четное число, которое делится на 2 без остатка.

- Сумма = Сумма – Сумма.
- Другими словами: Сумма = n(n+1)/2
Предупреждения
- Хотя распространить этот метод на отрицательные числа не очень сложно, в данной статье рассматриваются только любые положительные целые числа N, где N больше или равно 1.
Цикл «Занимательная математика» посвящен деткам увлекающимся математикой и родителям, которые уделяют время развитию своих детей, «подкидывая» им интересные и занимательные задачки, головоломки.
Первая статья из этого цикла посвящена правилу Гаусса.
Немного истории
Известный немецкий математик Карл Фридрих Гаусс (1777-1855) с раннего детства отличался от своих сверстников. Несмотря на то, что он был из небогатой семьи, он достаточно рано научился читать, писать, считать. В его биографии есть даже упоминание того, что в возрасте 4-5 лет он смог скорректировать ошибку в неверных подсчетах отца, просто наблюдая за ним.
Одно из первых его открытий было сделано в возрасте 6 лет на уроке математики. Учителю было необходимо увлечь детей на продолжительное время и он предложил следующую задачку:
Учителю было необходимо увлечь детей на продолжительное время и он предложил следующую задачку:
Найти сумму всех натуральных чисел от 1 до 100.
Юный Гаусс справился с этим заданием достаточно быстро, найдя интересную закономерность, которая получила большое распространение и применяется по сей день при устном счете.
Давайте попробуем решить эту задачку устно. Но для начала возьмем числа от 1 до 10:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
Посмотрите внимательно на эту сумму и попробуйте догадаться, что же необычного смог разглядеть Гаусс? Для ответа необходимо хорошо представлять себе состав чисел.
Гаусс сгруппировал числа следующим образом:
(1+10) + (2+9) + (3+8) + (4+7) + (5+6)
Таким образом маленький Карл получил 5 пар чисел, каждая из которых в отдельности в сумме дает 11. Тогда, чтобы вычислить сумму натуральных чисел от 1 до 10 необходимо
Вернемся к первоначальной задаче. Гаусс заметил, что перед суммированием необходимо группировать числа в пары и тем самым изобрел алгоритм, благодаря которому можно быстро сложить числа от 1 до100:
1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100
Находим количество пар в ряде натуральных чисел. В данном случае их 50.
В данном случае их 50.
Суммируем первое и последнее числа данного ряда. В нашем примере — это 1 и 100. Получаем 101.
Умножаем полученную сумму первого и последнего члена ряда на количество пар этого ряда. Получаем 101 * 50 = 5050
Следовательно, сумма натуральных чисел от 1 до 100 равна 5050.
Задачи на использование правила Гаусса
А сейчас вашему вниманию предлагаются задачи, в которых в той или иной степени используется правило Гаусса. Эти задачки вполне способен понять и решить четвероклассник.
Можно дать возможность ребенку порассуждать самому, чтобы он сам «изобрел» это правило. А можно разобрать вместе и посмотреть как он сможет его применить. Среди ниже приведенных задач есть примеры, в которых нужно понять как модифицировать правило Гаусса, чтобы его применить к данной последовательности.
В любом случае, чтобы ребенок мог оперировать этим в своих вычислениях необходимо понимание алгоритма Гаусса, то есть умение разбить правильно по парам и посчитать.
Важно! Если будет заучена формула без понимания, то это очень быстро будет забыто.
Задача 1Найти сумму чисел:
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
- 1 + 2 + 3 + … + 14 + 15 + 16;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9;
- 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100.
Решение.
Вначале можно дать возможность ребенку самому решить первый пример и предложить найти способ, при котором это сделать легко в уме. Далее разобрать этот пример вместе с ребенком и показать как это сделал Гаусс. Лучше всего для наглядности записать ряд и соединить линиями пары чисел, дающие в сумме одинаковое число. Важно, чтобы ребенок понял как образуются пары — берем самое маленькое и самое большое из оставшихся чисел при условии, что количество чисел в ряду четно.
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = (1 + 10) * 5;
- 1 + 2 + 3 + … + 14 + 15 + 16 = (1 + 16) + (2 + 15) + (3 + 14) + (4 + 13) + (5 + 12) + (6 + 11) + (7 + 10) + (8 + 9) = (1 + 16) * 8 = 136;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) + (2 + 7) + (3 + 6) + (4 + 5) + 9 = (1+ 8) * 4 + 9 = 45;
- 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100 = (1 + 100) * 50 = 5050
Имеется 9 гирь весом 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г. Можно ли разложить эти гири на три кучки с равным весом?
Можно ли разложить эти гири на три кучки с равным весом?
Решение.
С помощью правила Гаусса находим сумму всех весов:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) * 4 + 9 = 45 (г)
Значит, если мы сможем сгруппировать гири так, чтобы в каждой кучке были гири суммарным весом 15г, то задача решена.
Один из вариантов:
- 9г, 6г
- 8г, 7г
- 5г, 4г, 3г, 2г, 1г
Другие возможные варианты найдите сами с ребенком.
Обратите внимание ребенка на то, что когда решаются подобные задачи лучше всегда начинать группировать с большего веса (числа).
Задача 3Можно ли разделить циферблат часов прямой линией на две части так, чтобы суммы чисел в каждой части были равны?
Решение.
Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим, делится ли она на 2:
Значит разделить можно. Теперь посмотрим как.
Следовательно, надо провести линию на циферблате так, чтобы 3 пары попали в одну половину, а три в другую.
Ответ: линия пройдет между числами 3 и 4, а затем между числами 9 и 10.
Задача 4Можно ли провести на циферблате часов две прямые линией так, чтобы в каждой части сумма чисел была одинаковой?
Решение.
Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим делиться ли она на 3:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78
78 делиться на 3 без остатка, значит разделить можно. Теперь посмотрим как.
По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:
1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.
Следовательно, надо провести линии на циферблате так, чтобы в каждую часть попали по 2 пары.
Ответ: первая линия пройдет между числами 2 и 3, а затем между числами 10 и 11; вторая линия — между числами 4 и 5, а затем между 8 и 9.
Летит стая птиц. Впереди одна птица (вожак), за ней две, потом три, четыре и т. д. Сколько птиц в стае, если в последнем ряду их 20?
Решение.
Получаем, что нам необходимо сложить числа от 1 до 20. А к вычислению такой суммы можно применить правило Гаусса:
1 + 2 + 3 + 4 + 5 + … + 15 + 16 + 17 + 18 + 19 + 20 = (20 + 1) * 10 = 210.
Задача 6Как рассадить 45 кроликов в 9 клеток так, чтобы во всех клетках было разное количество кроликов?
Решение.
Если ребенок решил и с пониманием разобрал примеры из задания 1, то тут же вспоминается, что 45 это сумма чисел от 1 до 9. Следовательно, сажаем кроликов так:
- первая клетка — 1,
- вторая — 2,
- третья — 3,
- восьмая — 8,
- девятая — 9.
Но если ребенок сразу не может сообразить, то попробуйте натолкнуть его на мысль о том, что подобные задачи можно решить перебором и надо начинать с минимального числа.
Вычислить сумму, используя прием Гаусса:
- 31 + 32 + 33 + … + 40;
- 5 + 10 + 15 + 20 + … + 100;
- 91 + 81 + … + 21 + 11 + 1;
- 1 + 2 + 3 + 4 + … + 18 + 19 + 20;
- 1 + 2 + 3 + 4 + 5 + 6;
- 4 + 6 + 8 + 10 + 12 + 14;
- 4 + 6 + 8 + 10 + 12;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11.
Решение.
- 31 + 32 + 33 + … + 40 = (31 + 40) * 5 = 355;
- 5 + 10 + 15 + 20 + … + 100 = (5 + 100) * 10 = 1050;
- 91 + 81 + … + 21 + 11 + 1 = (91 + 1) * 5 = 460;
- 1 + 2 + 3 + 4 + … + 18 + 19 + 20 = (1 + 20) * 10 =210;
- 1 + 2 + 3 + 4 + 5 + 6 = (1 + 6) * 3 = 21;
- 4 + 6 + 8 + 10 + 12 + 14 = (4 + 14) * 3 = 54;
- 4 + 6 + 8 + 10 + 12 = (4 + 10) * 2 + 12 = 40;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = (1 + 10) * 5 + 11 = 66.
Имеется набор из 12 гирек массой 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г, 10г, 11г, 12г. Из набора убрали 4 гирьки, общая масса которых равна трети общей массы всего набора гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?
Из набора убрали 4 гирьки, общая масса которых равна трети общей массы всего набора гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?
Решение.
Применяем правило Гаусса, чтобы найти общую массу гирек:
1 + 2 + 3 + … + 10 + 11 + 12 = (1 + 12) * 6 = 78 (г)
Вычисляем массу гирек, которые убрали:
Следовательно, оставшиеся гирьки (общей массой 78-26 = 52г) надо расположить по 26 г на каждую чашу весов, чтобы они оказались в равновесии.
Нам не известно какие гирьки были убраны, значит мы должны рассмотреть все возможные варианты.
Применяя правило Гаусса можно разбить гирьки на 6 пар с равным весом (по 13г):
1г и 12г, 2г и 11г, 3г и 10, 4г и 9г, 5г и 8г, 6г и 7г.
Тогда лучший вариант, когда при убирании 4 гирек уберутся две пары из приведенных выше. В этом случае у нас останутся 4 пары: 2 пары на одну чашу весов и 2 пары на другую.
Худший вариант — это когда 4 убранные гирьки разобьют 4 пары. У нас останутся 2 неразбитые пары общим весом 26г, значит их помещаем на одну чашу весов, а оставшиеся гирьки можно поместить на другую чашу весов и они тоже будут 26г.
У нас останутся 2 неразбитые пары общим весом 26г, значит их помещаем на одну чашу весов, а оставшиеся гирьки можно поместить на другую чашу весов и они тоже будут 26г.
Удачи в развитии Ваших детей.
1 + 2 + 3 + 4 +… / Хабр
Сумма всех натуральных чисел может быть записана с использованием следующего числового рядаЧему равна сумма этого бесконечного ряда? Перед тем, как читать дальше, дайте себе минуту на размышления. Если вы до этого не встречались с подобным рядом, а тема численных рядов в целом не слишком вам близка, то ответ на этот вопрос будет для вас большим сюрпризом.
Этот, на первый взгляд, совершенно противоречащий интуиции результат, тем не менее может быть строго доказан. Но прежде, чем говорить о доказательстве, нужно сделать отступление и вспомнить основные понятия.
Начнём с того, что «классической» суммой ряда называется предел частичных сумм ряда, если он существует и конечен. Подробности можно найти в википедии и соответствующей литературе. Если конечный предел не существует, то ряд называется расходящимся.
Если конечный предел не существует, то ряд называется расходящимся.
Например, частичная сумма первых k членов числового ряда 1 + 2 + 3 + 4 +… записывается следующим образом
Нетрудно понять, что эта сумма неограниченно растёт при стремлении k к бесконечности. Следовательно, исходный ряд является расходящимся и, строго говоря, не имеет суммы. Существует, однако, множество способов присвоить конечное значение расходящимся рядам.
Ряд 1+2+3+4+… далеко не единственный из расходящихся рядов. Возьмём, например, ряд Гранди
который тоже расходится, но известно, что метод суммирования Чезаро позволяет присвоить этому ряду конечное значение 1/2. Суммирование по Чезаро заключается в оперировании не частичными суммами ряда, а их арифметическими средними. Позволив себе порассуждать в вольном стиле, можно сказать, что то частичные суммы ряда Гранди осцилируют между 0 и 1, в зависимости от того какой член ряда является последним в сумме (+1 или -1), отсюда и значение 1/2, как арифметическое среднее двух возможных значений частичных сумм.
Другим интересным примером расходящегося ряда является знакопеременный ряд 1 — 2 + 3 — 4 +…, частичные суммы которого также осцилируют. Суммирование методом Абеля позволяет присвоить данному ряду конечное значение 1/4. Отметим, что метод Абеля является, своего рода, развитием метода суммирования по Чезаро, поэтому результат 1/4 несложно осмыслить с точки зрения интуиции.
Здесь важно отметить, что методы суммирования не являются трюками, которые придумали математики, чтобы как-то совладать с расходящимися рядами. Если вы примените суммирование по Чезаро или метод Абеля к сходящемуся ряду, то ответ, который дают эти методы, равен классической сумме сходящегося ряда.
Ни суммирование по Чезаро, ни метод Абеля, однако, не позволяют работать с рядом 1 + 2 + 3 + 4 +…, т. к. средние арифметические частичных сумм, равно как и средние арифметические средних арифметических, расходятся. Кроме того, если значения 1/2 или 1/4 ещё как-то можно принять и соотнести с соответствующими рядами, то -1/12 сложно связать с рядом 1 + 2 + 3 + 4 +. .., представляющим собой бесконечную последовательность положительных целых чисел.
.., представляющим собой бесконечную последовательность положительных целых чисел.
Существует несколько способов прийти к результату -1/12. В этой заметке я лишь кратко остановлюсь на одном из них, а именно регуляризации дзета-функцией. Введём дзета-функцию
Подставляя s = -1, получим исходный числовой ряд 1+2+3+4+…. Проделаем над этой функцией ряд несложных математических действий
Где является эта-функцией Дирихле
При значении s = -1 эта-функция становится уже знакомым нам рядом 1 — 2 + 3 — 4 + 5 -… «сумма» которого равна 1/4. Теперь мы можем легко решить уравнение
Интересно, что этот результат находит своё применение в физике. Например, в теории струн. Обратимся к стр. 22 книги Joseph Polchinski «String Theory»:
Если для кого-то теория струн не является убедительным примером в силу отсутствия доказательств множества следствий этой теории, то можно также упомянуть, что похожие методы фигурируют в квантовой теории поля при попытке рассчитать эффект Казимира.
Чтобы два раза не ходить, ещё пара интересных примеров с дзета-функцией
Для тех, кто захочет получить больше информации по теме отмечу, что написать данную заметку я решил после перевода соответствующей статьи на википедии, где в разделе «Ссылки» вы сможете найти массу дополнительного материала, в основном на английском языке.
выводит сумму чисел от 1 до n в python
GOAL: напишите программу, которая запрашивает у пользователя число n и выводит сумму
чисел от 1 до n. Программа продолжает запрашивать номер, пока
пользователь не введет 0.
expected output:
enter an integer number (0 to end): 5
1+2+3+4+5 = 15
Я могу решить вторую проблему, которая заключается в том, что пользователь вводит 0. проблема, с которой я столкнулся, заключается в том, что я печатаю числа в цикле.
1+2+3+4+5 = 15
Я думаю, что, возможно, если я использую цикл внутри цикла, я смогу достичь этого. Это мой текущий code.I’ve видел другие вопросы ответьте на этот вопрос программирования, но я хочу знать, как конкретно печатать числа, ведущие к номеру, который я ввел
Это мой текущий code.I’ve видел другие вопросы ответьте на этот вопрос программирования, но я хочу знать, как конкретно печатать числа, ведущие к номеру, который я ввел
num = int(input( "enter a integer: " ))
sum_num =0
if num != 0:
for i in range(1, num+1):
sum_num += i
print(sum_num)
else:
exit()
Поделиться Источник Angel Valenzuela 21 июня 2018 в 14:40
5 ответов
- Как найти сумму всех простых чисел меньше 1000 в Ruby?
Я новичок в Ruby. Я хочу знать, как получить сумму всех простых чисел ниже 1000. Приведенный ниже код выводит все простые числа от 1 до 1000. require ‘prime’ p = Prime.new (1..1000).each do |n| q = p.next() puts #{n}: #{q} end Как мне найти сумму этих простых чисел? Ценю вашу помощь
- Найдите сумму цифр всех чисел от 1 до N
Проблема: Найдите сумму цифр всех чисел от 1 до N (включая оба конца ) Временная сложность должна быть O (logN ) Для N = 10 сумма равна 1+2+3+4+5+6+7+8+9+(1+0) = 46 Для N = 11 сумма равна 1+2+3+4+5+6+7+8+9+(1+0)+(1+1) = 48 Для N = 12 сумма равна 1+2+3+4+5+6+7+8+9+(1+0)+(1+1) +(1+2)= 51 Это.
 ..
..
1
Я думаю, что это соответствует тому, что вы хотите:
while True:
output = ""
num = int(input("enter a integer: "))
if num == 0:
exit()
for i in range(1, num+1):
output += "{}".format(i)
if i != num:
output += "+"
output += " = {}".format(sum(range(num+1)))
print (output)
Это выводит сумму целых чисел, а затем ответ,а затем ждет следующего ввода. Пример вывода:
$ python test.py
enter a integer: 5
1+2+3+4+5 = 15
enter a integer: 4
1+2+3+4 = 10
enter a integer: 3
1+2+3 = 6
enter a integer: 2
1+2 = 3
enter a integer: 1
1 = 1
enter a integer: 0
= 0
Поделиться TobyGWilliams 21 июня 2018 в 15:01
1
Несколько проблем с вашим кодом:
- Ваш цикл
whileникогда не закончится. Его предназначение неясно.
Его предназначение неясно. - Вы суммируете 1 вместо
iкаждый раз в своем цикле. - Ваше утверждение
printвстречается только в конце. Вы можете включить его в свой цикл. - В Python
range(n)исключает n, поэтому вместо него используйтеrange(n + 1). - Вам не нужно преобразовывать целые числа в строку, чтобы получить
print.
Складывая все это вместе:
num = int(input( "enter a integer: " ))
sum_num = 0
for i in range(1, num+1):
sum_num += i
print(sum_num)
enter a integer: 5
1
3
6
10
15
Поделиться jpp 21 июня 2018 в 14:45
0
num=int(input("Enter the Number " ))
sum=0
for i in range(1, num + 1):
sum = sum+ i
print(sum)
Enter the Number 9
45
Поделиться Amit Kumar 02 апреля 2019 в 09:37
0
n = int(input("enter the no. : "))
sum = 0
for i in range(1,n+1):
if(i<n):
print(i,"+", end=" ")
else:
print(i,end=" ")
sum = sum + i
print("=",sum)
: "))
sum = 0
for i in range(1,n+1):
if(i<n):
print(i,"+", end=" ")
else:
print(i,end=" ")
sum = sum + i
print("=",sum)
Поделиться Jahanvi Verma 13 мая 2020 в 07:01
-1
n*(n+1)/2
«zBody zmust zbe zat zleast z30 zcharacters; zyou zentered z9 z…»
Поделиться Vlad K. 06 октября 2018 в 05:29
Похожие вопросы:
Найдите сумму всех чисел от 1 до N, делящихся либо на x, либо на y
Допустим, у нас есть 3 чисел N , x и y , которые всегда >=1 . N будет больше, чем x и y и x будет больше, чем y . Теперь нам нужно найти сумму всех чисел от 1 до N, которые делятся либо на x,…
spoj-CPCRC1C, сумма цифр чисел от 1 до n, нуждается в уточнении, а не в решении
Однажды учитель одного мальчика попросил его вычислить сумму чисел от 1 до n. мальчик быстро ответил, и Учитель бросил ему еще один вызов. Он попросил его вычислить сумму цифр чисел от 1 до n. Ввод…
мальчик быстро ответил, и Учитель бросил ему еще один вызов. Он попросил его вычислить сумму цифр чисел от 1 до n. Ввод…
Как найти сумму всех чисел от 1 до N с помощью JavaScript
Я пытаюсь найти способ вычислить сумму всех чисел от 1 до N, используя JavaScript. Ниже приведен код, который я пробовал до сих пор, но он, похоже, не работает. function numberSum(N) { var total =…
Как найти сумму всех простых чисел меньше 1000 в Ruby?
Я новичок в Ruby. Я хочу знать, как получить сумму всех простых чисел ниже 1000. Приведенный ниже код выводит все простые числа от 1 до 1000. require ‘prime’ p = Prime.new (1..1000).each do |n| q =…
Найдите сумму цифр всех чисел от 1 до N
Проблема: Найдите сумму цифр всех чисел от 1 до N (включая оба конца ) Временная сложность должна быть O (logN ) Для N = 10 сумма равна 1+2+3+4+5+6+7+8+9+(1+0) = 46 Для N = 11 сумма равна…
Напишите рекурсивную функцию, которая вычислит сумму всех чисел от 1 до n-swift
Что я могу поместить в эту функцию, чтобы вычислить сумму чисел от 1 до n в swift? func sumOfNumbersRecursive(n: Int) -> Int { if (n == 0) { } else { //recursive } } Спасибо
Сумма от 1 до n в одной строке Python
Учитывая число n , мне нужно найти сумму чисел от 1 до n . Пример ввода и вывода: 100 5050 Поэтому я придумал print(sum(range(int(input())+1))) , который решает проблему в одной строке, но занимает…
Пример ввода и вывода: 100 5050 Поэтому я придумал print(sum(range(int(input())+1))) , который решает проблему в одной строке, но занимает…
Подсчитайте, сколько чисел было суммировано от 1 до n
У меня есть математический вопрос. Имея сумму чисел от 1 до n. Например это может быть: sum([i for i in range(46)]) Так что в сумме составляет 1035. Теперь мой вопрос заключается в том, что мы знаем…
Найти сумму квадратов чисел от 1 до N? (Без предыдущей суммы)
Программа, которую я написал, имеет список нечетных чисел слева от 5 до 49, в то время как правый столбец имеет сумму квадратов от 1 до N (число слева). Проблема с моим кодом заключается в том, что…
Сумма всех простых чисел от 1 до N в Python
Я новичок в программировании. Пытаясь решить эту проблему, я получаю неправильный ответ. Я несколько раз проверил свой код, но так и не смог понять, в чем ошибка. Пожалуйста, помогите мне решить эту…
Решение задач на Питоне.
 Сумма ряда натуральных чисел
Сумма ряда натуральных чисел Попробуем на практике разобрать работу циклов, про которые рассказано в одном из наших уроков. Выполним предложенное задание, использовав несколько разных методик и видов циклов.
Задача
Программа выводит сумму первых членов натурального ряда чисел до введённого n-числа включительно.
Решение задачи с помощью цикла while
Произведём расчёт, используя цикл с предусловием while.
n=int(input(Введите последнее число из ряда натуральных чисел=))
i=1
s=0
while i s=i+s
i=i+1
print (Сумма чисел от 1 до, n, =, s)
- Сперва задаем в переменную n самое большое натуральное число (в пределах разумного).
- Обнулим на входе сумму s.
- Цикл будет выполняться до тех пор, пока внутренняя переменная не достигнет значения n.
Результат выполнения программы
Решение задачи с помощью цикла for
Быстрее происходит расчёт при помощи цикла for.
n=int(input(Введите последнее число=))
s=0
for i in range(1,n+1):
s=i+s
print (Сумма чисел от 1 до, n, =, s)
Посмотрите, в цикле записано максимальное число не n, а n+1. Это связано с тем, что цикл должен выполняться на один шаг больше, чтобы последнее значение промежуточной суммы было учтено.
Результат выполнения программы
Решение задачи с помощью списка
Ту же самую задачку можно решить, используя список. По сути, это ничего не меняет, но, как видите, код при этом занимает всего две строки:
n=int(input(Введите последнее число=))
print (Сумма чисел от 1 до, n, =, sum([i for i in range(1,n+1)]))
Результат выполнения программы
Задача на последовательность Функция перевода целого двоичного числа в десятичное
|
| ||||||||||||||||||||||||||||||||||||||||
Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессия не будет для Вас сложной темой после просмотра следующих примеров. Внимательно ознакомьтесь с ответами среднего уровня сложности и выберите для себя самое необходимое. Если приведенные примеры для Вас тяжелые, прочитайте для начала простые примеры на арифметическую и геометрическую прогрессию (1 уровень).
Группа Б (уровень 2)
Пример 1. В арифметической прогрессии а8=12,4; a23=4,7. Вычислить сумму а14+a17.
Решение: Представим 14 член прогрессии через 8 и 17 через 23. В виде формул они будут запись
a14=а8+6d;
a17=a23-6d.
Находим искомую сумму членов прогрессии
a14+a17=a8+6d+a23-6d=a8+a23;
a14+a17=12,4+4,7=17,1. 2+6*2=24.
2+6*2=24.
Из второго уравнения, учитывая значение первого члена, находим шаг прогрессии
d=24-2a1=24-2*9=6.
По общей формуле вычисляем 6 член арифметической прогрессии
a6=a1+5d=9+5*6=39.
Ответ: a6=39.
Пример 4. Сумма п первых членов арифметической прогрессии выражается формулой Sn=n2+5n. Вычислить a10.
Решение: Задача идентичное предыдущей, только на этот раз попробуем решить по другой методике. Используем сумму арифметической прогрессии в виде
Подставим в эту формулу заданную зависимость суммы и приравняем коэффициенты при одинаковых степенях n
Это и есть важная формула, из которой находим первый член прогрессии и разность (шаг)
d=2; a1=5+d/2=6.
Вычисляем 10 член прогрессии
a10=a1+9d=6+9*2=24.
Ответ: a10=24.
Пример 5. Вычислить сумму всех четных натуральных чисел до 100 включительно.
Решение: Первый элемент последовательности равен a1=2, последний равен 100. От 1 до 10 имеем 5 четных чисел. В сотни всего 10 десятков то есть 10*5 четных чисел. Если рассуждать по-другому, то половина элементов до 100 четные, половина — нечетные.
100/2=50 – количество четных чисел.
Разница прогрессии равна 2.
Далее подставляем известные значения в формулу и вычисляем
Сумма четных чисел до 100 равна 2550.
Ответ: S50=2550.
Пример 6. Вычислить сумму всех двузначных чисел.
Решение: Номер члена прогрессии будет равен его значению
a1=1;… a99=99.
Разница прогрессии равна единице d=1. Находим сумму арифметической прогрессии по формуле
Сумма равна 4950.
Ответ: S99=4950.
Пример 7. В арифметической прогрессии а2+a11=10, а5+a6=13. Вычислить разницу прогрессии.
Решение: Аглоритм решения подобных примеров следующий: Выражаем члены прогрессии через один, имеющий наименьший порядковый номер
a11=a2+9d;
a5=a2+3d;
a6=a2+4d.
Подставляем ету запись в сумму членов прогрессии
a2+a2+9d=2*a2+9d=10;
a2+3d+a2+4d=2*a2+7d=13.
Есть два уравнения с двумя неизвестными. Для отыскания разницы прогрессии от первого уравнения вычитаем второе
9d-7d=2d=10-13;
2d=-3; d=-1,5.
Ответ: d=-1,5.
Пример 8. В арифметической прогрессии а2+a11=10, а5+a6=13. Вычислить a1.
Решение: Задача аналогична предыдущей. Выражаем, для удобства, все члены суммы через 1 номер
a2=a1+d; a11=a1+10d;
a5=a1+4d; a6=a1+5d.
Подставляем в формулы и составляем уравнение
a1+d+a1+10d=2*a1+11d=10;
a1+4d+a1+5d=2*a1+9d=13.
От первого уравнения вычтем второе и найдем шаг прогрессии
11d-9d=2d=10-13=-3.
2d=-3; d=-1,5.
Зная шаг прогрессии, первый ее элемент находим из уравнения
2*a1+9*(-1,5)=13; 2*a1=13+13,5=26,5;
a1=26,5/2=13,25.
Ответ: a1=13,25.
Пример 9. Вычислить сумму всех двузначных натуральных чисел которые при делении на 3 дают в остатка 2.
Решение: Сначала запишем общую формулу члена прогрессии для данной задачи. Учитывая условие получим зависимость
a[n]=3*n+2.
Первое двузначное число, которое удовлетворяет условию это 11.
a[3]=3*3+2=11.
Последнее число равно 98 и оно соответствует 32 номеру прогрессии
a[32]=3*32+2=98.
Дальше есть выбор из двух вариантов — искать частичную сумму прогрессии или от полной суммы вычесть первых два элемента. Поступим по второй схеме
a1=3+2=5; a2=3*2+2=8;
От найденной суммы вычитаем первые два элемента прогрессии
S=1648-5-8=1635.
Ответ: S=1635.
Пример 10. Вычислить сумму всех двузначных натуральных чисел которые при делении на 4 дают в остатка 1.
Решение: Выпишем общую формулу члена прогрессии
a[n]=4*n+1.
Всегда поступайте таким образом для описания прогрессии.
Первое нужное число равно 13. Его легко получить взяв несколько членов прогрессии – 5; 9;13; …
С последним номером немного больше поисков, но можно установить, что это будет 97.
a[3]=13; a[24]=97.
Шаг прогрессии составляет d=4.
Находим сумму двузначных натуральных чисел
Получили в сумме 1210.
Ответ: S=1210.
Пример 11. Вычислить сумму всех нечетных натуральных чисел от 13до 81 включительно.
Решение: Запишем формулу нечетных чисел.
a[n]=2*n+1, n=0; 1; …
Сделаем замену в прогрессии так, чтобы элемент под первым номером был равен 13.
a[n]=2*n+1=13.
Отсюда n=6. Значит новая прогрессия выходит с предыдущей добавлением к индексу n+1=6; n=5.
b[n]=2(n+5)+1.
Найдем под каким номером в прогрессии идет число 81.
2*(n+5)+1=81;
n+5=(81-1)/2=40; n=35.
Итак b[35]=81.
Находим сумму первых 35 членов прогрессии
Следовательно, искомая сумма равна 1645.
Второй метод заключается в нахождении суммы прогрессии a[n] с определенного ее номера. Для этого нужно знать формулу, которую порой нет возможности на контрольных или тестах выводить из формулы суммы прогрессии
Если Вы ее знаете, то в этом случае нужную найти сумму от 6 до 40 члена прогрессии a[n]
И на «закуску» третий способ, который заключается в вычитании из полной суммы прогрессии суммы ее первых членов.
На этом вычисления примера завершены.
Ответ: S=1645.
Пример 12. В арифметической прогрессии а18=12,3; a32=2,8. Вычислить а21+a29.
Решение: Если Вы внимательно просмотрели ответы в предыдущих примерах то знаете как поступить в этом задании. Сначала выражаем 21 и 29 член прогрессии через 18 и 32.
a21=a18+(21-18)d=a18+3d;
a29=a32+(29-32)d=a32-3d.
Легко видеть, что при суммировании разница прогрессии пропадает
a21+a29=a18+a32=12,3+2,8=15,1.
Ответ: сумма равна 15,1.
Пример 13. Сумма п первых членов арифметической прогрессии выражается формулой Sn=13n2+5n. Вычислить разницу прогрессии.
Решение: Подобная задача рассматривали под номером 3, 4. Запишем общую формулу суммы прогрессии и приравняем к заданной
Приравняем коэффициенты при квадрате номера прогрессии
Разница прогрессии равна 26
Ответ: d=26.
Пример 14 Сумма п первых членов арифметической прогрессии выражается формулой Sn=3n2+8n. Вычислить разницу прогрессии.
Решение: Здесь не будем Вас утомлять и по аналогии с предыдущим примером запишем, что коэффициент при квадрате индекса равен половине разницы прогрессии
d/2=3; d=3*2=6.
Видим, наскоько просто найти разницу прогрессии.
Ответ: d=6.
Пример 15. В геометрической прогрессии bm-n=7,2; bm=9,6. Вычислить bm+n
Решение: На вид задания на геометрическую прогрессию сложное. n.
n.
Выполним соответствующие расчеты
b[m-n]=4,2*4,2/6,3=2,8.
Ответ: b[m-n]=2,8.
Пример 17. В арифметической прогрессии ат+п=1,4; ат-п=92,8. Вычислить ат.
Решение: Неизвестный член арифметической прогрессии равен среднему арифметическому соседних элементов. Поскольку ат+п и ат-п есть равноудалены елементами прогрессии от ат , то его находим по формуле
a[m]=(92,8+1,4)/2=47,1.
Ответ a[m]=47,1.
Пример 18. В арифметической прогрессии ат =8,75; ат+п=13,8. Вычислить a[m-n]
Решение: Выразим следующие члены прогрессии через предыдущие
a[m+n]=a[m]+n*d;
a[m]=a[m-n]+ n*d.
С первой формулы находим произведение n*d и подставляем во вторую
n*d= a[m+n]-a[m];
a[m-n]=a[m]-n*d=2*a[m]-a[m+n].
Подставим значение в формулу и найдем нужный элемент прогрессии
a[m-n]= 2*8,75-13,8=3,7.
Ответ: a[m-n]=3,7.
Пример 19. В геометрической прогрессии b21*b7=62,7. Вычислить b19 если b9=5,5.
В геометрической прогрессии b21*b7=62,7. Вычислить b19 если b9=5,5.
Решение: Задача одна из сложных среди всех которые рассмотренные здесь, однако на практике решить возможно. Запишем все старшие члены геометрической прогрессии через b7
Запишем произведение 21 и 7 члена геометрической прогрессии и расписано b9
Чтобы получить выражение для 19 члена прогрессии нужно произведение b21*b7 разделить на b9
С опытом Вы увидите, что в подобных примерах остается делить одни значения на вторые или умножать, примеры где нужно тянуть корни или подносить к степени в геометрических прогрессиях встречаются крайне редко.
Вычисляем b19
b[19]=62,7/5,5=11,4.
Ответ: b[19]=11,4.
Пример 20. Вычислить сумму первых двадцати членов арифметической прогрессии (аn) если а6 +а9+а12+ а15 = 20 .
Решение: Выглядит на первый взгляд непонятно, как с такой записи получить сумму. Однако, если вспомнить формулу суммы арифметической прогрессии, то все что там фигурирует — это первый и последний член суммы, а также их количество. Таким образом следует представить сумму заданных членов прогрессии через первый и последний элемент. Уверяю Вас, что разница прогрессии в расчетах упростится и заданное условие не что иное, как удвоенная сумма первого и 20 члена прогрессии. В этом Вы сейчас наглядно убедитесь. Расписываем первые два слагаемые суммы через a [1], а остальные через a[20].
Однако, если вспомнить формулу суммы арифметической прогрессии, то все что там фигурирует — это первый и последний член суммы, а также их количество. Таким образом следует представить сумму заданных членов прогрессии через первый и последний элемент. Уверяю Вас, что разница прогрессии в расчетах упростится и заданное условие не что иное, как удвоенная сумма первого и 20 члена прогрессии. В этом Вы сейчас наглядно убедитесь. Расписываем первые два слагаемые суммы через a [1], а остальные через a[20].
a[6]=a[1]+5d;
a[9]=a[1]+8d;
a[12]=a[20]-8[d];
a[15]=a[20]-5d.
Просуммировав их всех получим
a[6]+a[9]+a[12]+a[15]=2*a1+2*a[20].
Формула суммы 20 членов арифметической прогрессии имеет вид
Числитель дроби и является заданной суммой, разделенной на 2 Поэтому сразу выполняем вычисления
S[20]=20/2/2*20=100.
Ответ: S[20]=100.
Пример 21. Сумма первого и пятого членов арифметической прогрессии равна 28,а произведение четвертого и третьего членов 280. Вычислить сумму первых десяти членов прогрессии.
Вычислить сумму первых десяти членов прогрессии.
Решение: В этом задании и подобных нужно составлять систему уравнений. Для этого запишем сначала условие задания в виде
a[1]+a[5]=28; a[3]*a[4]=28.
Поскольку 3 член прогрессии является равноудален от 1 и 5, то их среднее арифметическое и будет 3 членом прогрессии
a[3]=(a[1]+a[5])/2=28/2=14.
Произведение распишем через 3 член прогрессии
a[3]*a[4]=a[3]*(a[3]+d)=280;
14*(14+d)=280.
Отсюда находим разницу прогрессии
14+d=280/14=20;
d=20-14=6.
Вычислим 1 и 10 член арифметической прогрессии
a[1]=a[3]-2d=14-2*6=2;
a[10]=a[3]+7d=14+7*2=28.
Есть все необходимые елементы для вычисления суммы прогрессии
S[10]=(2+28)*10/2=150.
Ответ: S[10]=150.
Пример 22. Знайты четыре числа которые образуют геометрическую прогрессию в которой третий член больше первого на 9, а второй больше четвертого на 18. В ответе записать их сумму.
Решение: Запишем условие задачи в виде
b[3]-b[1]=9; b[2]-b[4]=18.
Распишем члены геометрической прогрессии через 1 элемент
Поделив второе уравнения на первое получим знаменатель прогрессии
Из первого уравнения находим 1 член геометрической прогрессии
Все остальные члены прогрессии получаем умножением предыдущего номера на знаменатель.
b[2]=b[1]*q=3*(-2)=-6;
b[3]=b[2]*q=-6*(-2)=12;
b[4]=12*(-2)=-24.
Осталось вычислить сумму членов геометрической прогрессии
S=3-6+12-24=-15.
Ответ: S=-15.
Пример 23. Знаменатель геометрической прогрессии 1/3, третий член геометрической прогрессии 1/9, а сумма всех членов геометрической прогрессии 13/9. Найти количество членов геометрической прогрессии.
Решение: Сумма членов геометрической прогрессии находим по формуле
Найдем первый член прогрессии через 3 и знаменатель.
Подставим значение в формулу суммы и найдем количество суммируемых членов
Итак, получили 3 члена геометрической прогрессии.
Ответ: n=3.
Пример 24. Дано две арифметические прогрессии. Первый и пятый члены первой прогрессии соответственно равны 7 и -5. Первый член второй прогрессии равна 0, а последний 7/2. Вычислить сумму членов второй прогрессии если известно,что третьи члены обеих прогрессий равны между собой.
Дано две арифметические прогрессии. Первый и пятый члены первой прогрессии соответственно равны 7 и -5. Первый член второй прогрессии равна 0, а последний 7/2. Вычислить сумму членов второй прогрессии если известно,что третьи члены обеих прогрессий равны между собой.
Решение: Запишем условие примера
a[1]=7;a[5]=-5;
b[1]=0; b[n]=7/2;
a[3]=b[3]; S[n]-?
Найдем 3 член первой прогрессии через среднее арифметическое соседних
a[3]=(a[1]+a[5])/2=(7-5)/2=1.
Учитывая что
b[3]=a[3]=1,
найдем шаг второй прогрессии.
b[3]=b[1]+2*d;
1=0+2*d; d=1/2=0,5.
Найдем номер последнего члена второй прогрессии
b[n]=0+(n-1)d=7/2=3,5;
n-1=3,5/d=3,5/0,5=7;
n=7+1=8.
Вычислим сумму восьми членов прогрессии
S[8]=(0+3,5)*8/2=3,5*4=14.
Ответ: S[8]=14.
После такой практиктики я думаю Вы знаете как находить сумму арифметической и геометрической прогрессии. Если нет ознакомьтесь с примерами изначально (это была шутка).
Похожие материалы:
Если примеры были полезны Вам — посоветуйте их друзьям.
Калькулятор расчета сумм последовательностей | BBF.RU
Последовательность — высокоупорядоченный числовой набор, образованный по заданному закону. Термин «ряд» обозначает результат сложения членов соответствующей ему последовательности. Для различных числовых последовательностей мы можем найти сумму всех ее членов или общее число элементов до заданного предела.
Последовательность
Под этим термином понимается заданный набор элементов числового пространства. Каждый математический объект задается определенной формулой для определения общего элемента последовательности, а для большинства конечных числовых наборов существуют простые формулы определения их суммы. Наша программа представляет собой сборник из 8 онлайн-калькуляторов, созданных для вычисления сумм наиболее популярных числовых наборов. Начнем с самого простого — натурального ряда, которым мы пользуемся в повседневной жизни для пересчета предметов.
Натуральная последовательность
Когда школьники изучают числа, они первым делом учатся считать предметы, например, яблоки. Натуральные числа естественным образом возникают при счете предметов, и каждый ребенок знает, что 2 яблока — это всегда 2 яблока, не больше и не меньше. Натуральный ряд задается простым законом, который выглядит как n. Формула гласит, что n-ный член числового набора равен n: первый — 1, второй — 2, четыреста пятьдесят первый — 451 и так далее. Результат суммирования n первых натуральных чисел, то есть начинающихся от 1, определяется по простой формуле:
Натуральные числа естественным образом возникают при счете предметов, и каждый ребенок знает, что 2 яблока — это всегда 2 яблока, не больше и не меньше. Натуральный ряд задается простым законом, который выглядит как n. Формула гласит, что n-ный член числового набора равен n: первый — 1, второй — 2, четыреста пятьдесят первый — 451 и так далее. Результат суммирования n первых натуральных чисел, то есть начинающихся от 1, определяется по простой формуле:
∑ = 0,5 n × (n+1).
Благодаря этому выражению легко рассчитать конечную сумму натурального ряда от 1 до n. Очевидно, что натуральная последовательность стремится в бесконечность, поэтому, чем больше n, тем больше конечный результат.
Расчет суммы натурального ряда
Для вычислений вам потребуется выбрать в меню калькулятора формулу натурального ряда n и ввести количество членов последовательности. Давайте вычислим сумму натурального ряда от 1 до 15. Указав n = 15, вы получите результат в виде самой последовательности:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
и суммы натурального ряда, равной 120.
Легко проверить корректность вычислений при помощи выше приведенной формулы. Для нашего примера результат сложения будет равен 0,5 × 15 × 16 = 0,5 × 240 = 120. Все верно.
Последовательность квадратов
Квадратичная последовательность образуется из натуральной, путем возведения каждого члена в квадрат. Ряд квадратов формируется по закону n2, следовательно, n-ный член последовательности будет равняться n2: первый — 1, второй — 22 = 4, третий — 32 = 9 и так далее. Результат суммирования начальных n элементов квадратичной последовательности вычисляется по закону:
∑ = (n × (n+1) × (2n+1)) / 6.
При помощи этой формулы вы легко можете высчитать сумму квадратов от 1 до n для сколько угодно большого n. Очевидно, что эта последовательность также бесконечна и с ростом n будет расти и общее значение числового набора.
Расчет суммы квадратного ряда
В этом случае вам потребуется выбрать в меню программы закон квадратной последовательности n2, после чего выбрать значение n. Давайте рассчитаем сумму первых десяти членов последовательности (n= 10). Программа выдаст саму последовательность:
Давайте рассчитаем сумму первых десяти членов последовательности (n= 10). Программа выдаст саму последовательность:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100
а также сумму, равную 385.
Кубический ряд
Ряд кубов представляет собой последовательность натуральных чисел, возведенных в куб. Закон образования общего элемента последовательности записывается как n3. Таким образом, первый член ряда равен 13 = 1, второй — 23 = 8, третий — 33 = 27 и так далее. Сумма первых n элементов кубического ряда определяется по формуле:
∑ = (0,5 n × (n+1))2
Как и в предыдущих случаях, элементы числового пространства стремятся в бесконечность, и чем больше количество слагаемых, тем больше результат суммирования.
Расчет суммы кубического ряда
Для начала выберите в меню калькулятора закон кубического ряда n3 и задайте любое значение n. Давайте определим сумму ряда из 13 членов. Калькулятор выдаст нам результат в виде последовательности:
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197
и суммы соответствующего ей ряда, равного 8281.
Последовательность нечетных чисел
Множество натуральных чисел содержит подмножество нечетных элементов, то есть тех, которые не делятся на 2 без остатка. Последовательность нечетных чисел определяется выражением 2n — 1. Согласно закону, первый член последовательности будет равен 2×1 − 1 = 1, второй — 2×2 − 1 = 3, третий — 2×3 − 1 = 5 и так далее. Сумма начальных n элементов нечетного ряда вычисляется по простой формуле:
∑ = n2.
Рассмотрим пример.
Вычисление суммы нечетных чисел
Сначала выберете в меню программы закон образования нечетного ряда 2n−1, после чего введите n. Давайте узнаем первые 12 членов нечетной ряда и его сумму. Калькулятор мгновенно выдаст результат в виде набора чисел:
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23,
а также суммы нечетного ряда, который равен 144. И действительно, 122 = 144. Все верно.
Прямоугольные числа
Прямоугольные числа относятся к классу фигурных чисел, которые представляют собой класс числовых элементов, необходимых для построения геометрических фигур и тел. К примеру, чтобы построить треугольник необходимо 3, 6 или 10 точек, квадрат — 4, 9 или 16 точек, а для выкладывания тетраэдра потребуется 4, 10 или 20 шаров или кубов. Прямоугольники легко построить при помощи двух последовательных чисел, например, 1 и 2, 7 и 8, 56 и 57. Прямоугольные же числа выражаются в виде произведения двух последовательных натуральных чисел. Формула для общего члена ряда выглядит какn × (n+1). Первые десять элементов такого числового набора выглядят как:
К примеру, чтобы построить треугольник необходимо 3, 6 или 10 точек, квадрат — 4, 9 или 16 точек, а для выкладывания тетраэдра потребуется 4, 10 или 20 шаров или кубов. Прямоугольники легко построить при помощи двух последовательных чисел, например, 1 и 2, 7 и 8, 56 и 57. Прямоугольные же числа выражаются в виде произведения двух последовательных натуральных чисел. Формула для общего члена ряда выглядит какn × (n+1). Первые десять элементов такого числового набора выглядят как:
2, 6, 12, 20, 30, 42, 56, 72, 90, 110…
С увеличением n растет и значение прямоугольных чисел, следовательно, сумма такого ряда также будет расти.
Обратная последовательность
Для прямоугольных чисел существует обратная последовательность, определяемая формулой 1 / (n × (n+1)). Числовой набор трансформируется в набор дробей и выглядит как:
1/2 , 1/6, 1/12, 1/20, 1/30, 1/42, 1/56, 1/72, 1/90, 1/110…
Сумма ряда дробей определяется по формуле:
∑ = 1 — 1/(n+1).
Очевидно, что при увеличении количества элементов ряда значение дроби 1/(n+1) стремится к нулю, а результат сложения приближается к единице. Рассмотрим примеры.
Рассмотрим примеры.
Сумма прямоугольного и обратного ему ряда
Давайте рассчитаем значение прямоугольной последовательности для n = 20. Для этого выберете в меню онлайн-калькулятора закон задания общего члена числового набора n × (n+1) и укажите n. Программа выдаст мгновенный результат в виде 3080. Для вычислений обратного ряда измените закон на 1 / (n × (n+1)). Сумма обратных числовых элементов будет равна 0,952.
Ряд произведений трех последовательных чисел
Прямоугольный числовой набор можно изменить, добавив к нему еще один последовательный множитель. Следовательно, формула для вычисления n-ного члена набора преобразится в n × (n+1) × (n+2). Согласно этой формуле элементы ряда образуются в виде произведения трех последовательных чисел, например, 1 × 2 × 3 или 10 × 11 × 12. Первые десять элементов такого ряда выглядят как:
6, 24, 60, 120, 210, 336, 504, 720, 990, 1320
Это быстрорастущий числовой набор, а сумма соответствующего ряда при росте n уходит в бесконечность.
Обратная последовательность
Как и в предыдущем случае, мы можем обратить формулу n-ного члена и получить выражение 1 / (n × (n+1) × (n+2)). Тогда набор целых значений преобразится в ряд дробей, в знаменателе которых будут стоять произведения трех последовательных чисел. Начало такого набора имеет следующий вид:
1/6, 1/24, 1/60, 1/120, 1/210, 1/336…
Сумма соответствующего ряда определяется по формуле:
∑ = 0,5 × (0,5 — 1 / (n+1) × (n+2)).
Очевидно, что при росте количества элементов дробь 1 / ((n+1) × (n+2)) стремится к нулю, а сумма ряда приближается к значению 0,5 × 0,5 = 0,25. Рассмотрим примеры.
Ряд произведений трех последовательных чисел и обратный ему
Для работы с этим набором требуется выбрать закон определения общего элемента n × (n+1) × (n+2) и задать n, к примеру, 100. Калькулятор выдаст вам саму последовательность, а также значение результата сложения сотни чисел, равный 26 527 650. Если выбрать обратный закон 1 / (n × (n+1) × (n+2)), сумма ряда из 100 членов будет равна 0,250.
Заключение
Сборник калькуляторов позволяет рассчитать сумму восьми наиболее популярных последовательностей. Пользуйтесь нашим сервисом для решения учебных заданий по математике или программированию.
он жеmathschallenge.net
Часто задаваемые вопросы
Есть ли формула для сложения последовательности кубиков?
Изучив первые пять сумм, можно сделать замечательное открытие:
1 3 = 1
1 3 +2 3 = 9
1 3 +2 3 +3 3 = 36
1 3 +2 3 +3 3 +4 3 = 100
1 3 +2 3 +3 3 +4 3 +5 3 = 225
Кажется, что сумма всегда квадратная, но еще более примечательно то, что сумма первых n кубов, 1 3 +2 3 +… + n 3 = ( n ( n +1) / 2) 2 , который является квадратом числа треугольника n th .
Например, 1 3 +2 3 + … + 10 3 = (10 × 11/2) 2 = 55 2 = 3025.
Используя аналогичный метод, использованный для доказательства этой формулы для суммы квадратов, мы докажем этот результат дедуктивно; есть надежда, что это даст некоторое представление о том, как дальше может быть найден ряд способностей.
Проба
| r 4 — ( r –1) 4 | = | n 4 — ( n –1) 4 + ( n –1) 4 — ( n –2) 4 + … + 3 4 — 2 4 + 2 4 –1 4 + 1 4 –0 4 | |
| = | n 4 |
Но r 4 — ( r –1) 4 = r 4 — ( r 4 –4 r 3 +6 r 2 –4 r +1) = 4 r 3 –6 r 2 +4 r –1.
| ∴ ∑ 4 r 3 –6 r 2 +4 r –1 | = | 4∑ r 3 — 6∑ r 2 + 4∑ r — ∑1 |
| = | 4∑ r 3 — 6 n ( n +1) (2 n +1) / 6 + 4 n ( n +1) / 2 — n | |
| = | 4∑ r 3 — n ( n +1) (2 n +1) + 2 n ( n +1) — n | |
| = | № 4 . |
| ∴ 4∑ r 3 | = | n 4 + n ( n +1) (2 n +1) — 2 n ( n +1) + n |
| = | n ( n 3 + ( n +1) (2 n +1) — 2 ( n +1) + 1 | |
| = | n ( n 3 + 2 n 2 +3 n +1 — 2 n –2 + 1) | |
| = | n ( n 3 +2 n 2 + n ) | |
| = | n 2 ( n 2 +2 n +1) | |
| = | n 2 ( n +1) 2 | |
| ∴ ∑ r 3 | = | n 2 ( n +1) 2 /4 |
| = | ( n ( n +1) / 2) 2 |
Другими словами, сумма первых n кубиков является квадратом суммы первых n натуральных чисел.
Программа Python для поиска суммы первых N натуральных чисел
Это программа на языке Python для нахождения суммы первых N натуральных чисел.
Описание проблемы
Программа берет количество членов и находит сумму первых N натуральных чисел.
Решение проблемы
1. Возьмите количество натуральных чисел, которое нужно найти, и сохраните его в отдельной переменной.
2. Инициализируйте переменную суммы до 0.
3. Используйте цикл while, чтобы найти сумму натуральных чисел и уменьшить число для каждой итерации.
4. Числа добавляются к переменной суммы, и так продолжается до тех пор, пока значение числа не станет больше 0.
5. Затем выводится сумма первых N натуральных чисел.
6. Выход.
Программа / исходный код
Вот исходный код программы Python для нахождения суммы первых N натуральных чисел. Вывод программы также показан ниже.
n = int (input ("Введите число:"))
сумма1 = 0
в то время как (n> 0):
сумма1 = сумма1 + п
п = п-1
print ("Сумма первых n натуральных чисел равна", sum1) Описание программы
1. Пользователь должен ввести количество натуральных чисел, чтобы найти сумму.
Пользователь должен ввести количество натуральных чисел, чтобы найти сумму.
2. Переменная sum инициализируется значением 0.
3. Цикл while используется для нахождения суммы натуральных чисел, и число уменьшается для каждой итерации.
4. Числа добавляются к переменной суммы, и это продолжается до тех пор, пока значение переменной не станет больше 0.
5. Когда значение переменной станет меньше 0, печатается общая сумма N натуральных чисел.
Случаи тестирования
Случай 1: Введите число: 18 Сумма первых n натуральных чисел равна 171. Случай 2: Введите номер: 167 Сумма первых n натуральных чисел равна 14028
Серия Sanfoundry Global Education & Learning — Программы Python.
Чтобы попрактиковаться во всех программах Python, — это полный набор из 150+ проблем и решений Python .
Примите участие в конкурсе сертификации Sanfoundry и получите бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!Суммируйте нечетные числа от 1 до 100
На прошлой неделе на форумах Chandoo. org, Сунита , задала вопрос:
org, Сунита , задала вопрос:
«Пожалуйста, помогите мне узнать сумму нечетных чисел в диапазоне от 1 до 100 чисел
Нравится 1 + 3 + 5 + 7 +… 97+ 99
Как найти с помощью формулы Excel? »
Я использовал две формулы массива:
= СУММ (2 * СТРОКА (СМЕЩЕНИЕ ($ A $ 1 ,,, 100/2)) — 1) Ctrl Shift Enter
и
= СУММ (СТРОКА (1: 100) * МОД (СТРОКА (1: 100), 2)) Ctrl Shift Enter
Давайте рассмотрим каждый из них по очереди.
Как обычно, на сайте Formula Forensics вы можете скачать образец файла здесь, а затем загрузить образец файла.
Формула 1: = СУММ (2 * СТРОКА (СМЕЩЕНИЕ ($ A $ 1 ,,, 100/2)) — 1)
Первая формула, которую мы рассмотрим:
= СУММ (2 * СТРОКА (СМЕЩЕНИЕ ($ A $ 1 ,,, 100/2)) — 1) Ctrl Shift Enter
Эта формула работает по принципу создания массива нечетных чисел от 1 до 100 и их сложения.
Мы можем составить массив нечетных чисел от 1 до 100 следующим образом:
- Сначала создайте массив всех чисел от 1 до 50
- Второе удвоение значений массива
- Вычтите 1.
- Сложите значения
1. Создайте массив от 1 до 50
Формула СТРОКА (OFFSET ($ A $ 1 ,,, 100/2)) может использоваться для создания массива чисел от 1 до 50
В резервной ячейке D4 введите = ROW (OFFSET ($ A $ 1 ,,, 100/2)), затем нажмите F9 не вводите
Excel ответит массивом: = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 23; 24; 25; 26; 27; 28; 29; 30; 31; 32; 33; 34; 35; 36; 37; 38; 39; 40; 41; 42; 43; 44; 45; 46; 47; 48; 49; 50}
Как это работает?
Смещение($ A $ 1 ,,, 100/2) устанавливает диапазон от A1 без смещения строки или столбца, но с высотой 100/2 = 50.
В резервной ячейке D6 введите = OFFSET ($ A $ 1 ,,, 100/2), затем нажмите F9 не вводите
Excel ответит массивом: = {0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0}
Мы видим, что массив содержит 50 нулей (вы можете пересчитать их, чтобы проверить).
Верно.
Но это 50 нулевых строк. Модель ; в отдельных строках массива.
Итак, расширенная формула: = СТРОКА (СМЕЩЕНИЕ ($ A $ 1 ,,, 100/2))
Возвращает строки элементов массива, а не значения массива.
2. Удвойте значения
Формула 2 * СТРОКА (СМЕЩЕНИЕ ($ A $ 1 ,,, 100/2)) используется для удвоения значений массива
В запасной ячейке D8 введите = 2 * ROW (OFFSET ($ A $ 1 ,,, 100/2)), затем нажмите F9 не вводите
Excel ответит массивом: = {2; 4; 6; 8; 10; 12; 14; 16; 18; 20; 22; 24; 26; 28; 30; 32; 34; 36; 38; 40; 42; 44; 46; 48; 50; 52; 54; 56; 58; 60; 62; 64; 66; 68; 70; 72; 74; 76; 78; 80; 82; 84; 86; 88; 90; 92; 94; 96; 98; 100}
3.Вычтем 1
Формула 2 * ROW (OFFSET ($ A $ 1 ,,, 100/2)) -1 используется для вычитания значения a из значений массива
В запасной ячейке D10 введите = 2 * ROW (OFFSET ($ A $ 1 ,,, 100/2)) -1, затем нажмите F9 не вводите
Excel ответит массивом: = {1; 3; 5; 7; 9; 11; 13; 15; 17; 19; 21; 23; 25; 27; 29; 31; 33; 35; 37; 39; 41; 43; 45; 47; 49; 51; 53; 55; 57; 59; 61; 63; 65; 67; 69; 71; 73; 75; 77; 79; 81; 83; 85; 87; 89; 91; 93; 95; 97; 99}
4.
 Сложите значения
Сложите значенияФормула = Sum (2 * ROW (OFFSET ($ A $ 1 ,,, 100/2)) -1) используется для сложения значений массива
В резервной ячейке D12 введите = Sum (2 * ROW (OFFSET ($ A $ 1 ,,, 100/2)) -1), затем нажмите F9 не вводите
Excel ответит значением = 2500 , Ответ.
Формула 2: = СУММ (СТРОКА (1: 100) * МОД (СТРОКА (1: 100), 2))
Вторая формула, которую мы рассмотрим:
= СУММ (СТРОКА (1: 100) * МОД (СТРОКА (1: 100), 2)) Ctrl Shift Enter
Эта формула работает путем создания массива значений от 1 до 100 и последующего умножения этого массива на массив нечетных значений от 1 до 100 и последующего сложения полученного массива.
Начнем с: = СУММ (СТРОКА (1: 100) * МОД (СТРОКА (1: 100), 2))
Обратите внимание, что строка (1: 100) используется в формуле дважды.
В запасной ячейке: D17 введите: = Row (1: 100), затем нажмите F9 не вводите
Excel ответит массивом: = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 23; 24; 25; 26; 27; 28; 29; 30; 31; 32; 33; 34; 35; 36; 37; 38; 39; 40; 41; 42; 43; 44; 45; 46; 47; 48; 49; 50; 51; 52; 53; 54; 55; 56; 57; 58; 59; 60; 61; 62; 63; 64; 65; 66; 67; 68; 69; 70; 71; 72; 73; 74; 75; 76; 77; 78; 79; 80; 81; 82; 83; 84; 85; 86; 87; 88; 89; 90; 91; 92; 93; 94; 95; 96; 97; 98; 99; 100}
Массив значений от 1 до 100.
Далее мы посмотрим на раздел Mod = SUM (ROW (1: 100) * MOD (ROW (1: 100), 2))
В запасной ячейке: D19 введите: = Mod (Row (1: 100), 2), затем нажмите F9 не вводите
Excel ответит массивом: = {1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0; 1; 0}
Mod возвращает остаток после деления первого параметра на второй
Например: Mod (5,2) = 1 5, разделенное на 2 = 2 Остаток 1 .
Итак, в нашем примере Mod (Array, 2) возвращает значение 1 для нечетных значений и 0 для четных значений.
Затем мы умножаем 2 массива вместе: = СУММ (СТРОКА (1: 100) * МОД (СТРОКА (1: 100), 2))
Это то же самое, что:
= {1; 2; 3; 4; 5; …; 97; 98; 99; 100} * {1; 0; 1; 0; 1; …; 1; 0; 1; 0}
В запасной ячейке: D21 введите: = ROW (1: 100) * MOD (ROW (1: 100), 2), затем нажмите F9 не вводите
Excel ответит массивом: = {1; 0; 3; 0; 5; 0; 7; 0; 9; 0; 11; 0; 13; 0; 15; 0; 17; 0; 19; 0; 21; 0; 23; 0; 25; 0; 27; 0; 29; 0; 31; 0; 33; 0; 35; 0; 37; 0; 39; 0; 41; 0; 43; 0; 45; 0; 47; 0; 49; 0; 51; 0; 53; 0; 55; 0; 57; 0; 59; 0; 61; 0; 63; 0; 65; 0; 67; 0; 69; 0; 71; 0; 73; 0; 75; 0; 77; 0; 79; 0; 81; 0; 83; 0; 85; 0; 87; 0; 89; 0; 91; 0; 93; 0; 95; 0; 97; 0; 99; 0}
Наконец, мы можем сложить значения массива: = SUM (ROW (1: 100) * MOD (ROW (1: 100), 2))
В резервной ячейке: D23 введите: = SUM (ROW (1: 100) * MOD (ROW (1: 100), 2)), затем нажмите F9 не вводите
Excel ответит значением = 2500 , Ответ.
Вариант 1:
В приведенной выше формуле = СУММ (СТРОКА (1: 100) * МОД (СТРОКА (1: 100), 2)) мы описали метод оценки значений массива как нечетных или четных с использованием функции Mod.
Excel имеет встроенную функцию для определения, является ли значение нечетным, и это Isodd ()
Мы можем изменить приведенное выше уравнение для использования Isodd () следующим образом
= СУММ (СТРОКА (1: 100) * ISODD (СТРОКА (1: 100)))
Проверить можно в ячейке D28 .
Что, если я хочу суммировать четные числа?
Мы можем использовать описанный выше вариант, чтобы быстро сложить четные числа от 1 до 100
= СУММ (СТРОКА (1: 100) * ЕЩЕ РАЗ (СТРОКА (1: 100)))
В резервной ячейке: D21 введите: = SUM (ROW (1: 100) * ISEVEN (ROW (1: 100))), затем нажмите F9 не вводите
Excel ответит значением = 2550 , Ответ.
Как еще можно решить
проблему Суниты?Можете ли вы решить проблему Суниты по-другому?
Дайте нам знать в комментариях ниже:
Скачать
Вы можете загрузить копию вышеуказанного файла и следовать по ссылке Скачать здесь.
Формула судебной экспертизы «Серия»
Это 22 и публикаций в серии Formula Forensics.
Вы можете узнать больше о том, как разделить формулы Excel, в следующих сообщениях
Серия Formula Forensic
Formula Forensics нуждается в вашей помощи
Мне нужно больше идей для будущих публикаций Formula Forensics, поэтому мне нужна ваша помощь.
Если у вас есть аккуратная формула, которой вы хотите поделиться и объяснить, попробуйте положить ручку на бумагу и набросать сообщение, как указано выше, или;
Если у вас есть формула, которую вы хотели бы объяснить, но не хотите писать пост, отправьте ее Хуи или Чанду.
Статьи по Теме:
Суммирование Рамануджана: 1 + 2 + 3 + ⋯ + ∞ = -1/12? | Марк Доддс | Cantor’s Paradise
«О чем ты, черт возьми, говоришь? Это не может быть правдой! » — Моя мама
Это то, что моя мама сказала мне, когда я рассказал ей об этой маленькой математической аномалии. И это просто аномалия. В конце концов, это противоречит базовой логике. Как может сложение положительных чисел равняться не только отрицательной, но и отрицательной дроби? Что за гидроразрыв?
И это просто аномалия. В конце концов, это противоречит базовой логике. Как может сложение положительных чисел равняться не только отрицательной, но и отрицательной дроби? Что за гидроразрыв?
Прежде чем я начну : Мне было указано, что когда я говорю о суммах в этой статье, это не в традиционном смысле этого слова. Это связано с тем, что все серии, с которыми я имею дело, естественно, не стремятся к определенному числу, поэтому мы говорим о другом типе сумм, а именно о суммировании Чезаро. Для всех, кто интересуется математикой, суммирование Чезаро присваивает значения некоторым бесконечным суммам, которые не сходятся в обычном смысле.«Сумма Чезаро определяется как предел, поскольку n стремится к бесконечности, последовательности средних арифметических первых n частичных сумм ряда» — Википедия. Я также хочу сказать, что на протяжении всей этой статьи я имею дело с концепцией счетной бесконечности, другого типа бесконечности, который имеет дело с бесконечным набором чисел, но такой, в котором, если дать достаточно времени, вы можете сосчитать до любого числа в наборе. Это позволяет мне использовать некоторые из обычных свойств математики, такие как коммутативность в моих уравнениях (это аксиома, которую я использую на протяжении всей статьи).
Это позволяет мне использовать некоторые из обычных свойств математики, такие как коммутативность в моих уравнениях (это аксиома, которую я использую на протяжении всей статьи).
Для тех из вас, кто не знаком с этой серией, которая стала известна как суммирование Рамануджана в честь известного индийского математика Шриниваса Рамануджана, в ней говорится, что если вы сложите все натуральные числа, то есть 1, 2, 3, 4 и так далее, вплоть до бесконечности, вы обнаружите, что оно равно -1/12. Ага, -0.08333333333.
Не верите? Продолжайте читать, чтобы узнать, как я это докажу, доказав два одинаково безумных утверждения:
- 1–1 + 1–1 + 1–1 ⋯ = 1/2
- 1–2 + 3–4 + 5–6 ⋯ = 1/4
Прежде всего, хлеб с маслом.Здесь и происходит настоящее волшебство, ведь два других доказательства без этого невозможны.
Я начинаю с серии A, которая равна 1–1 + 1–1 + 1–1, повторяющейся бесконечное количество раз.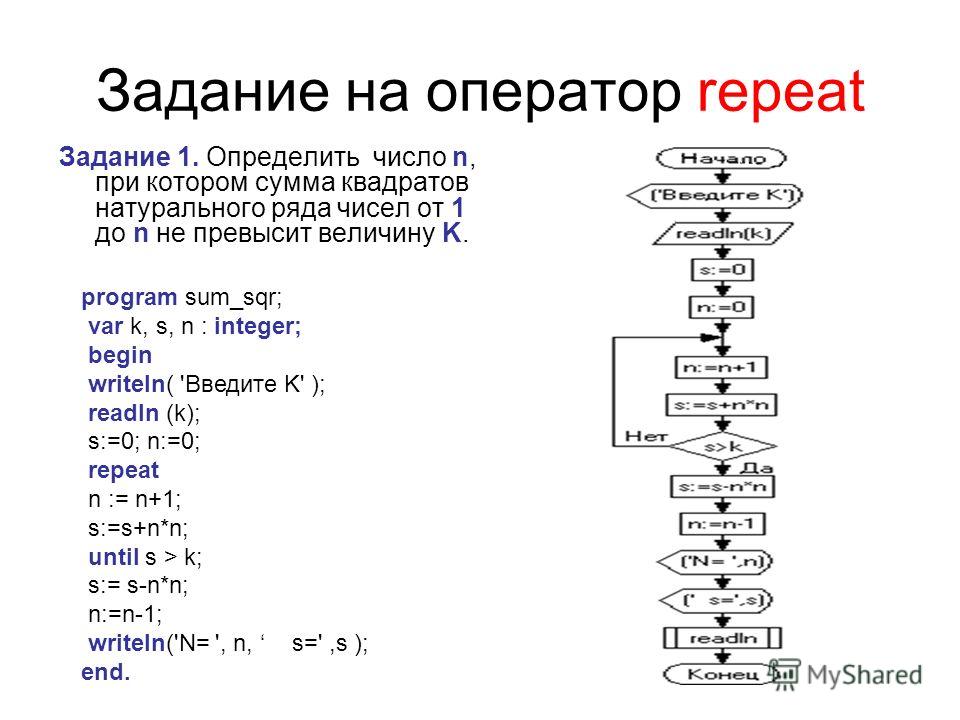 Я напишу это так:
Я напишу это так:
A = 1–1 + 1–1 + 1–1 ⋯
Затем я проделаю небольшой хитрый трюк. Я забираю A у 1
1-A = 1- (1–1 + 1–1 + 1–1 ⋯)
Пока все хорошо? Вот где происходит волшебство. Если я упросту правую часть уравнения, я получу кое-что очень необычное:
1-A = 1–1 + 1–1 + 1–1 + 1 ⋯
Знакомо? Если вы его пропустили, это A .Да, в правой части уравнения находится серия, с которой мы начали. Так что я могу заменить эту правую часть на , немного по школьной алгебре и бум!
1-A = A
1-A + A = A + A
1 = 2A
1/2 = A
Эта маленькая красавица серии Гранди, называется такой после итальянского математика, философа и священника Гвидо Гранди. Это действительно все, что есть в этой серии, и, хотя это мой личный фаворит, за этим нет крутой истории или истории открытий. Однако открывает дверь для доказательства множества интересных вещей, включая очень важное уравнение для квантовой механики и даже теории струн. Но об этом позже. А пока мы переходим к доказательству # 2: 1–2 + 3–4 + 5–6 ⋯ = 1/4 .
Однако открывает дверь для доказательства множества интересных вещей, включая очень важное уравнение для квантовой механики и даже теории струн. Но об этом позже. А пока мы переходим к доказательству # 2: 1–2 + 3–4 + 5–6 ⋯ = 1/4 .
Начнем так же, как и выше, положив ряду B = 1–2 + 3–4 + 5–6 ⋯. Затем мы можем начать с этим поиграть. На этот раз вместо того, чтобы вычитать B из 1, мы собираемся вычесть его из A . Математически получим:
AB = (1–1 + 1–1 + 1–1 ⋯) — (1–2 + 3–4 + 5–6 ⋯)
AB = (1– 1 + 1–1 + 1–1 ⋯ ) — 1 + 2–3 + 4–5 + 6 ⋯
Затем мы немного перемешиваем термины и видим, что возникает еще одна интересная закономерность.
AB = (1–1) + (–1 + 2) + (1–3) + (–1 + 4) + (1–5) + (–1 + 6) ⋯
AB = 0 + 1–2 + 3–4 + 5 ⋯
И снова мы получаем ряд, с которого начали, и, как уже говорилось ранее, мы знаем, что A = 1/2 , поэтому мы используем более базовую алгебру и Докажите наш второй потрясающий факт сегодняшнего дня.
A-B = B
A = 2B
1/2 = 2B
1/4 = B
И вуаля! У этого уравнения нет причудливого названия, поскольку оно доказано многими математиками на протяжении многих лет, одновременно называя его парадоксальным уравнением.Тем не менее, это вызвало споры среди ученых в то время и даже помогло расширить исследования Эйлера по проблеме Базеля и привести к важным математическим функциям, таким как дзета-функция Римана.
А теперь глазурь на торте, которую вы так долго ждали, — большой сыр. Мы снова начнем с того, что положим ряду C = 1 + 2 + 3 + 4 + 5 + 6 ⋯, и вы, возможно, догадались это, мы собираемся вычесть C из B .
BC = (1–2 + 3–4 + 5–6 ⋯) — (1 + 2 + 3 + 4 + 5 + 6 ⋯)
Поскольку математика по-прежнему прекрасна, мы собираемся изменить порядок порядок некоторых чисел здесь, чтобы мы получили что-то знакомое, но, вероятно, не то, о чем вы подозреваете.
до н.э. = (1-2 + 3-4 + 5-6 ⋯) -1-2-3-4-5-6 ⋯
до н.э. = (1-1) + (-2-2 ) + (3-3) + (-4-4) + (5-5) + (-6-6) ⋯
BC = 0-4 + 0-8 + 0-12 ⋯
BC = -4-8-12 ⋯
Не то, что вы ожидали, верно? Держись за носки, потому что у меня в рукаве есть последняя хитрость, которая того стоит. Если вы заметили, все члены справа кратны -4, поэтому мы можем извлечь этот постоянный множитель и вот, вот, мы получили то, с чего начали.
BC = -4 (1 + 2 + 3) ⋯
BC = -4C
B = -3C
И так как у нас есть значение для B = 1/4 , мы просто помещаем это значение и получаем волшебный результат:
1/4 = -3C
1 / -12 = C или C = -1/12
Теперь, почему это важно. Во-первых, это используется в теории струн. К сожалению, не в версии Стивена Хокинга, а в первоначальной версии теории струн (называемой Теорией бозонных струн).К сожалению, теория бозонных струн несколько устарела из-за нынешней области интересов, называемой суперсимметричной теорией струн, но исходная теория все еще используется для понимания суперструн, которые являются неотъемлемыми частями вышеупомянутой обновленной теории струн.
К сожалению, не в версии Стивена Хокинга, а в первоначальной версии теории струн (называемой Теорией бозонных струн).К сожалению, теория бозонных струн несколько устарела из-за нынешней области интересов, называемой суперсимметричной теорией струн, но исходная теория все еще используется для понимания суперструн, которые являются неотъемлемыми частями вышеупомянутой обновленной теории струн.
Суммирование Рамануджана также имело большое влияние в области общей физики, в частности, в решении явления, известного как эффект Казимира. Хендрик Казимир предсказал, что, учитывая две незаряженные проводящие пластины, помещенные в вакуум, между этими пластинами существует сила притяжения из-за присутствия виртуальных частиц, хлеба за счет квантовых флуктуаций.В решении Казимира он использует ту самую сумму, которую мы только что доказали, для моделирования количества энергии между пластинами. И вот почему эта ценность так важна.
Итак, у вас есть суммирование Рамануджана, которое было обнаружено в начале 1900-х годов, которое все еще оказывает влияние почти 100 лет спустя во многих различных областях физики, и все еще может выиграть пари у людей, которые не в этом разбираются. .
.
П.С. Если вам все еще интересно и вы хотите узнать больше, вот разговор с двумя физиками, пытающимися объяснить это безумное уравнение и их взгляды на его полезность и значимость.Это красиво, коротко и очень интересно. https://physicstoday.scitation.org/do/10.1063/PT.5.8029/full/
сумма первых n натуральных чисел
Натуральные числа 1,2,3,4, … итак, сумма первых n натуральных чисел числа как1 + 2 + 3 + 4 + … + n
$ S_ {n} $ = 1 + 2 + 3 + 4 + … + n
Как мы знаем,
$ S_ {n} = \ frac {n} {2} [2a + (n-1) d] $
Согласно натуральным числам
первый член = a = 1 и общая разница = d = 1
∴ $ S_ {n} = \ frac {n} {2} [2 \ times 1 + (n-1) \ times1] $
$ S_ {n} = \ frac {n} {2} [2 + n-1] $
$ S_ { n} = \ frac {n} {2} [n + 1] $
Примеры суммы первых n натуральных чисел
1) Найдите сумму первых 20 членов A.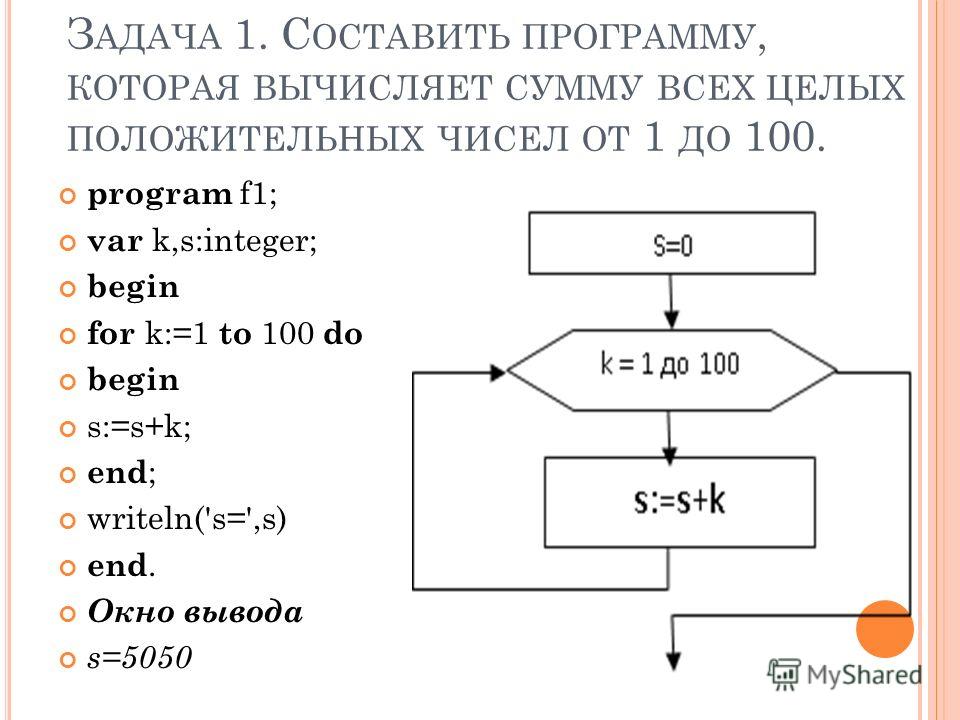 P.
P. Решение: Как мы знаем, чтобы найти сумму первых n натуральных чисел, мы используем следующую формулу:
$ S_ {n} = \ frac {n} {2} [n + 1] $
Поскольку здесь нам нужно найти сумму 20 членов, значит,
n = 20
$ S_ {20} = \ frac {20} {2} [20 + 1] $
$ S_ {20} = 10 \ times $ 21
$ S_ {20} $ = 210
2) Найдите сумму первых 55 членов AP
$ S_ {n} = \ frac {n} {2} [n + 1] $
Поскольку здесь мы должны найти сумму 55 членов, поэтому
n = 55
$ S_ {55} = \ frac {55} {2} [55 + 1]
$ S_ {55} = \ frac {55} {2} \ times 56 $
$ S_ {55} = 28 \ times 55 $
$ S_ {55 } $ = 1540
3) Сумма первых n членов A.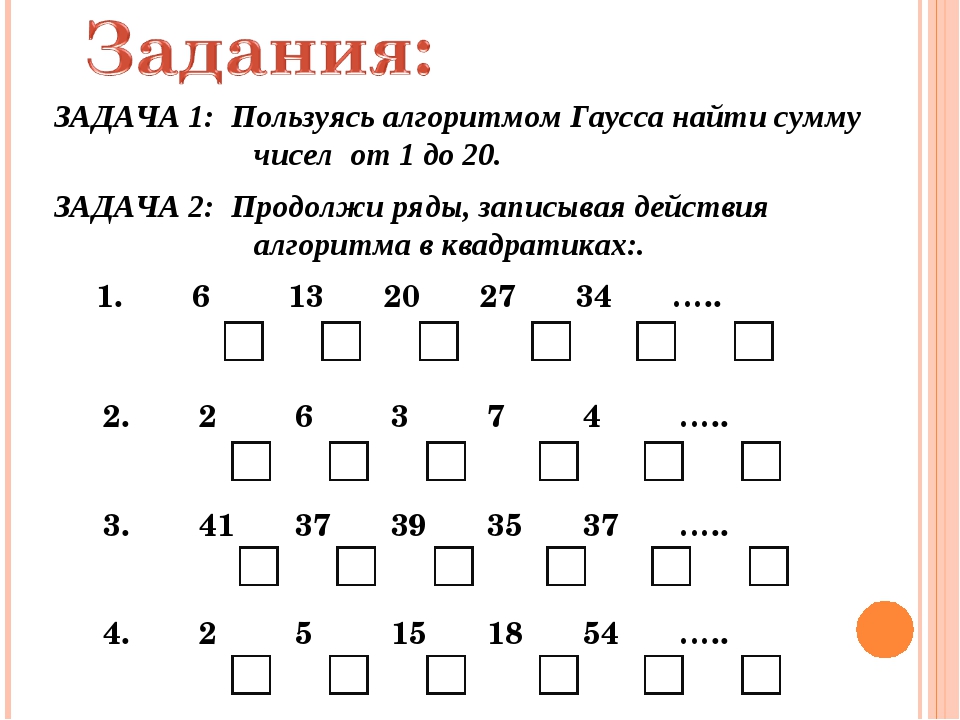 {2} $ + n — 240 = 0
{2} $ + n — 240 = 0
Теперь это квадратное уравнение, поэтому мы найдем множители этого
Факторы:
(n + 16) (n -15) = 0
∴ n = -16 или n = 15
Но количество членов никогда не будет отрицательным, поэтому значение n = 15.
Итак, сумма первых 15 членов AP равна 120.
От суммы первых n натуральных чисел до Home
Covid-19 привел мир к феноменальному переходу.
За электронным обучением будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
Программа GO для вычисления суммы натуральных чисел с использованием цикла for …
Параллелизм — это способность программы выполнять несколько задач одновременно. Это означает, что программа имеет две или более задач, которые выполняются отдельно друг от друга примерно в одно и то же время, но остаются частью одной программы.Параллелизм очень важен в современном программном обеспечении из-за необходимости выполнять независимые фрагменты кода как можно быстрее, не нарушая общий поток программы. Параллелизм в Golang — это способность функций работать независимо друг от друга. Горутина — это функция, которая может работать одновременно с другими функциями. Когда вы создаете функцию как горутину, она рассматривается как независимая единица работы, которая планируется, а затем выполняется на доступном логическом процессоре.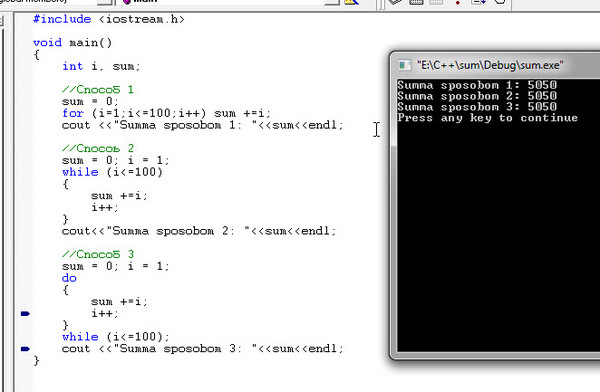 Планировщик времени выполнения Golang имеет функцию управления всеми созданными горутинами, которым требуется процессорное время. Планировщик связывает потоки операционной системы с логическими процессорами для выполнения горутин. Находясь поверх операционной системы, планировщик контролирует все, что связано с тем, какие горутины работают на каких логических процессорах в любой момент времени. Популярные языки программирования, такие как Java и Python, реализуют параллелизм с помощью потоков. Golang имеет встроенные конструкции параллелизма: горутины и каналы.Параллелизм в Golang дешев и прост. Горутины — это дешевые, легкие нити. Каналы — это каналы, по которым осуществляется связь между горутинами. Последовательные процессы связи, или сокращенно CSP, используются для описания того, как системы с несколькими параллельными моделями должны взаимодействовать друг с другом. Обычно он в значительной степени полагается на использование каналов в качестве среды для передачи сообщений между двумя или более параллельными процессами и является основной мантрой Golang.
Планировщик времени выполнения Golang имеет функцию управления всеми созданными горутинами, которым требуется процессорное время. Планировщик связывает потоки операционной системы с логическими процессорами для выполнения горутин. Находясь поверх операционной системы, планировщик контролирует все, что связано с тем, какие горутины работают на каких логических процессорах в любой момент времени. Популярные языки программирования, такие как Java и Python, реализуют параллелизм с помощью потоков. Golang имеет встроенные конструкции параллелизма: горутины и каналы.Параллелизм в Golang дешев и прост. Горутины — это дешевые, легкие нити. Каналы — это каналы, по которым осуществляется связь между горутинами. Последовательные процессы связи, или сокращенно CSP, используются для описания того, как системы с несколькими параллельными моделями должны взаимодействовать друг с другом. Обычно он в значительной степени полагается на использование каналов в качестве среды для передачи сообщений между двумя или более параллельными процессами и является основной мантрой Golang. Горутины — горутина — это функция, которая выполняется независимо от функции, которая ее запустила.Каналы — канал — это конвейер для отправки и получения данных. Каналы предоставляют способ для одной горутины отправлять структурированные данные другой. Параллелизм и параллелизм проявляются в картине, когда вы исследуете многозадачность, и они часто используются взаимозаменяемо, параллельный и параллельный относятся к связанным, но различным вещам. справляться с множеством задач одновременно. Это означает, что вы работаете над управлением множеством задач, выполняемых одновременно за определенный период времени.Однако вы будете выполнять только одну задачу за раз. Это обычно происходит в программах, где одна задача ожидает, а программа решает запустить другую задачу во время простоя. Это аспект предметной области, когда вашей программе необходимо обрабатывать множество одновременных событий. Параллелизм. Параллелизм заключается в выполнении множества задач одновременно. Это означает, что даже если у нас есть две задачи, они работают непрерывно, без перерывов между ними.
Горутины — горутина — это функция, которая выполняется независимо от функции, которая ее запустила.Каналы — канал — это конвейер для отправки и получения данных. Каналы предоставляют способ для одной горутины отправлять структурированные данные другой. Параллелизм и параллелизм проявляются в картине, когда вы исследуете многозадачность, и они часто используются взаимозаменяемо, параллельный и параллельный относятся к связанным, но различным вещам. справляться с множеством задач одновременно. Это означает, что вы работаете над управлением множеством задач, выполняемых одновременно за определенный период времени.Однако вы будете выполнять только одну задачу за раз. Это обычно происходит в программах, где одна задача ожидает, а программа решает запустить другую задачу во время простоя. Это аспект предметной области, когда вашей программе необходимо обрабатывать множество одновременных событий. Параллелизм. Параллелизм заключается в выполнении множества задач одновременно. Это означает, что даже если у нас есть две задачи, они работают непрерывно, без перерывов между ними.

 Задача гениального Гаусса (2
часа)
Задача гениального Гаусса (2
часа)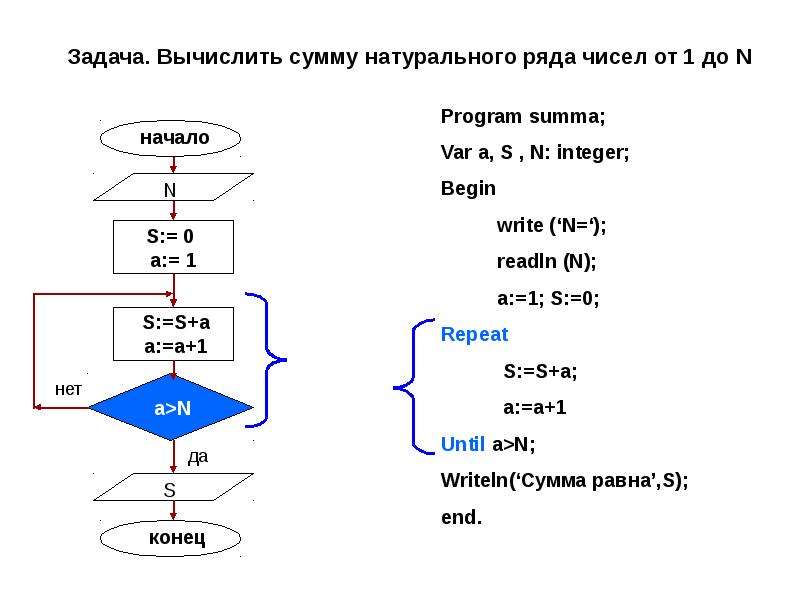 Вы сегодня
узнаете кто такой Гаусс и
что такое метод Гаусса и
как его можно применить.
Вы сегодня
узнаете кто такой Гаусс и
что такое метод Гаусса и
как его можно применить.
 Как же
маленькому Гауссу
удалось быстро
подсчитать сумму?
Запишите в тетради: Карл
Гаусс, 18в, Германия.
Чтобы понять, как
рассуждал Гаусс,
разберем задачу
Как же
маленькому Гауссу
удалось быстро
подсчитать сумму?
Запишите в тетради: Карл
Гаусс, 18в, Германия.
Чтобы понять, как
рассуждал Гаусс,
разберем задачу
 При этом надо дать
возможность каждому
получить за это задание
по 1 баллу, т.е. если у кого-то
будет неверно подправить
его или подсказать. Затем
вызывает к доске трех
желающих и спрашивает
как они нашли ответ. При
этом учащиеся учатся
проговаривать свое
решение. То есть они
показывают словесно
другим учащимся как они
рассуждали. Если все
ответы одинаковые, стоит
послушать каждого.
При этом надо дать
возможность каждому
получить за это задание
по 1 баллу, т.е. если у кого-то
будет неверно подправить
его или подсказать. Затем
вызывает к доске трех
желающих и спрашивает
как они нашли ответ. При
этом учащиеся учатся
проговаривать свое
решение. То есть они
показывают словесно
другим учащимся как они
рассуждали. Если все
ответы одинаковые, стоит
послушать каждого. Бывает очень интересно.
После этого необходимо
перейти к важному шагу. А
как же считал Гаусс. Как
по другому можно найти
ответ. Мы для этого на
доске делаем маленькую
подсказку и при этом
будем молчать(соединяем
линией числа в пары 1 с10, 2
с 9,…,5 с 6). 1+2+3+4+5+6+7+8+9+10.
Хотя некоторые из ребят
покажут и расскажут
правильное другое
решение и получат за это 1
балл, учителю надо
показать самим как
решается задача, чтобы у
детей был более точный
образец рассуждения.
Бывает очень интересно.
После этого необходимо
перейти к важному шагу. А
как же считал Гаусс. Как
по другому можно найти
ответ. Мы для этого на
доске делаем маленькую
подсказку и при этом
будем молчать(соединяем
линией числа в пары 1 с10, 2
с 9,…,5 с 6). 1+2+3+4+5+6+7+8+9+10.
Хотя некоторые из ребят
покажут и расскажут
правильное другое
решение и получат за это 1
балл, учителю надо
показать самим как
решается задача, чтобы у
детей был более точный
образец рассуждения. Объединим слагаемые в
пары – первое с десятым,
второе с девятым и т.д.
Всего у нас 5 таких пар, и
каждая пара в сумме дает
11. Поэтому искомая сумма
равна 11 × 5 = 55.
Объединим слагаемые в
пары – первое с десятым,
второе с девятым и т.д.
Всего у нас 5 таких пар, и
каждая пара в сумме дает
11. Поэтому искомая сумма
равна 11 × 5 = 55.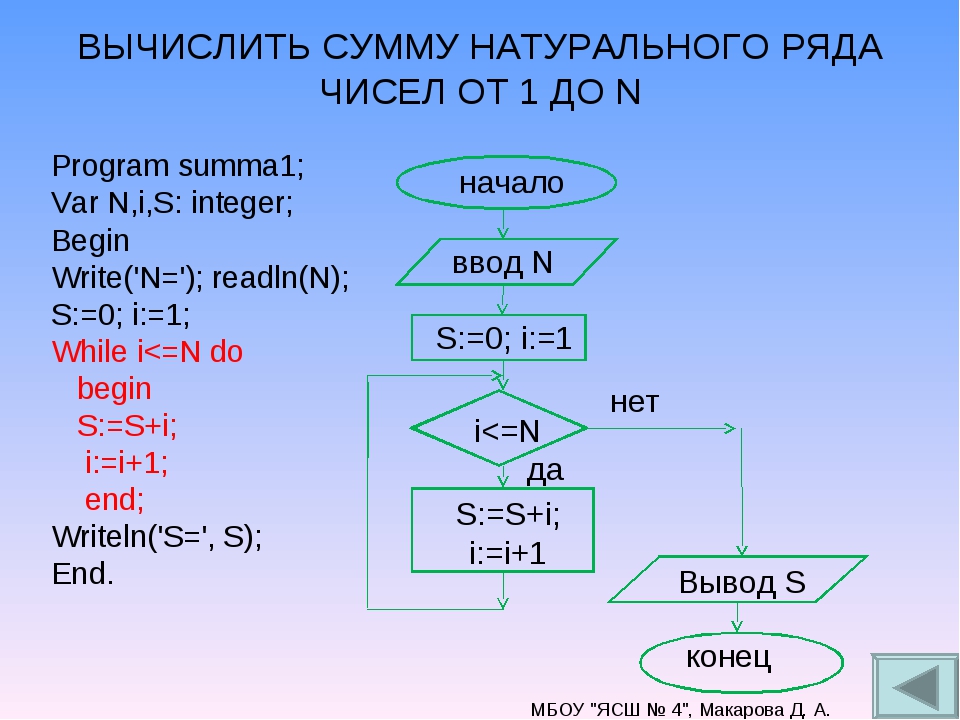 Ответ: (1+14)× 7=105. За
правильное решение 1 балл.
Здесь и в дальнейшем за
правильные идеи и
решения надо
стимулировать учащихся,
т.к. на олимпиадах даже за
неполное решение, а за
правильный подход ученик
может получить
дополнительные баллы. И к
этому мы приучаем уже на
наших занятиях.
Ответ: (1+14)× 7=105. За
правильное решение 1 балл.
Здесь и в дальнейшем за
правильные идеи и
решения надо
стимулировать учащихся,
т.к. на олимпиадах даже за
неполное решение, а за
правильный подход ученик
может получить
дополнительные баллы. И к
этому мы приучаем уже на
наших занятиях.
 Эта задача
потруднее, т.к. все числа
уже нельзя разбить на
пары. Попросить ребят все
же воспользоваться
разбиением на пары тех
чисел, с которыми это
можно сделать. Ответ: (1+9)×
4+9=45, 55-10=45. Данный
результат также будет
часто встречаться в
олимпиадных задачах.
Эта задача
потруднее, т.к. все числа
уже нельзя разбить на
пары. Попросить ребят все
же воспользоваться
разбиением на пары тех
чисел, с которыми это
можно сделать. Ответ: (1+9)×
4+9=45, 55-10=45. Данный
результат также будет
часто встречаться в
олимпиадных задачах.
 Здесь
учителю можно дать время
решить детям самим, а
затем после совместного
обсуждения записать
решение у доски. Найти
сумму чисел от 1 до 100.
Трудность заключается в
форме записи 1+2+3…+98+99+100.
Надо объяснить, что все
числа мы не можем
записать, поэтому
используем такую запись:
1+2+3+…+98+99+100=(1+100)× 50.
Ответ: (1+100)× 50=5050.
Здесь
учителю можно дать время
решить детям самим, а
затем после совместного
обсуждения записать
решение у доски. Найти
сумму чисел от 1 до 100.
Трудность заключается в
форме записи 1+2+3…+98+99+100.
Надо объяснить, что все
числа мы не можем
записать, поэтому
используем такую запись:
1+2+3+…+98+99+100=(1+100)× 50.
Ответ: (1+100)× 50=5050.
 Имеется 9 гирь
весом 1г, 2г, 3г, 4г, 5г, 6г, 7г,
8г, 9г. Можно ли разложить
на три кучки равным весом?
Решение. Сумма масс всех
гирек 45г. Значит в одной
кучке будут гири весом 15г.
Попробуем это сделать: 1г+9г+5г,2г+6г+7г,3г+4г+8г.
Здесь возможны и другие
результаты, например: 1г+8г+6г,
3г+5г+7г, 2г+4г+9г.
Имеется 9 гирь
весом 1г, 2г, 3г, 4г, 5г, 6г, 7г,
8г, 9г. Можно ли разложить
на три кучки равным весом?
Решение. Сумма масс всех
гирек 45г. Значит в одной
кучке будут гири весом 15г.
Попробуем это сделать: 1г+9г+5г,2г+6г+7г,3г+4г+8г.
Здесь возможны и другие
результаты, например: 1г+8г+6г,
3г+5г+7г, 2г+4г+9г.

 Впереди одна птица(вожак),
за ней две, потом три,
четыре и т.д. Сколько птиц
в стае, если в последнем
ряду их 20? Ответ: Это
сумма чисел от 1 до 20. (1+20)×10=210.
Впереди одна птица(вожак),
за ней две, потом три,
четыре и т.д. Сколько птиц
в стае, если в последнем
ряду их 20? Ответ: Это
сумма чисел от 1 до 20. (1+20)×10=210.


 Ее
третья часть – 78:3=26.
Разобьем все гири на пары
1-12, 2-11, 3-10, 4-9, 5-8, 6-7. Если мы
уберем 4 гири весом 26
грамм, то при этом мы «разобьем»
самое большее четыре
пары, а две пары
останутся точно
нетронутыми, которые
составляют тоже треть
общей массы. Таким
образом. Мы получили
первую четверку убранную,
вторую четверку
гарантированно
оставшуюся (две пары) и
третью четверку
нетронутую, которая тоже
будет весом 26 грамм.
Ее
третья часть – 78:3=26.
Разобьем все гири на пары
1-12, 2-11, 3-10, 4-9, 5-8, 6-7. Если мы
уберем 4 гири весом 26
грамм, то при этом мы «разобьем»
самое большее четыре
пары, а две пары
останутся точно
нетронутыми, которые
составляют тоже треть
общей массы. Таким
образом. Мы получили
первую четверку убранную,
вторую четверку
гарантированно
оставшуюся (две пары) и
третью четверку
нетронутую, которая тоже
будет весом 26 грамм.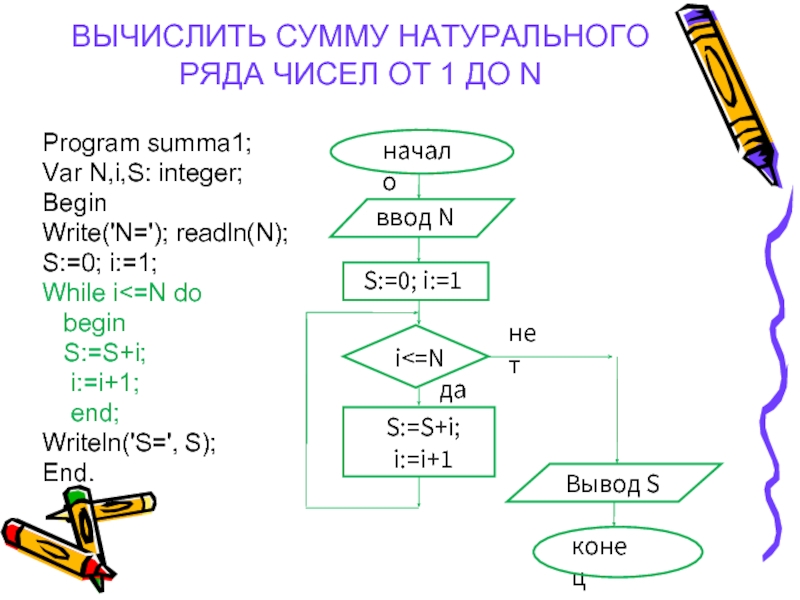 Ответ: Можно.
Ответ: Можно.
Leave a Reply