Как выучить алгебру с нуля самостоятельно: Как быстро и легко выучить алгебру: советы для школьников

Как быстро и легко выучить алгебру: советы для школьников

В статье мы расскажем о платных и бесплатных способах быстро выучить алгебру. Разберемся, как запомнить правила, теоремы и функции, какие темы можно освоить за лето, месяц или неделю и как получать хорошие оценки на уроках.

Если у вас нет больших пробелов в знании школьной программы, то можно заниматься алгеброй самостоятельно. В интернете вы можете бесплатно скачать разные учебные материалы: электронные учебники, рабочие тетради, схемы, задачники, онлайн-тесты и пр.

Самообучение – это самый доступный способ подготовки, так как не нужно оплачивать услуги репетитора, согласовывать время, подстраиваться под расписание преподавателя и т. д. Но выучить алгебру с нуля самому будет сложно, особенно если вы учитесь в 8-9 классе, когда большая часть материала уже пройдена.

Минусы самостоятельного обучения:

• Трудно придерживаться графика. Дополнительные занятия сложно совмещать с уроками в школе, спортивными секциями и кружками, а гаджеты, видеоигры или встречи с друзьями сильно отвлекают от учебы.
• Некому проверить домашнее задание и ответить на вопросы. Придется искать ответы в интернете, тратить время на поиски, читать форумы, проверять достоверность информации и т. д.
• Тяжело самому разобраться со сложными темами. Можно заучить формулы и пользоваться ими для решения типовых задач. Но вряд ли вы научитесь самостоятельно решать задания повышенной сложности.

Самый удобный, эффективный и легкий способ выучить алгебру – это дистанционное обучение в онлайн-школе: на индивидуальных уроках с репетитором или на курсах. Расскажем подробнее про оба варианта.

Заниматься с репетитором можно не только лично, но и онлайн. Стоимость часа в этом случае будет ниже, а качество учебного процесса останется высоким. Уроки проходят по видеосвязи: учитель объясняет новую тему, показывает примеры, отвечает на вопросы, проверяет задания, указывает на ошибки и т. д. Для письменных работ есть интерактивная доска: на ней могут писать и ученик, и преподаватель.

На нашем сайте есть разные сервисы для онлайн-уроков с репетитором. Вы сможете выбрать программу по цене, сравнить условия и почитать отзывы.

Еще один способ учиться дистанционно – это онлайн-курсы с готовой программой:

• На занятиях подробно объясняют все темы из элементарной и линейной алгебры, разбирают примеры.
• Если вы не понимаете материал, то можете задать вопрос преподавателю по ходу урока или написать куратору в чат в любое время.
• Можно заниматься по удобному графику: смотреть урок онлайн или в записи.
• Такой формат удобно совмещать со школой и кружками.
• Для занятий нужен ПК, ноутбук или планшет.
• В личном кабинете вы можете посмотреть видео, почитать конспекты или пособие и сделать домашнее задание – доступ к учебным материалам останется навсегда.

В детском разделе нашего сайта собраны лучшие курсы по алгебре от проверенных онлайн-школ. Вы можете выбрать программу по стоимости, сроку, формату (онлайн или видеокурс), уровню подготовки (базовый, углубленный) и другим параметрам , а также почитать отзывы учеников и их родителей.

Для вашего удобства мы разбили курсы по классам:

• Курсы по алгебре для 7 класса.
• Курсы по алгебре для 8 класса.
• Курсы по алгебре для 9 класса.
• Курсы по алгебре для 10 класса.
• Курсы по алгебре для 11 класса.

Подборка курсов Онлайн-курсы по математике (алгебре и геометрии) 7 класса в 2022 году

Посмотреть подборку

Наши рекомендации для тех, кто хочет выучить все темы по алгебре:

• Составьте программу подготовки. Определите цель (подтянуть знания, подготовиться к экзамену), напишите чек-лист с перечнем тем, которые вы будете изучать, выберите учебные материалы (книги, рабочие тетради, сборники задач и пр.). Строго придерживайтесь плана и занимайтесь регулярно, например, 1-2 раза в неделю.
• Ведите конспекты по каждому параграфу, так как при письме информация запоминается лучше. Например, чтобы быстро выучить формулы сокращенного умножения, можно вручную сделать таблицу, а затем распечатать ее и повесить над рабочим столом.
• Разбирайте задания на примерах. Если вы учитесь в онлайн-школе, то преподаватель покажет разные способы решения задач. Если вы занимаетесь самостоятельно, пользуйтесь задачниками с готовыми ответами, смотрите видеоразборы на Youtube или просите помощь у одноклассников.

Ниже расскажем подробнее о том, как выучить алгебру за короткий срок.

За лето

Если хотите подтянуть алгебру за лето, то занимайтесь на онлайн-курсах. Не придется подстраиваться под жесткий график, но вы сможете выделить 1-2 часа в неделю для видеоуроков. С помощью курсов вы повторите все темы прошедшего учебного года или изучите новый материал.

Подходящие программы есть, к примеру, в онлайн-школе «Фоксфорд»:

• Базовые курсы для 7, 8, 9, 10, 11 классов – около 30 уроков в записи с домашними заданиями. Если вы будете смотреть по 2-3 урока в неделю, то пройдете весь онлайн-курс за время летних каникул.
• Интенсив по математике – 4 видеоурока, на которых повторяют школьную программу по каждому классу.
• Мини-курс «Векторный метод в пространстве» для 10-11 классов, на котором рассказывают про базовые операции над векторами, скалярное или векторное произведение. Состоит из 4 видеолекций.

За месяц

За 4-5 недель вы не успеете подготовиться к экзамену, но сможете повторить пройденный материал, чтобы сдать годовую контрольную. А также этого времени хватит, чтобы закрыть пробелы в знаниях.

3 совета, как выучить алгебру за месяц:

• Сначала изучите теорию и только после этого переходите к практике. Разберитесь с терминами и определениями, посмотрите примеры решений. Если вы часто допускаете ошибки при расчетах, значит, не понимаете тему. Еще раз перечитайте страницы учебника.
• Занимайтесь ежедневно – достаточно 30-40 минут на то, чтобы решить пару задач. Лучше тренироваться регулярно, а не сидеть над книгами по 3-4 часа лишь раз в неделю.
• Не стесняйтесь задавать вопросы. Если вы не поняли какую-то тему, то можете обратиться за помощью к родителям, одноклассникам, школьному учителю или репетитору.

За неделю

За неделю вы успеете повторить все темы, которые изучали в течение четверти или полугодия. Рекомендации от преподавателей — что можно сделать за 5-7 дней:

• Составьте список всех пройденных тем и выполните упражнения по каждой. Затем нужно сравнить свое решение с правильным ответом, после чего сделать упор на те задачи, с которыми справляетесь хуже всего.
• Не зазубривайте материал, а запоминайте теоремы или формулы на конкретных примерах. Вам необходимо освоить хотя бы основные алгоритмы.
• Делайте перерывы в учебе. Многие школьники откладывают подготовку на последний момент, а затем сидят над учебниками по несколько часов ежедневно. Лучше оптимально распределить нагрузку и чередовать алгебру с другими занятиями.

Реально ли подтянуть знания в более короткие сроки

Если вы хотите подтянуть знания по алгебре, чтобы написать контрольную или сдать ЕГЭ, то начинайте подготовку заранее. Накануне ответственного события вы можете выделить 2-3 часа на то, чтобы повторить пройденный материал.

Но изучить новые темы за 1 день вы не успеете. Поэтому не стоит проводить всю ночь над книгами. Лучше как следует выспаться и морально подготовиться. За 5-10 минут до урока можно полистать конспекты по предыдущей теме, а вот перед сдачей экзамена желательно ничего не читать.

Переводите всю новую информацию в наглядную форму – составляйте таблицы, схемы и графики. Важно, чтобы термины, уравнения и функции были собраны в одном месте. Во-первых, так вы лучше их запомните. Во-вторых, вы сможете периодически повторять материал по лекциям.

Чтобы выучить все правила по алгебре, разбирайте их смысл. Не стоит заучивать формулу наизусть – вам нужно понять, что означает каждый элемент, какие задачи можно решать с ее помощью. Для тренировки можно пользоваться двухсторонними карточками. Сделайте с одной стороны описание теоремы, с другой – доказательство.

Чтобы подтянуть оценки по алгебре:

• Проверяйте свои знания сразу после изучения новой темы и спустя некоторое время. Желательно делать это разными способами: с помощью онлайн-тестов, расчетных задач и пр.
• Решайте не только типовые задания из школьных учебников, но и комбинированные, в том числе, повышенного уровня сложности, например, из ЕГЭ или олимпиад.
• Не допускайте пробелов в своих знаниях, своевременно разбирайте ошибки. Если вы не успели хорошо выучить параграф перед уроком, сделайте это после него, но не откладывайте надолго.
• Чаще отвечайте в школе. На занятиях по алгебре у вас будет возможность разобраться со сложными темами с помощью учителя.
• Тренируйтесь считать без калькулятора.
  Это поможет вам развить внимательность и аналитическое мышление.

Что рекомендуют психологи родителям, которые хотят помочь ребенку подтянуть знания по алгебре:

• В большинстве школ алгебра начинается с 7-го класса. Разбирайте вместе сложные темы, проверяйте домашние задания.
• Адекватно оценивайте умственные возможности школьника. Если у вас растет гуманитарий, то без помощи наставника ему будет тяжело освоить точные науки.
• Начинайте подготовку к ОГЭ заранее – в конце 8 или начале 9 класса. Если школьник плохо справляется со школьной программой, то найдите для него репетитора. Заниматься с преподавателем можно онлайн.
• Конец 10 и 11 классы – это самый ответственный период, так как старшекласснику предстоит сдать ЕГЭ, а в некоторых случаях еще и внутренние вступительные испытания в ВУЗ. Чтобы подросток уверенно чувствовал себя на экзамене, запишите его на курсы. В онлайн-школах есть базовые программы по всем школьным предметам и подготовительные онлайн-курсы.

Математика с нуля. Пошаговое изучение математики

«Математика с нуля. Пошаговое изучение математики для начинающих» – это новый проект, предназначенный для людей, которые хотят изучить математику самостоятельно с нуля.

Сразу скажем, здесь нет лёгких решений и подобных заявлений как «Купи эту книгу и сдай математику на 5» или «Освой математику за 12 часов» вы тут не увидите. Математика большая наука, которую следует осваивать последовательно и очень медленно.

Сайт представляет собой уроки по математике, которые упорядочены по принципу «от простого к сложному». Каждый урок затрагивает одну или несколько тем из математики. Уроки разбиты на шаги. Начинать изучение следует с первого шага и далее по возрастанию.

Каждый пройденный урок обязательно должен быть усвоен. Поэтому, не поняв одного урока, нельзя переходить к следующему, поскольку каждый урок в математике основан на понимании предыдущего. Если Вы с первого раза урок не поняли – не расстраивайтесь. Знайте, что некоторые люди потратили месяцы и годы, чтобы понять хотя бы одну единственную тему. Отчаяние и уныние точно не ваш путь. Читайте, изучайте, пробуйте и снова пробуйте.

Математика хорошо усваивается, когда человек самостоятельно открыв учебник, учит самогó себя. При этом вырабатывается определенная дисциплина, которая очень помогает в будущем. Если Вы будете придерживаться принципа «от простого к сложному», то с удивлением обнаружите, что математика не так уж и сложна.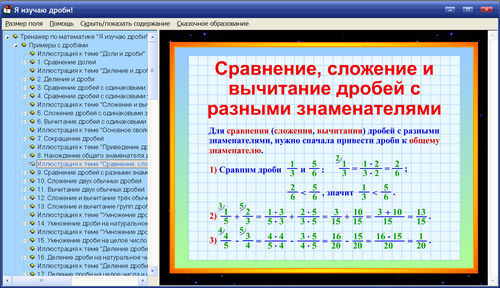 Возможно даже она покажется вам интересной и увлекательной.

Что даст вам знание математики? Во-первых, уверенность. Математику знает не каждый, поэтому осознание того, что вы знаете хоть какую-то часть этой серьёзной науки, делает вас особенным. Во-вторых, освоив математику, вы с лёгкостью освоите другие науки и сможете мыслить гораздо шире. Знание математики позволяет овладеть такими профессиями как программист, бухгалтер, экономист. Никто не станет спорить, что эти профессии сегодня очень востребованы.

В общем, дерзай друг!

Желаем тебе удачи в изучении математики!

• Шаг 1. Числа
• Шаг 2. Основные операции
• Шаг 3. Выражения
• Шаг 4. Замены в выражениях
• Шаг 5. Разряды для начинающих
• Шаг 6. Умножение
• Шаг 7. Деление
• Шаг 8. Порядок действий
• Шаг 9. Законы математики
• Шаг 10. Делители и кратные
• Шаг 11. НОД и НОК
• Шаг 12. Дроби
• Шаг 13. Действия с дробями
• Шаг 14. Смешанные числа
• Шаг 15. Сравнение дробей
• Шаг 16. Единицы измерения
• Шаг 17. Применение дробей
• Шаг 18. Десятичные дроби
• Шаг 19. Действия с десятичными дробями
• Шаг 20. Применение десятичных дробей
• Шаг 21. Округление чисел
• Шаг 22. Периодические дроби
• Шаг 23. Перевод единиц
• Шаг 24. Соотношения
• Шаг 25. Пропорция
• Шаг 26. Расстояние, скорость, время
• Шаг 27. Прямая и обратная пропорциональность
• Шаг 28. Проценты
• Шаг 29. Отрицательные числа
• Шаг 30. Модуль числа
• Шаг 31. Что такое множество?
• Шаг 32. Сложение и вычитание целых чисел
• Шаг 33. Умножение и деление целых чисел
• Шаг 34. Рациональные числа
• Шаг 35. Сравнение рациональных чисел
• Шаг 36. Сложение и вычитание рациональных чисел
• Шаг 37. Умножение и деление рациональных чисел
• Шаг 38. Дополнительные сведения о дробях
• Шаг 39. Буквенные выражения
• Шаг 40. Вынесение общего множителя за скобки
• Шаг 41. Раскрытие скобок
• Шаг 42. Простейшие задачи по математике
• Шаг 43. Задачи на дроби
• Шаг 44. Задачи на проценты
• Шаг 45. Задачи на движение
• Шаг 46. Производительность
• Шаг 47. Элементы статистики
• Шаг 48. Общие сведения об уравнениях
• Шаг 49. Решение задач с помощью уравнений
• Шаг 50. Решение задач с помощью пропорции
• Шаг 51. Системы линейных уравнений
• Шаг 52. Общие сведения о неравенствах
• Шаг 53. Системы линейных неравенств с одной переменной
• Шаг 54. Операции над множествами
• Шаг 55. Степень с натуральным показателем
  
• Шаг 56. Степень с целым показателем
  
• Шаг 57. Периметр, площадь и объём
  
• Шаг 58. Одночлены
  
• Шаг 59. Многочлены
• Шаг 60. Формулы сокращённого умножения
  
• Шаг 61. Разложение многочлена на множители
  
• Шаг 62. Деление многочленов
  
• Шаг 63. Тождественные преобразования многочленов
• Шаг 64. Квадратный корень
• Шаг 65. Алгоритм извлечения квадратного корня
  
• Шаг 66. Квадратное уравнение
• Шаг 67. Квадратное уравнение с чётным вторым коэффициентом
  
• Шаг 68. Теорема Виета
  
• Шаг 69. Разложение квадратного трёхчлена на множители
• Шаг 70. Обобщённое понятие модуля числа
  
• Шаг 71. Уравнение с модулем
• Шаг 72. Решение уравнений с модулем методом интервалов
  
• Шаг 73. Неравенства с модулем
  
• Шаг 74. Решение неравенств с модулем методом интервалов
  
• Шаг 75. Извлечение квадратного корня из обеих частей уравнения
  

Новые уроки будут скоро. Оставайся с нами!

Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Введение в алгебру

Алгебра — это очень весело — ты можешь решать головоломки!

Головоломка

Какой пропущенный номер?

−

2

=

4

Хорошо, ответ 6, верно? Потому что 6 — 2 = 4 . Легкие вещи.

Ну, в алгебре мы не используем пустые клетки, мы используем буква (обычно это x или y, но подойдет любая буква). Так и пишем:

х

−

2

=

4

Это действительно так просто. Буква (в данном случае x) просто означает «мы еще этого не знаем», и ее часто называют неизвестной или переменной .

И когда решаем пишем:

Зачем использовать письмо?

	Потому что:
	легче написать «х», чем рисовать пустые ящики (и легче сказать «х», чем «пустой ящик»).
	если пустых несколько ящики (несколько «неизвестных») мы можем использовать разные буквы для каждого из них.

Так что x просто лучше, чем пустая коробка. Мы не пытаемся сделать слова с ним!

И это не обязательно должно быть x , это может быть y или w … или любая буква или символ, который нам нравится.

Как решить

Алгебра похожа на головоломку, где мы начинаем с чего-то вроде «x − 2 = 4» и хотим закончить с чем-то вроде «x = 6».

Но вместо того, чтобы говорить «, очевидно, x=6″, используйте этот аккуратный пошаговый подход:

• Разработать что удалить чтобы получить «x =…»
• Удалите его с помощью , выполнив противоположное (сложение противоположно вычитанию)
• Сделайте это с с обеих сторон

Вот пример:

Мы хотим, чтобы
удалить
«−2»

Чтобы убрать его, делаем
наоборот , в
этом случае добавляем 2

Делаем это
обе стороны

Что . ..

Решено!

Почему мы добавили 2 к обеим сторонам?

«Держать баланс»…

Баланс

Добавить 2 к левой стороне

Вышел из равновесия!

Добавить 2 на правую сторону Также

Снова баланс

Просто запомните это:

Чтобы сохранить баланс, что мы делаем с одной стороной из «=» мы также должны сделать с другой стороны !

Посмотрите это в действии на анимации баланса алгебры.

Еще одна головоломка

Решите это:

х

+

5

=

12

Нам нужен ответ вроде «x = …»,
, но +5 мешает этому!
Мы можем отменить +5 на −5 (потому что 5−5=0)

Итак, давайте попробуем вычесть 5 из с обеих сторон 😡 + 5 −5 = 12 −5

Небольшая арифметика (5−5 = 0 и 12−5 = 7) принимает вид: x + 0 = 7

Что просто: x = 7

  Решено!

(Быстрая проверка: 7+5=12)

Попробуй себя

Теперь потренируйтесь на этом листе по простой алгебре, а затем проверьте свои ответы. Попробуйте использовать шаги, которые мы показали вам здесь, а не просто гадать!

Попробуйте ответить на вопросы ниже, а затем прочитайте Введение в алгебру. Умножение

 

1725,1726,1727,1728,3135,3136,3137,3138,3850,3851

Как выучить алгебру простыми шагами

Обновлено 28 мая 2019 г.

Автор Lisa Maloney

Алгебра представляет собой первый крупный концептуальный скачок в вашем математическом образовании, поэтому неудивительно, что она часто пугает новых учеников. Но на самом деле в алгебре вам нужно усвоить только две вещи: концепцию переменных и то, как вы можете ими манипулировать. Самый простой способ выучить алгебру — это именно то, как вас проинструктируют ваши учителя: один маленький шаг за раз, с большим количеством повторений, чтобы помочь каждому понятию усвоиться, чтобы вы были готовы к следующему.

TL;DR (слишком длинный; не читал)

Если вы чувствуете разочарование, ободритесь: это естественная, хотя и неприятная часть изучения новых концепций. Не бойтесь задавать вопросы в классе, потому что велика вероятность, что другие ученики задаются тем же вопросом. И всегда пользуйтесь рабочими часами своего инструктора и любыми репетиторскими услугами, предлагаемыми вашей школой или университетом; оба очень помогают.

Введение в алгебру: основы работы с переменными

Самое первое, что вам нужно освоить в алгебре, — это понятие переменной. Переменные — это буквы, которые служат заполнителями для чисел, значение которых вам неизвестно. Так, например, в уравнении 1 + 2 = x , x — это заполнитель для 3, который должен занимать другую часть уравнения. Чаще всего для переменных используются буквы x и y , хотя вы можете использовать любую букву для переменной.

Что можно делать с алгебраическими переменными

С алгебраическими переменными можно делать абсолютно все, что можно делать с числами. Вы можете складывать их, вычитать, умножать, делить, извлекать из них корень, применять экспоненты. . . вы поняли идею.

Но есть одна загвоздка: хотя вы знаете, что 2 ² = 4, нет способа узнать, чему равно x ² , потому что помните, эта переменная представляет неизвестное число. Таким образом, вместо того, чтобы просто решать операции, которые вы применяете к переменным, вы должны полагаться на свои знания свойств этих операций, которые иногда называют законами математики.

Например, если вы видите что-то вроде 3(2 + 4), приложив немного математики, вы увидите, что ответ будет 3(6) или 18. Но если бы вы столкнулись с 3(2 + y), вы бы не могу сказать то же самое – потому что пока y может равняться 4, а также 1, 2, 3, -5, 26, -452 или любому другому числу, которое вы можете придумать.

Таким образом, вы не можете делать предположения о значении и . Но вы можете применить распределительный закон, который говорит вам, что:

3(2 + y) = 6 + 3y или, если следовать соглашению о том, чтобы ставить сначала переменный член, когда это возможно, 3y + 6. Иногда это то, что вам нужно. возьмем с собой задачу по алгебре; в других случаях вам может быть предоставлено достаточно информации о значении y , чтобы «найти переменную», что означает выяснить, какое числовое значение она представляет.

Хитрости для решения алгебраической переменной

Когда вы приступите к своим первым урокам алгебры для начинающих, вы узнаете несколько полезных приемов для решения уравнений с переменными. Самая важная концепция, которую нужно освоить, заключается в том, что, когда вы сталкиваетесь с уравнением, таким как x = 2x + 4 , вы можете делать практически все что угодно с любой частью уравнения — до тех пор, пока вы не забудете сделать то же самое. ко всей другой части уравнения.

Как только вы поймете эту концепцию, вы почти всегда будете следовать простой схеме решения уравнений, включающих переменную:

Сначала выделите переменный член в одной части уравнения.