Как сложить числа от 1 до 100 быстро: Сложите все натуральные числа от 1 до 100
Учитель задал детям вычислить сумму чисел от 1 до 100, пока дети складывали, один ученик решил эту задачу проще. Как он это сделал и кто он был? — Спрашивалка
Андрей Руфов
Учитель задал детям вычислить сумму чисел от 1 до 100, пока дети складывали, один ученик решил эту задачу проще. Как он это сделал и кто он был? задача ребенок число сумма ученик учитель
2763
395
0
Ответы
А.
Ангел .
Немецкий математик Гаусс.Учитель, чтобы занять класс на продолжительное время самостоятельной работой, дал задание ученикам — вычислить сумму всех натуральных чисел от 1 до 100. Маленький Гаусс ответил на вопрос почти мгновенно, чем невероятно удивил всех и, прежде всего, учителя.
Давайте попробуем устно решить задачу о нахождении суммы указанных выше чисел. Для начала возьмём сумму чисел от 1 до 10: 1 +2 + 3 + 4 + 5 + 6 + +7 + 8 + 9 + 10.
Гаусс обнаружил, что 1 + 10 = 11, и 2 + 9 = 11, и так далее. Он определил, что при сложений натуральных чисел от 1 до 10 получается 5 таких пар, и что 5 раз по 11 равно 55.
Гаусс увидел, что сложение чисел всего ряда следует проводить попарно, и составил алгоритм быстрого сложения чисел от 1 до 100.
1 2 3 4 5 6 7 8 …49 50 51 52 …94 95 96 97 98 99 100
1. Необходимо подсчитать количество пар чисел в последовательности от 1 до 100. Получаем 50 пар.
2. Складываем первое и последнее числа всей последовательности. В нашем случае это 1 и 100. Получаем 101.
3. Умножаем количество пар чисел в последовательности на полученную в пункте 2 сумму. Получаем 5050.
Таким образом, сумма натуральных чисел от 1 до 100 равна 5050.
Простая формула: сумма чисел от 1 до n = n * (n+1) : 2.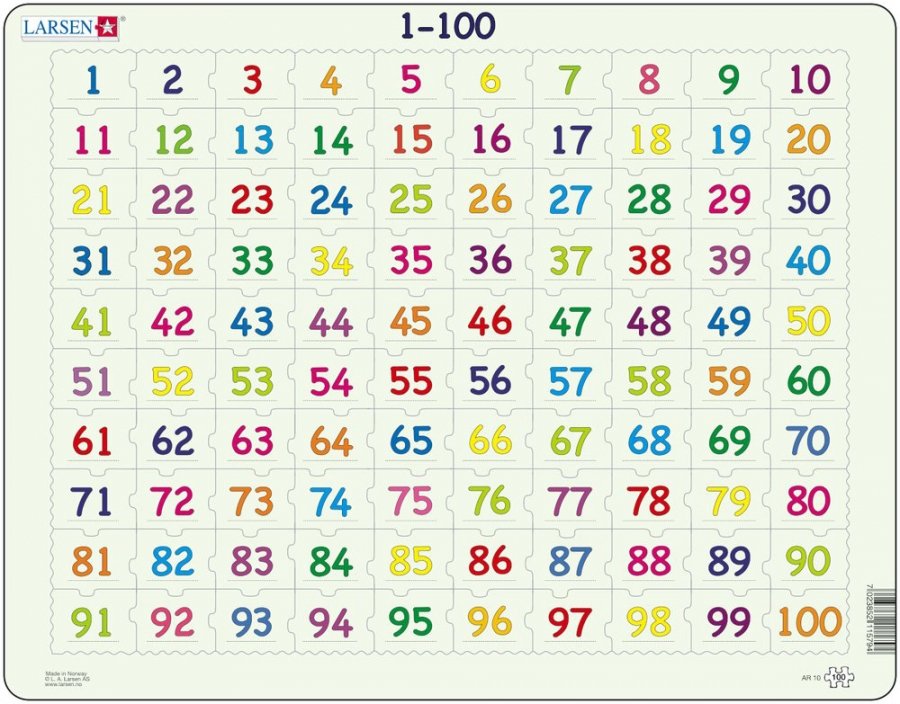
0
Томас Манн
По широко распространённой легенде школьный учитель Карла Фридриха Гаусса, когда последнему было 10 лет, предложил своим ученикам найти сумму всех натуральных чисел от одного до ста. Маленький Карл удивил всех, практически мгновенно предложив правильный ответ. Он заметил, что сумма каждой пары слагаемых, одинаково отстоящих от концов ряда натуральных чисел [1..100], равна 101 (1+100, 2+99, 3+98,…, 50+51). А поскольку число таких пар равно 100/2, то есть 50, он посчитал в уме, что искомая сумма равна 101 × 50 = 5050.
0
Ma
Ma-Ri
По широко распространённой легенде школьный учитель Карла Фридриха Гаусса, когда последнему было 10 лет, предложил своим ученикам найти сумму всех натуральных чисел от одного до ста.
0
Павел Рябов
Гаусс, 1. Необходимо подсчитать количество пар чисел в последовательности от 1 до 100. Получаем 50 пар. 2. Складываем первое и последнее числа всей последовательности. В нашем случае это 1 и 100. Получаем 101. 3. Умножаем количество пар чисел в последовательности на полученную в пункте 2 сумму. Получаем 5050.
0
_ Дюша _
Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100.
Юный Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 50 \times 101=5050.
0
ХТ
Хитсугай Тоуширо
взял написал все числа от 1 до 100, под ними написал от 100 до 1, увидел, что в каждом столбике сумма 101. умножил 101 на 100, получив сумму всех столбиков, в потом поделил пополам, так как ему нужна была сумма только одного ряда, а не двух.
0
Валентина *
Карл Фридрих Гаус,будущий ученый математик ,в 6 лет сделал так:он отобрал 49 пар чисел в сумме образующих 100 Например 45 и 55, 99 и 1 и так далее остались две непарные цифры 100 и 50 и тогда 49 умножил на 100=4900 а потом к 4900+150=5050
0
MJ
Mazarini J.
Надо складывать первое число с последним, второе с предпоследним и т. д. Сумма каждой такой пары чисел равна 101 и повторяется она 50 раз.
Следовательно, сумма всех целых чисел от 1 до 100 будет равна 101 × 50 = 5050.
0
MJ
Mazarini J.
Забыл написать, Гаусс.
1
Андрей Руфов
верно
1
ЛС
Лёха Степанов
ну понятно что это был один из великих математиков. на первый вопрос отвечать лень. а вообще сейчас любой человек более менее знакомый с рядами просто посчитал на калькуляторе сумму от n=1 до 100
0
Юрий Ракутин
Кто-то из великих,нать думать.
0
Юk
Юkka
Сумма арифметической прогрессии S = (A1+An)/2*n = (1+100)/2*100 = 101*100/2 = 5050
Рассуждая чисто логически:
1+..+49 + 50 + 51+..+99 + 100
группируем иначе слагаемые:
(1+99)+(2+98)..+50+100
т.е. 49 раз по 100 и еще 150
Ученик — Гаусс
0
Из
Изнасиловал_Сетру_Такова_Её_Судьба!
он сложил первую и последнюю цифры. потом умножил их на половину от общего числа цифр. то есть умножил на 50 (100/2). получилось выражение 101 умножить на 50. будет 10100 делить на 2 и равно 5050
0
Лидия Фомичева
ученик это был Карл Фридрих Гаусс /великий математик/ он выделил 49 пар чисел, которая в сумме равнялась ста, остались только два непарных числа 50 и 100, следовательно 49х100+50+100= 5050
0
Яр
Ярослав
5050 — за эту задачу мой отец в году «отлично» получил, когда в школе учился.
Сообразил меньше чем за минуту… Логика простая — в ряде чисел от 1 до 100 — 50 пар и само число 50 без пары.
0
Немо
Карл Фридрих Гаусс Он выделил 49 пар чисел: 99 и 1, 98 и 2, 97 и 3 … 51 и 49. В сумме каждая пара чисел равнялась ста, и оставалось два непарных числа 50 и 100. Следовательно, 49х100+50+100=5050.
0
Наталья Беляева
Карл Фридрих Гаусс .Он выделил 49 пар чисел: 99 и 1, 98 и 2, 97 и 3…51 и 49. В сумме каждая пара чисел равнялась ста, и оставалось два непарных числа 50 и 100. Следовательно, 49х100+50+100=5050
0
Bo
Boris
Это был Карл Гаусс.
Только задача была на нахождение суммы всех чисел от 1 до 40. Он сложил первое и последнее число и умножил эту сумму на половинное количество чисел.
0
Еva (Аnna Paula) Braun
Я ЧТО ЭТО ДОЛЖНА ПОМНИТЬ 20 ЛЕТ?…
1
Bo
Boris
А Вы попробуйте посчитать сами. Только не на бумажке.
1
Еva (Аnna Paula) Braun
Я НА РАБОТЕ…И У МЕНЯ ЛЮДИ…))))))))))))))))))))))))))))))))))))))))…МНЕ НАДО ПОСМОТРЕТЬ НА КРТИНУ ВНИМАТЕЛЬНО…ДОМА СДЕЛАЮ..
1
Bo
Boris
Буду ждать ответа.
1
Еva (Аnna Paula) Braun
ОК…
1
Дамир Хасанов
Карл Гаусс, он вывел 49 пар равных 100 и прибавил еще два непарных числа 50 и 100. … Гаусс: сумма чисел от 1 до n = n * (n+1) : 2. Вместо n подставляйте последнее число и вычисляйте.
0
Мира
немецкий ученый Карл Гаусс уже в школьном возрасте смог быстро сложить все числа от 1 до 100, применив простое решение: 101 х 50 = 5050. формула: сумма чисел от 1 до n = n * (n+1) : 2.
0
ЕС
Евгений Стариков
Обычно отвечают: «Эйнштейн».
Реже: «Ландау, Ломоносов, Ньютон, Ковалевская и т.д.» … А это был Иоганн Карл Фридрих Гаусс, немецкий математик и астроном 19 века…
0
Следующая страница
Другие вопросы
куда можно съездить отдохнуть за 300-400 у. е на дней пять-шесть?
Какой процент на данном ресурсе убогих умом?
Помогите, пожалуйста, перевести с английского!! ! Для автопереводчика это слишком сложный случай.
Абонент забыл последнюю цифру номера телефона и поэтому набирает ее наудачу. Найдите вероятность того, что ему придется
Помогите, пожалуйста с русским языком!
помогите пожалуйста решить 3 или 4 задачу
когда подписали договор в Вискулях Ельцин и Шушкевич?
подскажите вот сейчас у нас в городе в связном samsung galaxy note 2 стоит 29000 сколько он будет стоить летом 2013
этанол-ценное вещество его применяют для
На сколько дней дают больничный после биопсии лимфоузла на грудной клетке?
единство вечного и сегодняшнего в романе Булгакова «Мастер и Маргарита»
как перевести на англ.
Очаковское шоссе (нужно для указания адреса)
какой сюрприз придумать или сделать своей девушке за 2 часа
как он лайн узнать результаты теста ielts kz?
Каким должен быть человек, чтобы его захотелось ЗАТРАВИТЬ?
Сумма и произведение цифр числа. Решение задачи на Python
Одной из часто используемых задач для начинающих изучать программирование является нахождение суммы и произведения цифр числа. Число может вводиться с клавиатуры или генерироваться случайное число. Задача формулируется так:
Дано число. Найти сумму и произведение его цифр.
Например, сумма цифр числа 253 равна 10-ти, так как 2 + 5 + 3 = 10. Произведение цифр числа 253 равно 30-ти, так как 2 * 5 * 3 = 30.
Обычно предполагается, что данная задача должна быть решена арифметическим способом. То есть с заданным число должны производиться определенные арифметические действия, позволяющие извлечь из него все цифры, затем сложить их и перемножить.
При этом используются операции деления нацело и нахождения остатка. Если число разделить нацело на 10, произойдет «потеря» последней цифры числа. Например, 253 ÷ 10 = 25 (остаток 3). С другой стороны, эта потерянная цифра есть остаток от деления. Получив эту цифру, мы можем добавить ее к сумме цифр и умножить на нее произведение цифр числа.
Пусть n – само число, suma – сумма его цифр, а mult – произведение. Тогда алгоритм нахождения суммы и произведения цифр можно словесно описать так:
- Переменной suma присвоить ноль.
- Переменной mult присвоить единицу. Присваивать 0 нельзя, так как при умножении на ноль результат будет нулевым.
- Пока значение переменной n больше нуля повторять следующие действия:
- Найти остаток от деления значения n на 10, то есть извлечь последнюю цифру числа.
- Добавить извлеченную цифру к сумме и увеличить на эту цифру произведение.
- Избавиться от последнего разряда числа n путем деления нацело на 10.
В языке Python операция нахождения остатка от деления обозначается знаком процента — %. Деление нацело — двумя слэшами — //.
Код программы на языке Python
n = int(input())
suma = 0
mult = 1
while n > 0:
digit = n % 10
suma = suma + digit
mult = mult * digit
n = n // 10
print("Сумма:", suma)
print("Произведение:", mult)Пример выполнения:
253 Сумма: 10 Произведение: 30
Изменение значений переменных можно записать в сокращенном виде:
...
while n > 0:
digit = n % 10
suma += digit
mult *= digit
n //= 10
...Приведенная выше программа подходит только для нахождения суммы и произведения цифр натуральных чисел, то есть целых чисел больше нуля. Если исходное число может быть любым целым, следует учесть обработку отрицательных чисел и нуля.
Если число отрицательное, это не влияет на сумму его цифр. В таком случае достаточно будет использовать встроенную в Python функции abc, которая возвращает абсолютное значение переданного ей аргумента. Она превратит отрицательное число в положительное, и цикл while с его условием n > 0 будет работать как и прежде.
Если число равно нулю, то по логике вещей сумма его цифр и их произведение должны иметь нулевые значения. Цикл срабатывать не будет. Поскольку исходное значение mult — это 1, следует добавить проверку на случай, если заданное число — это ноль.
Программа, обрабатывающая все целые числа, может начинаться так:
n = abs(int(input()))
suma = 0
mult = 1
if n == 0:
mult = 0
...Заметим, если в самом числе встречается цифра 0 (например, 503), то произведение всех цифр будет равно нулю. Усложним задачу:
Вводится натуральное число. Найти сумму и произведение цифр, из которых состоит это число.
При этом если в числе встречается цифра 0, то ее не надо учитывать при нахождении произведения.Для решения такой задачи в цикл добавляется проверка извлеченной цифры на ее неравенство нулю. Делать это надо до умножения на нее значения переменной-произведения.
n = int(input())
suma = 0
mult = 1
while n > 0:
digit = n % 10
if digit != 0:
suma += digit
mult *= digit
n = n // 10
print("Сумма:", suma)
print("Произведение:", mult)Обратим внимание, что заголовок условного оператора if digit != 0: в Python можно сократить до просто if digit:. Потому что 0 — это False. Все остальные числа считаются истиной.
Приведенный выше математический алгоритм нахождения суммы и произведения цифр числа можно назвать классическим, или универсальным. Подобным способом задачу можно решить на всех императивных языках, независимо от богатства их инструментария. Однако средства языка программирования могут позволить решить задачу другим, зачастую более простым, путем.
Например, в Python можно не преобразовывать введенную строку к числу, а извлекать из нее отдельные символы, которые преобразовывать к целочисленному типу int:
a = input()
suma = 0
mult = 1
for digit in a:
suma += int(digit)
mult *= int(digit)
print("Сумма:", suma)
print("Произведение:", mult)Если добавить в код проверку, что извлеченный символ строки действительно является цифрой, то программа станет более универсальной. С ее помощью можно будет считать не только сумму и произведение цифр целых чисел, но и вещественных, а также цифр, извлекаемых из произвольной строки.
n = input()
suma = 0
mult = 1
for digit in n:
if digit.isdigit():
suma += int(digit)
mult *= int(digit)
print("Сумма:", suma)
print("Произведение:", mult)Пример выполнения:
это3 чи3с9ло! Сумма: 15 Произведение: 81
Строковый метод isdigit проверяет, состоит ли строка только из цифр. В нашем случае роль строки играет одиночный, извлеченный на текущей итерации цикла, символ.
Глубокое знание языка Python позволяет решить задачу более экзотическими способами:
import functools
n = input()
n = [int(digit) for digit in n]
suma = sum(n)
mult = functools.reduce(lambda x, y: x*y, n)
print("Сумма:", suma)
print("Произведение:", mult)Выражение [int(digit) for digit in n] представляет собой генератор списка. Если была введена строка "234", будет получен список чисел: [2, 3, 4].
Встроенная функция sum считает сумму элементов переданного ей аргумента.
Функция reduce модуля functools принимает два аргумента — лямбда-выражение и в данном случае список. Здесь в переменной x происходит накопление произведения, а y принимает каждое следующее значение списка.
Больше задач в PDF
«Быстрый» способ нахождения суммы чисел от $1$ до $100$, которые не делятся на $3$ и $5$
спросил
Изменено 11 лет, 2 месяца назад
Просмотрено 508 раз
$\begingroup$
Найдите сумму чисел от $1$ до $100$, которые не делятся на $3$ и $5$?
Я понимаю, что здесь нам нужно суммировать эти числа:
$1+2+4+7+8+11+13+14+16+17+19+22+23+26+28+29+ 31+32+34$$+37+38+41+43+44+46+47+49+52+53 +56+58+59+61+62+64+67+68+71$ $+73+74+76+77+79+82+83+86+88+89+91+92+94+97+98 $
Что дает сумму $ = 2632 $, но я не соотношу числа в этой серии, есть идеи? Кроме того, я должен сделать это под монетным двором, поэтому, пожалуйста, намекните / ответьте соответственно.
- элементарная теория чисел
$\endgroup$
4
$\begingroup$
Это комбинаторный аргумент, называемый принципом включения-исключения: $$X=1+\ldots+100 — 3(1+\ldots+33) — 5(1+\ldots+20) + 15(1+\ldots+6)$$
Сначала складываем все числа , то мы удаляем все те, которые делятся на $3$, и те, которые делятся на $5$. Но подождите минутку! А 15$? Мы удалили этот номер дважды ! Поэтому нам нужно добавить его один раз, а также остальные его множители ниже $100$.
Теперь с помощью формулы суммирования: $1+\ldots+n = \frac{n(n+1)}{2}$ следует ответ.
$\endgroup$
0
$\begingroup$
Сумма чисел, которые делятся на $3$ в этом диапазоне, равна
$$
3+6+\cdots+99=3(1+2+\cdots+33)
$$
и точно так же сумма делящихся на $5$ равна
$$
5+10+\cdots+100=5(1+2+\cdots+20).
$$
Вы должны знать быструю формулу для сложения этих двух сумм. Будьте осторожны, чтобы сложить все числа, которые делятся на $15$, так как они были вычтены дважды. Благодаря Гауссу мы знаем, что сумма первых $100$ целых чисел составляет $5050$, и после выполнения арифметических действий вы получаете ответ.
$\endgroup$
$\begingroup$
Подсказка: сначала попробуйте найти сумму чисел, которые делятся на $3$ или $5$
$\endgroup$
7
$\begingroup$
Есть нечто, называемое включением-исключением, которое вы хотите использовать: суммировать все целые числа до 100, удалить те, которые делятся на 3, удалить те, которые делятся на 5, затем добавить те, которые делятся на 15. =)
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Pop Video: Как сложить числа до 100 быстрее, чем ваш учитель
Расшифровка видео
Мы собираемся найти способ очень быстро сложить все числа от одного до 100, или 1000, или даже больше. Но сначала мы узнаем о блестящем немецком математике по имени Иоганн Карл Фридрих Гаусс, которому удалось разработать этот метод под влиянием момента, когда ему было около восьми лет, к большому неудовольствию своего учителя! Если бы не его нежелание полностью демонстрировать свои разработки, Гаусс, вероятно, был бы моим любимым математиком. Он родился в Германии в 1777 году и с самого раннего возраста проявлял невероятные способности к математике.
Например, говорят, что его мать, которая не умела ни читать, ни писать, никогда не записывала дату его рождения, но помнила, что он родился в среду и что это было за восемь дней до праздника Вознесения, год. В христианской традиции праздник Вознесения отмечается на 40-й день Пасхи, который каждый год сдвигается в зависимости от фаз луны.
Гаусс быстро использовал эту информацию, чтобы понять, что он должен был родиться 30 апреля. Но он не просто так сделал, он придумал хитрый способ вычислить дату Пасхи в любых прошедших и будущих годах.
Мне особенно нравится такой подход, когда я не просто отвечаю на максимально узкую интерпретацию заданного вопроса, а вместо этого вырабатываю общий подход, который можно использовать для ответов на подобные вопросы в будущем. Математику можно использовать для описания и понимания структуры и природы окружающего нас мира, чтобы мы могли делать прогнозы о нем в будущем. Я также восхищаюсь энтузиазмом и упорством Гаусса.
Многих бы просто разозлила мама, если бы она загадывала им сложный ребус в ответ на вопрос «Когда у меня день рождения?» Но он бодро решил проблему, а затем придумал общее решение множества подобных проблем. Когда мой восьмилетний сын спросил меня, сколько мне лет, я сказал: «Ну, через семь лет я впервые буду меньше чем в три раза старше тебя». Но он не удосужился разобраться с этим и сказал: «Хорошо, я просто спрошу у мамы».
Одним из великих ранних достижений Гаусса было то, что он показал, как с помощью циркуля и линейки можно построить правильные многоугольники, если число их сторон является произведением различных простых чисел Ферма и степени двойки. Он также сделал много других замечательных математических открытий, включая доказательство квадратичного закона взаимности, который позволяет нам увидеть, разрешимы ли квадратные уравнения в модульной арифметике. Он завершил важную работу над теоремой о простых числах, чтобы помочь нам увидеть, как простые числа распределяются среди целых чисел. Он не мог знать, насколько полезной станет такая работа в эпоху Интернета, поскольку мы используем простые числа, чтобы помочь нам зашифровать безопасные сообщения в интернет-транзакциях, и их лучшее понимание становится вопросом безопасности.
Он занимался различными типами геометрии, магнетизма, геодезическими исследованиями, делая астрономические расчеты намного проще и эффективнее, регрессионным анализом методом наименьших квадратов.
И статистическое нормальное распределение было названо в его честь распределением Гаусса. Короче говоря, мы все каждый день извлекаем пользу из его работы во всех отношениях: от статистических методов, используемых для оценки новых лекарств, до регрессионного анализа, используемого алгоритмами машинного обучения, которые помогают нам повысить эффективность и действенность нашего принятия решений.
Но то, что я хочу посмотреть в этом видео, это история о том, как, когда ему было всего восемь лет, Гаусс использовал свой блестящий математический ум, чтобы решить задачу, которую, по-видимому, поставил его учитель математики в качестве наказания. Как и в большинстве старых математических анекдотов, невозможно точно знать, что произошло. И в зависимости от того, где вы проводите свое исследование, вы найдете немного разные варианты этой истории и его возраста в то время. Но это моя любимая версия.
Часто говорят, что Гаусс был вундеркиндом. И его школьным учителям было довольно трудно иметь дело с ним, потому что он был очень беспокойным в классе, так много знал и так быстро соображал! В одной сказке рассказывается о том, как его учитель сказал ему сесть и сложить все числа от одного до 100, просто чтобы заставить его немного посидеть спокойно.
Они думали, что вычисление «один плюс два равно трем», «три плюс три равно шести», «шесть плюс четыре равно 10», «10 плюс пять равно 15», «15 плюс шесть равно 21» и т. путь до 100 займет у него целую вечность. Но он очень быстро вернулся с правильным ответом, 5050.
Вместо того, чтобы выполнять все вычисления по отдельности, Гаусс понял, что если он выпишет все числа от 1 до 100, то сможет организовать их в пары чисел, которые в сумме дают 101. Таким образом, один плюс 100 равно 101, два плюс 99 равно 101. , три плюс 98 равно 101, и так далее до 50 плюс 51 равно 101. Таким образом, у него было 50 пар, каждая из которых в сумме дает 101. Таким образом, общая сумма составит 50 лотов по 101 или 50 умножить на 101. Затем пять раз по 101 будет 505, а 10 умножить на 505 — это 5050. Работа сделана!
Это хороший метод, но давайте попробуем обобщить — можем ли мы описать метод или записать его в виде формулы, чтобы он работал для всех подобных задач? Ну, в этом примере мы суммировали 100 последовательных чисел.
И мы могли бы сгруппировать их в половину этого числа — это 50 пар чисел, каждое из которых в сумме дает 101, то есть сумму первого числа, единицы, плюс последнее число, 100, что в сумме дает 101. Итак, если мы обобщим и скажем, у нас есть 𝑛 чисел, а не конкретно 100 чисел, тогда мы можем математически записать наш метод.
Проще говоря, у нас есть сумма чисел от единицы до 𝑛 равна половине числа чисел — так что это количество пар — умноженное на сумму первого и последнего числа. Назовем эту сумму 𝑠, а количество чисел 𝑛. Таким образом, половина числа чисел 𝑛 больше двух. И умножаем это на сумму первого и последнего числа. Это единица, первая цифра, плюс 𝑛, последняя цифра, какой бы она ни была. Тогда общая формула состоит в том, что сумма 𝑠 равна 𝑛, умноженной на два, умноженных на один плюс 𝑛.
Теперь мы составим эту формулу, шаг за шагом представив выполненные нами вычисления. Но это оставляет нас, может быть, с небольшим беспокойством. Он работал нормально, когда у нас было четное количество элементов в списке, но будет ли он работать, если у нас будет нечетное количество элементов? Тогда в результате объединения чисел в середине останется еще одно число, которое нам нужно будет учитывать.
Давайте проиллюстрируем это меньшим списком, чтобы упростить задачу. Например, если мы сложим все целые числа от одного до пяти, у нас будет один плюс пять равно шести, два плюс четыре равно шести. Но тогда у нас останется это число в середине. Итак, если бы это было нашей отправной точкой для решения проблемы, мы бы сказали, что для пяти чисел мы можем заставить четыре из них соединиться в пары, чтобы создать две пары, и тогда у нас осталось бы это одно число в списке. середина. И эта тройка является средним значением первого и последнего числа в последовательности. Итак, один плюс пять, сложите их вместе, разделите на два, потому что там два числа. И получается шесть больше двух, что равно трем.
И если бы мы пытались вывести нашу общую формулу из этого хода мыслей, мы бы сказали, что сумма чисел равна сумме пар плюс среднее число. Теперь, какова сумма пар чисел? Итак, у нас есть пять чисел, и нам удалось использовать четыре из них, чтобы составить две пары. Таким образом, сколько бы чисел у нас ни было, 𝑛, если мы уменьшим их на единицу, это скажет нам, сколько чисел мы сможем соединить в пары.
И количество пар, поскольку каждая пара состоит из двух чисел, будет составлять половину этого числа. И сумма каждой пары по-прежнему равна первому числу плюс последнее число.
Итак, мы собираемся умножить это количество пар на сумму каждой пары, один плюс 𝑛. И мы сказали, что среднее число было просто средним значением первого и последнего числа. Итак, это один плюс 𝑛 последнее число, деленное на два. Теперь у меня есть общий делитель половины, который я могу разложить на множители. Итак, у меня есть половина, умноженная на 𝑛 минус один, умноженный на один плюс 𝑛 плюс один плюс 𝑛. Что ж, теперь у меня есть общий делитель один плюс 𝑛. Так что я собираюсь учесть это. И это оставит меня только с 𝑛 минус один в качестве первого члена в скобках и один в качестве следующего члена в скобках, потому что это всего лишь одна партия из одного плюс 𝑛. Поэтому я изменил формулу на половину от одного плюс 𝑛 умножить на 𝑛 минус один плюс один.
Ну, поскольку здесь мы просто складываем и вычитаем, я могу убрать эти скобки и оставить 𝑛 минус один плюс один.
И, конечно, если я вычитаю один, а затем добавляю один, это ничего. Итак, внутри этой скобки это просто упрощается до 𝑛. И, конечно же, если у меня просто есть 𝑛 в скобках, мне на самом деле даже скобки не нужны. Итак, моя сумма — мы назвали 𝑠 — равна половине одного плюс 𝑛 умножить на 𝑛. Ну, опять же, я могу переставить это. И мы получаем ту же формулу, что и в прошлый раз.
Итак, есть ли у нас четное или нечетное количество терминов, мы все равно можем использовать одну и ту же формулу для сложения всех этих чисел. Теперь не имеет значения, складываю ли я числа один, два, три до 100 или делаю это в обратном порядке, от 100, 99, 98 до единицы. Поэтому я написал оба метода здесь. И если я сложим эти две строки вместе, у меня будет 𝑠 плюс 𝑠, что даст мне два 𝑠. Итак, у меня есть удвоенная сумма чисел от одного до 100, равная 101 плюс 101 плюс 101, и так далее, и так далее 100 раз. И это означает, что удвоенная сумма будет равна 100, умноженной на 101. Другими словами, удвоенная сумма, которую я ищу, равна 10100.
Итак, если я разделю обе эти части на два, я обнаружу, что сумма этих чисел равна 5050, это ответ, который я получил раньше.
Но важно то, что если я обобщу эту формулу, у меня не будет никаких проблем с нечетным или четным количеством терминов, потому что я использую каждый термин в последовательности. Итак, выписав сумму чисел от единицы до 𝑛 в прямом и обратном порядке, а затем сложив эти две строки вместе, во-первых, мы получим 𝑠 плюс 𝑠 равно двум 𝑠. Тогда один плюс 𝑛 равен одному плюс 𝑛. Два плюс 𝑛 минус один, ну два минус один равно один. Так что это только один плюс 𝑛 снова. Три плюс 𝑛 минус два, ну три отнять два будет один. Итак, у нас снова один плюс 𝑛 и так далее. И тогда мы получаем 𝑛 минус два плюс три. Ну, минус два плюс три будет один. Итак, снова у нас есть 𝑛 плюс один или один плюс 𝑛 и так далее. Таким образом, мы получаем, что сумма, умноженная на два, равна 𝑛 лотов один плюс 𝑛 или 𝑛 умножить на один плюс 𝑛.
А затем, если я разделю обе части на два, получится та же формула, которую мы получили раньше, но с использованием другого метода.
Таким образом, использование этого другого метода помогло нам проверить правильность формулы. Однако полезное отличие этого метода заключалось в том, что он, казалось, не вызывал никакой путаницы, четное или нечетное количество членов в последовательности.
Но, наконец, давайте попробуем визуализировать проблему еще по-другому, нарисовав узор точками. Скажем так, мы хотим суммировать числа от одного до пяти. Мы можем представить эти числа, используя строки из одной, затем двух, затем трех, четырех, затем пяти точек: один, два, три, четыре, пять. Итак, у нас есть треугольник из точек, пять строк в высоту и 5 столбцов в ширину. Как мы можем легко посчитать, сколько точек у него есть? Ну, один из способов — повторить шаблон. Затем мы можем повернуть второй треугольник из точек на 180 градусов и сдвинуть его сюда.
Теперь у нас есть прямоугольник из точек с пятью столбцами и пятью плюс одна строками. У нас в два раза больше точек, чем нужно. Но что более важно, они образуют красивый прямоугольный рисунок, что облегчает их подсчет.
В этой конфигурации нам просто нужно сделать пять раз по шесть, чтобы получить 30 точек. Но количество точек, которые мы ищем, составляет половину этого числа. Полтора раза по 30 равно 15. Итак, синих точек было 15 или, другими словами, суммирование чисел от одного до пяти дает нам 15.
Теперь давайте обобщим это на 𝑛 строк в нашем треугольнике. Я знаю, что это похоже на пять рядов. Но представьте, что их намного больше, и мы не знаем, сколько их. Есть 𝑛 столбцов и 𝑛 плюс одна строка, где мы берем эту копию нашего треугольника из точек и превращаем их в прямоугольный узор. Итак, суммируя удвоенное количество точек, которое мы хотим, это удвоенная сумма, мы собираемся сделать 𝑛 раз 𝑛 плюс один. Как мы уже сказали, это в два раза больше точек, которые мы искали. Таким образом, деление пополам, которое дает нам сумму, равно 𝑛, умноженной на два, умноженных на 𝑛 плюс один. А теперь у нас есть третий способ придумать ту же формулу и, конечно же, проверить нашу работу.
Теперь, когда мы визуализируем проблему таким образом и думаем о том, когда 𝑛 равно единице, двум, трем и так далее, мы получаем серию паттернов.
Leave a Reply