Дано натуральное число приписать к нему такое же число: написать программу на языке паскаля 1)Дано натуральное число. Определить является ли оно чётным 2)дано натуральное число.
отвечен 28 Апр ’16 15:06
§2. Цифры. Десятичная запись натуральных чисел
ПОВТОРЯЕМ ТЕОРИЮ6. Заполните пропуски.
1) Натуральные числа записывают с помощью специальных знааков, которые называют цифрами.
2) Существует 10 цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
3) Натуральные числа, записанные одной цифрой, называют однозначными, двумя цифрами — двухзначными, тремя цифрами — трехзначными.
4) Все числа, кроме однозначных, называют многозначными.
5) Первой в записи натурального числа не может стоять цифра 0.
6) Чтобы прочитать натуральное число, цифры его записи разбивают справа налево на группы по 3 цифры, эти группы называют классами.
7) Первый справа класс называют классом единиц, второй справа — классом десятков, третий — классом тысяч, четвертый — классом миллионов.
8) Каждый класс разбивается справа на лево на разряды: единицы, десятки, сотни.
9) Запись натуральных чисел, которой мы пользуемся, называют десятиной.
РЕШАЕМ ЗАДАЧИ
7. Запишите в таблицу число:
1) тридцать пять миллиардов триста сорок шесть миллионов шестьсот шестнадцать тысяч двести семьдесят семь.
2) семьсот тридцать три миллиарда двести пять миллионов пятьдесят шесть тысяч шестьдесят четыре.
3) двадцать миллиардов сорок тысяч девяносто.
4) двести три миллиарда пятьсот семьдесят девять тысяч сто.
5) восемь миллиардов пять миллионов двенадцать тысяч девятнадцать.
6) два миллиарда три тысячи один.
8. Запишите, как читается число.
1) 4 328 176 214
2) 3 020 004 400
1) 4 миллиарда 328 миллионов 176 тысяч 214
2) 3 миллиарда 020 миллионов 004 тысячи 400
9. Запишите число в виде суммы разрядных слагаемых.
1) 5 491 268 = 5*1 000 000+4*100 000+9*10 000+1*1000+2*100+6*10+8*1
2) 2 790 321 = 2*1 000 000+7*100 000+9*10 000+0*1000+3*100+2*10+1*1
3) 6 003 807 = 6*1 000 000+0*100 000+0*10 000+3*1000+8*100+0*10+7*1
10. Запишите число, составленное из тех же цифр, что и данное, но рассположенных в обратном порядке.
Запишите число, составленное из тех же цифр, что и данное, но рассположенных в обратном порядке.
1) 1 234 — 4 321
2) 50 006 — 60 005
3) 1 000 678 — 8 760 001
11. Припишите справа к данному числу число, составленное из тех же цифр, что и данное. Прочитайте полученное число и представьте его в виде суммы разрядных слагаемых.
12. Запишите все двузнычные числа, для записи которых используются только цифры 3, 6 и 8 (цифры могут повторяться).
33, 36, 63, 66, 68, 83, 86, 88, 38
13. Сколько существует двузначных чисел, у которых первая цифра больше второй?
В первом десятке двузначных чисел такое число только одно — 10.
Во втором десятке таких чисел два. И т.д. в девятом десятке таких чисел 9.
1+2+3+4+5+6+7+8+9 = 10*4+5 = 45
Ответ: 45 (сорок пять).
14. В алфавите племени «амам» используется только две буквы — «а» и «м». Запишите все слова, содержащие три буквы, которые можно составить, используя алфавит этого племени.
ааа, аам, ама, маа, амм, мам, мма, ммм
15. Вставьте пропущенные числа.
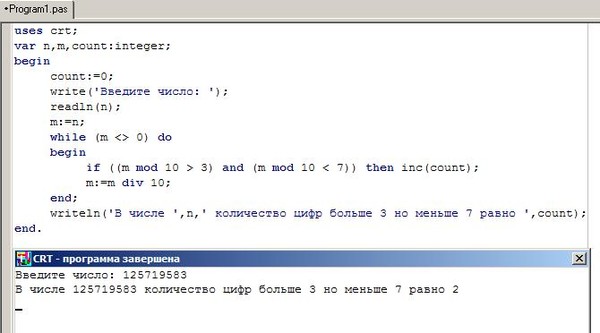
Цифры трехзначного числа, операции div и mod
На предыдущей странице мы рассматривали задачу отделения цифр от двузначного числа. На этой странице решаем задачи Integer9 — Integer16 из задачника Абрамяна, в которых займёмся работой с цифрами трехзначного числа.
Integer9. Дано трехзначное число. Используя одну операцию деления нацело, вывести первую цифру данного числа (сотни).
Для примера возьмем трехзначное число 671. Если его разделить на 100 и отбросить остаток, то получим 6 — первая цифра (число сотен). Поскольку для целочисленного деления существует операция div, то здесь достаточно вычислить 671div 100, что возвратит нам результат 6. Аналогично мы поступали при вычислении первой цифры двузначного числа в программе Integer6, только там нужно было делить на 10. Этот способ используется и в данной программе.
Код Pascal
|
Integer10. Дано трехзначное число. Вывести вначале его последнюю цифру (единицы), а затем — его среднюю цифру (десятки).
Код Pascal
|
Integer11. Дано трехзначное число. Найти сумму и произведение его цифр.
Код Pascal
|
Integer12. Дано трехзначное число. Вывести число, полученное при прочтении исходного числа справа налево.
Код Pascal
|
Второй вариант не предусматривает дополнительных переменных для хранения цифр числа:
Код Pascal
|
Integer13. Дано трехзначное число. В нем зачеркнули первую слева цифру и приписали ее справа. Вывести полученное число.
Дано трехзначное число. В нем зачеркнули первую слева цифру и приписали ее справа. Вывести полученное число.
Код Pascal
|
Integer14. Дано трехзначное число. В нем зачеркнули первую справа цифру и приписали ее слева. Вывести полученное число.
Код Pascal
|
Integer15. Дано трехзначное число. Вывести число, полученное при перестановке цифр сотен и десятков исходного числа (например, 123 перейдет в 213).
Код Pascal
|
Второй вариант решения задачи Integer15 – это аналог второго способа решения Integer12:
Код Pascal
|
Integer16. Дано трехзначное число. Вывести число, полученное при перестановке цифр десятков и единиц исходного числа (например, 123 перейдет в 132).
Первый вариант:
Код Pascal
|
Второй вариант:
Код Pascal
|
С++. Задачи с решениями. Числа и циклы.
С++. Задачи с решениями. Числа и циклы.
Числа и циклы.
- Составьте программу, выводящую на экран квадраты чисел от 10 до 20 включительно. Решение
- Даны натуральные числа от 35 до 87. Вывести на консоль те из них, которые при делении на 7 дают остаток 1, 2 или 5. Решение
- Найдите сумму , где число вводится пользователем с клавиатуры. Решение
- Найдите произведение цифр трехзначного числа. Решение
- Найдите количество четных цифр данного натурального числа. Решение
- Найдите наибольшую цифру данного натурального числа. Решение
- Найдите все четырехзначные числа, сумма цифр каждого из которых равна 15. Решение
- Определите, является ли натуральное число простым. Таблица простых чисел Что такое простое число Решение
- Найдите все делители данного натурального числа. Решение
- Даны и . Вычислите без использования логарифма и экспоненты. Решение
- В последовательности целых чисел найдите минимальное число и количество его повторений.
 Решение
Решение - На плоскости задан круг с центром в начале координат и набор точек. Его радиус, количество точек и их координаты вводятся с клавиатуры. Найдите точку вне круга, ближайшую к нему. Решение
- Вдоль координатной прямой размещены отрезков. Каждый отрезок задается координатами начала и конца и . Нужно найти какую-либо точку, принадлежащую всем отрезкам, или сообщить, что таких точек нет. Решение
- Отрезок последовательности целых чисел образует числа, идущие в ней подряд. Найдите номера чисел, которыми начинается и заканчивается отрезок с максимальной суммой, а также эту сумму. Решение
- Вам нужно разбить бронированные плиты на оборонной башне противника, которая в плане имеет вид -угольника. Для каждой стороны известно количество прикрывающих ее плит. Стрельба ведется из специальной двуствольной пушки — она ездит по рельсам вокруг башни и за один выстрел разбивает (по вашему желанию) или две плиты на одной стороне башни, или по одной плите на двух соседних сторонах.
 Найдите наименьшее число выстрелов, необходимых для разрушения всех плит.
Найдите наименьшее число выстрелов, необходимых для разрушения всех плит.
Вход. В первой строке текста — количество тестов , в каждой из следующих строк — тест. Тест задает число сторон и целых неотрицательных чисел — количества плит на сторонах. Решение - Стрелки часов движутся с постоянными угловыми скоростями и показывают часов минут. Найдите число полных минут до ближайшего момента, в который стрелки совпадут. Решение
- Строка состоит из клеток, пронумерованных от 1 до . Состояние клетки можно изменить — если она пуста, поставить в нее шашку (занять ее), иначе убрать из нее шашку (освободить ее). Вначале строка пуста. Нужно занять все клетки, соблюдая следующее правило. Изменение клетки допустимо, если она имеет номер 1 или расположена непосредственно после занятой клетки, имеющей минимальный номер среди занятых клеток. Решение
- Разбить последовательность чисел от 1 до на подпоследовательностей так, чтобы все они состояли из чисел и имели равные суммы.
 Если решений несколько, то вывести любое из них. Решение
Если решений несколько, то вывести любое из них. Решение - Составить программу поиска всех решений ребуса VOLVO + FIAT = MOTOR. Разным буквам соответствуют разные цифры, одинаковым — одинаковые. Старшая цифра каждого числа отличается от нуля. Решение
- Каждое натуральное число , однозначно раскладывается в произведение простых сомножителей, например, , , . Разложите натуральное число на простые множители (факторизация числа). Решение
к списку задач
Метки задачи, циклы. Смотреть запись.
Программа Python Расчет суммы и среднего первых n натуральных чисел
Как найти сумму и среднее значение первых n натуральных чисел в Python? В этой статье мы собираемся написать код Python для вычисления суммы и среднего положительных чисел, начиная с 1 до заданного числа (n), используя цикл for.
Цели данной статьи :
- Вычислите сумму и среднее первых n натуральных чисел , используя функцию цикла и диапазона .
- Вычислите сумму и среднее первых n натуральных чисел, используя математическую формулу в программе.
- Вычислить сумму и среднее значение любых введенных пользователем чисел .
- Вычислить сумму и среднее значение данного списка в Python
- Вычислить сумму с помощью встроенной функции суммы в Python
Теперь давайте посмотрим каждую по очереди.
Алгоритм вычисления суммы и среднего первых n натуральных чисел
- Позволяет пользователю ввести число (n), которое он хочет вычислить для суммы и среднего. Программа принимает вводимые пользователем данные с помощью функции ввода.
- Затем выполните цикл до введенного числа, используя цикл for и функцию range ().
- Затем вычислите сумму по формуле
сумма = сумма + текущее число. - Наконец, после завершения цикла, вычислите среднее значение, используя среднее значение
= сумма / п.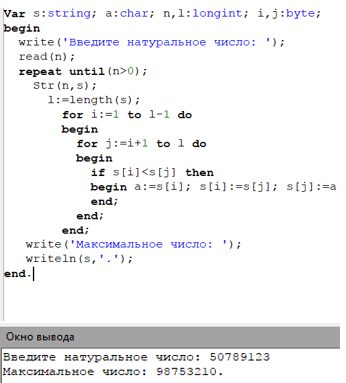
n— это номер, введенный пользователем.
Программа Python для вычисления суммы
п = 10
сумма = 0
для числа в диапазоне (0, n + 1, 1):
сумма = сумма + число
print («СУММА первых», n, «числа:», сумма) Выход :
Сумма первых 10 чисел: 55
Примечание. Приведенная выше программа выполняет цикл от 1 до числа, введенного пользователем, и добавляет все числа к сумме переменной .
Python Программа для расчета среднего значения
print («вычислить среднее первых n натуральных чисел»)
п = 10
средний = 0
сумма = 0
для числа в диапазоне (0, n + 1,1):
сумма = сумма + число;
среднее = сумма / п
print («Среднее от первого», n, «натуральное число:», среднее) Выход :
вычислить среднее значение первых n натуральных чисел Среднее значение первых 10 натуральных чисел: 5.5
Вычислить сумму и среднее первых n натуральных чисел по формуле
В приведенной выше программе мы вычислили сумму и среднее значение, используя функцию цикла и диапазона.Давайте посмотрим, как вычислить сумму и среднее значение напрямую с помощью математической формулы .
Сумма первых n натуральных чисел = n * (n + 1) / 2 , для n натуральное число.
среднее значение первого n натурального числа = (n * (n + 1) / 2) / n
Давайте теперь посмотрим на пример.
п = 10
сумма = п * (п + 1) / 2
среднее = (n * (n + 1) / 2) / n
print ("Сумма первых", n, "натуральные числа по формуле:", сумма)
print ("Среднее от первого", n, "натуральные числа по формуле:", среднее)
Выход :
Сумма первых 10 натуральных чисел по формуле: 55.0 Среднее значение первых 10 натуральных чисел по формуле: 5,5
Вычислить сумму и среднее значение нескольких введенных пользователем чисел
Например, вы хотите вычислить сумму и среднее значение любых пяти чисел, введенных пользователем . то есть, если вы хотите рассчитать сумму и среднее значение или процент от нескольких введенных пользователем чисел, обратитесь к следующей программе.
то есть, если вы хотите рассчитать сумму и среднее значение или процент от нескольких введенных пользователем чисел, обратитесь к следующей программе.
числа = ввод ("Введите числа, разделенные пробелом")
numberList = числа.Трещина()
печать ("\ п")
print ("Все введенные числа", numberList)
# Вычисление суммы всех введенных пользователем чисел
сумма1 = 0
для числа в numberList:
sum1 + = int (число)
print ("Сумма всех введенных чисел =", сумма1)
# Вычисление среднего числа всех введенных пользователем чисел
среднее = сумма1 / лен (числоСписок)
print ("Среднее из всех введенных чисел =", среднее)
Выход :
Введите числа через пробел 5 10 15 20 25 Все введенные числа ['5', '10', '15', '20', '25'] Сумма всех введенных чисел = 75 Среднее значение всех введенных чисел = 15.0
Подробнее о том, как принять список в качестве ввода от пользователя.
Вычислить сумму и среднее значение данного списка в Python
Допустим, у вас есть список чисел, и вы хотите вычислить сумму чисел, присутствующих в списке.
- Все, что вам нужно сделать, это перебрать список с помощью цикла for и добавить каждое число в переменную суммы.
- Чтобы вычислить среднее значение, разделите сумму на длину данного списка (общее число в списке)
Давайте посмотрим на это на примере.
Программа 1:
сумма = 0
список = [11,22,33,44,55,66,77]
для числа в списке:
сумма = сумма + число
среднее = сумма / длина (список)
print ("сумма элементов списка:", сумма)
print ("Среднее значение элемента списка", среднее) Выход :
сумма элементов списка: 308 Среднее значение элемента списка составляет 44,0
Вычислить сумму с помощью встроенной функции суммы в Python
Давайте посмотрим, как использовать функцию sum () для вычисления суммы.
print («Сумма диапазона чисел:», sum (range (1, 5))) Выход :
Сумма диапазона чисел: 10
Python цикл while для вычисления суммы и среднего
Вы также можете использовать цикл while для вычисления суммы и среднего n чисел.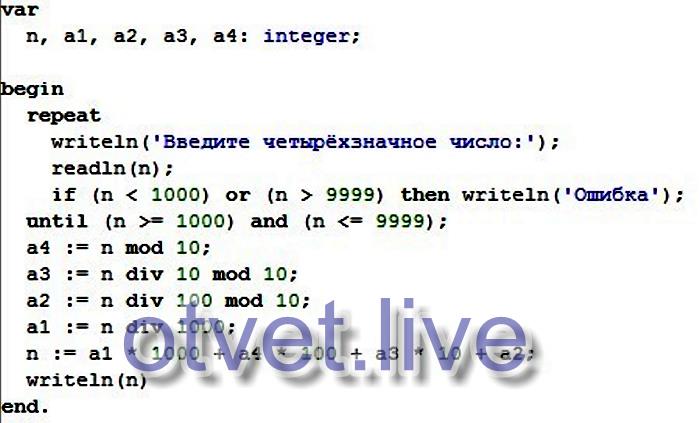 Здесь n может быть 2, 5 или любым числом. Выполните следующие действия:
Здесь n может быть 2, 5 или любым числом. Выполните следующие действия:
- Возьмем значение n = 20
- Выполнить цикл while, пока n не станет больше нуля
- Добавьте текущее значение n к суммируемой переменной.Кроме того, уменьшите n на 1 в теле цикла
- вычисляет среднее значение путем деления суммы на общее количество.
Давайте посмотрим на демонстрацию, чтобы вычислить сумму и среднее значение с помощью цикла while.
п = 20
total_numbers = n
сумма = 0
в то время как (n> = 0):
сумма + = п
n- = 1
print ("сумма с использованием цикла while", сумма)
среднее = сумма / всего_числа
print («Среднее с использованием цикла while», среднее) Выход :
Суммас использованием цикла 210 Среднее с использованием цикла while 10.5
Практическая задача: добавить две матрицы в Python
matrixOne = [[6,9,11],
[2, 3,8]]
matrixTwo = [[15,18,11],
[26,16,19]]
результат = [[0,0,0],
[0,0,0]]
# Первая итерация строк
для i в диапазоне (len (matrixOne)):
# Вторая итерация столбцов
для j в диапазоне (len (matrixOne [0])):
результат [i] [j] = matrixOne [i] [j] + matrixTwo [i] [j]
print («Сложение двух матриц в Python»)
для res в результате:
печать (разрешение) Двоичные, обратные и дополнительные коды
Наш пользователь попросил создать онлайн-калькулятор для преобразования введенного целого числа в его двоичную форму, а также отображать его обратные и дополнительные коды / 743/
Ниже представлен калькулятор, который выполняет эту задачу. Он принимает положительные или отрицательные целые числа и выводит вышеупомянутые двоичные коды.
Он принимает положительные или отрицательные целые числа и выводит вышеупомянутые двоичные коды.
Под калькулятором, как обычно, объясняется, что все это значит.
Обновление : Из комментариев я вижу, что люди неправильно интерпретируют результаты калькулятора. Моя ошибка. Калькулятор просто применял описанный алгоритм к любому введенному числу. Сейчас меняю, чтобы не было путаницы. То есть для положительных чисел он показывает двоичное представление числа (потому что нет обратного или комплиментарного для положительного), а для отрицательного числа он показывает его представление из положительного в обратном и дополнительном кодах.
Двоичный, обратный и дополнительный коды
Обратный код (дополнение до единицы)
Дополнительный код (дополнение до двух)
content_copy Ссылка сохранить Сохранить расширение Виджет
Итак, немного теории
Двоичный код — это двоичное представление целого числа без знака. Если мы говорим о компьютерах, для представления числа используется определенное количество битов.Итак, общий диапазон, который может быть представлен n-битами, составляет
Если мы говорим о компьютерах, для представления числа используется определенное количество битов.Итак, общий диапазон, который может быть представлен n-битами, составляет
Обратный код или с дополнением до единицы — это просто инвертированный двоичный код числа. То есть все нули становятся единицами, а все единицы — нулями.
Дополнительный код или Дополнение до двух является обратным кодом плюс один
Итак, о чем все?
Эти коды были придуманы, чтобы сделать работу со знаками более удобной (для машин). Поскольку я из тех людей, которые любят учиться на примерах, я объясню это утверждение на примерах.
Предположим, у нас есть компьютер с 4-битными двоичными числами. Общий диапазон, который может быть представлен 4-мя битами, составляет 16 — 0,1, … 15
00 — 0000
…
15 — 1111
Но это беззнаковые числа и от них мало толку. Нам нужно ввести знак. Итак, половина диапазона берется за положительные числа (восемь, включая ноль), а половина диапазона — за отрицательные (также восемь). Обратите внимание, что машина считает ноль положительным числом, в отличие от обычной математики.
Итак, половина диапазона берется за положительные числа (восемь, включая ноль), а половина диапазона — за отрицательные (также восемь). Обратите внимание, что машина считает ноль положительным числом, в отличие от обычной математики.
Итак, наши положительные результаты — 0 ,…, 7, а отрицательные — -1, …, — 8.
Чтобы различать положительные и отрицательные числа, мы назначаем крайний левый бит знаковый бит . Нулевой знаковый бит говорит о том, что это положительное число, а единица — отрицательное.
Положительные числа представлены в виде простого двоичного кода
0 — 0000
1 — 0001
…
7 — 0111
Но как можно представить отрицательные числа? А вот и дополнительный код.
То есть дополнение -7 — это
двоичное 7 = 0111
обратное 7 = 1000
дополнение 7 = 1001
Обратите внимание, что двоичный код 1001 равен 9, что отличается от -7 на 16, или.Или, что то же самое, дополнительный код «дополняет» двоичный код до, например, 7 + 9 = 16
Это оказалось очень полезным для машинных вычислений — использование дополнительного кода для представления отрицаний позволяет инженерам использовать схему сложения как для сложения, так и для вычитания, что упрощает конструкцию ALU (арифметическая и логическая единица — часть процессора). Кроме того, это представление легко обнаруживает переполнение, когда не хватает битов для представления данного числа.
Кроме того, это представление легко обнаруживает переполнение, когда не хватает битов для представления данного числа.
Несколько примеров
7-3 = 4
0111 двоичное 7
1101 дополнение до двух 3
0100 результат сложения 4
-1 + 7 = 6
1111 дополнение до двух 1
0111 двоичное 7
0110 результат сложения 6
Переполнение обнаруживается при просмотре двух последних переносов, включая перенос за крайний правый бит.Если биты переноса 11 или 00, переполнения нет, если биты переноса 01 или 10, переполнение происходит. И, если нет переполнения, перенос за крайний правый бит можно игнорировать.
Некоторые примеры с переносами и пятым битом (бит за крайним правым битом)
7 + 1 = 8
00111 двоичный 7
00001 двоичный 1
01110 несет
01000 результат сложения 8 — переполнение
Два последних переноса — 01. Это дает сигнал о переполнении.
-7 + 7 = 0
00111 двоичный 7
01001 два дополнения к 7
11110 несет
10000 результат сложения 16 — но пятый бит можно игнорировать, реальный результат равен 0
Два последних переноса — 11. Переполнения нет, поэтому правильный результат равен нулю.
Переполнения нет, поэтому правильный результат равен нулю.
Проверка переполнения может быть выполнена простой операцией XOR над двумя последними битами переноса.
Из-за этих удобных свойств дополнение до двух является наиболее распространенным методом представления отрицательных чисел на компьютерах.
П.С. Обратный код или дополнение до единицы «дополняет» двоичный код до (всех). Его также можно использовать для представления отрицательных значений, но схема сложения должна использовать циклический перенос и является более сложной. Кроме того, диапазон, который может быть представлен n-битами, уменьшается на 1, поскольку 1111 занято как инвертированное 0000 — отрицательный ноль.Так что это менее удобно.
CCNA 1 Introduction to Networks v6.0 — ITN Chapter 8 Exam Answers
Как найти: Нажмите «Ctrl + F» в браузере и введите любую формулировку вопроса, чтобы найти этот вопрос / ответ.
ПРИМЕЧАНИЕ. Если у вас есть новый вопрос по этому тесту, прокомментируйте список вопросов и множественный выбор в форме под этой статьей. Мы обновим для вас ответы в кратчайшие сроки.Спасибо! Мы искренне ценим ваш вклад в наш сайт.
Если у вас есть новый вопрос по этому тесту, прокомментируйте список вопросов и множественный выбор в форме под этой статьей. Мы обновим для вас ответы в кратчайшие сроки.Спасибо! Мы искренне ценим ваш вклад в наш сайт.
- Что происходит при соединении двух или более коммутаторов вместе?
- Увеличено количество широковещательных доменов.
- Увеличен размер широковещательного домена. *
- Количество коллизионных доменов уменьшено.
- Размер области коллизии увеличен.
Explain:
Когда два или более коммутатора соединяются вместе, размер широковещательного домена увеличивается, а вместе с ним увеличивается и количество конфликтных доменов.Количество широковещательных доменов увеличивается только при добавлении маршрутизаторов. - См. Выставку. Сколько существует широковещательных доменов?
Объясните:
Маршрутизатор используется для маршрутизации трафика между разными сетями. Широковещательному трафику не разрешено пересекать маршрутизатор, и поэтому он будет содержаться в соответствующих подсетях, откуда он исходит.
Широковещательному трафику не разрешено пересекать маршрутизатор, и поэтому он будет содержаться в соответствующих подсетях, откуда он исходит. - По каким двум причинам сетевой администратор может захотеть создать подсети? (Выберите два.)
- упрощает проектирование сети
- повышает производительность сети *
- проще реализовать политики безопасности *
- уменьшение количества необходимых маршрутизаторов
- уменьшение количества необходимых переключателей
Explain:
Две причины для создания подсетей включают уменьшение общего сетевого трафика и повышение производительности сети. Подсети также позволяют администратору реализовывать политики безопасности на основе подсетей.На количество маршрутизаторов или коммутаторов это не повлияет. Подсети не упрощают структуру сети. - См. Выставку. Компания использует для своей сети адресный блок 128.
 107.0.0/16. Какая маска подсети могла бы обеспечить максимальное количество подсетей одинакового размера, обеспечивая при этом достаточное количество адресов узлов для каждой подсети на выставке?
107.0.0/16. Какая маска подсети могла бы обеспечить максимальное количество подсетей одинакового размера, обеспечивая при этом достаточное количество адресов узлов для каждой подсети на выставке? - 255.255.255.0
- 255.255.255.128 *
- 255.255.255.192
- 255.255.255,224
- 255.255.255.240
Explain:
Самая большая подсеть в топологии состоит из 100 хостов, поэтому маска подсети должна содержать не менее 7 битов хоста (27-2 = 126). 255.255.255.0 имеет 8 бит хостов, но это не соответствует требованию предоставления максимального количества подсетей. - См. Выставку. Сетевой администратор назначил LAN LBMISS диапазон адресов 192.168.10.0. Этот диапазон адресов разбит на подсети с использованием префикса / 29.Чтобы приспособить новое здание, техник решил использовать пятую подсеть для настройки новой сети (нулевая подсеть является первой подсетью).
 В соответствии с политиками компании интерфейсу маршрутизатора всегда назначается первый используемый адрес хоста, а серверу рабочей группы дается последний используемый адрес хоста. Какую конфигурацию следует ввести в свойствах сервера рабочей группы, чтобы разрешить подключение к Интернету?
В соответствии с политиками компании интерфейсу маршрутизатора всегда назначается первый используемый адрес хоста, а серверу рабочей группы дается последний используемый адрес хоста. Какую конфигурацию следует ввести в свойствах сервера рабочей группы, чтобы разрешить подключение к Интернету? - IP-адрес: 192.168.10.65 маска подсети: 255.255.255.240, шлюз по умолчанию: 192.168.10.76
- IP-адрес: 192.168.10.38 маска подсети: 255.255.255.240, шлюз по умолчанию: 192.168.10.33
- IP-адрес: 192.168.10.38 маска подсети: 255.255.255.248, шлюз по умолчанию: 192.168.10.33 *
- IP-адрес: 192.168.10.41 маска подсети: 255.255.255.248, шлюз по умолчанию: 192.168.10.46
- IP-адрес: 192.168.10.254 маска подсети: 255.255.255.0, шлюз по умолчанию: 192.168.10.1
Объяснение:
Использование префикса / 29 для подсети 192.168.10.0 приводит к подсетям, которые увеличиваются на 8:
192.168. 10.0 (1)
10.0 (1)
192.168.10.8 (2)
192.168.10.16 (3)
192.168.10.24 (4)
192.168.10.32 (5) - Если сетевое устройство имеет маску / 28, сколько IP-адресов доступно для хостов в этой сети?
Объяснение:
Маска A / 28 такая же, как 255.255.255.240. Остается 4 бита хоста. С 4 битами хоста возможны 16 IP-адресов, но один адрес представляет номер подсети, а один адрес представляет широковещательный адрес.Затем можно использовать 14 адресов для назначения сетевым устройствам. - Какая маска подсети будет использоваться, если доступно 5 бит хоста?
- 255.255.255.0
- 255.255.255.128
- 255.255.255.224 *
- 255.255.255.240
Объяснение:
Маска подсети 255.255.255.0 имеет 8 бит хоста. Маска 255.255.255.128 дает 7 бит хоста. Маска 255.255.255.224 имеет 5 бит хоста.Наконец, 255.255.255.240 представляет 4 бита хоста.
- Сколько адресов хостов доступно в сети 172.16.128.0 с маской подсети 255.255.252.0?
- 510
- 512
- 1022 *
- 1024
- 2046
- 2048
Объясните:
Маска 255.255.252.0 равна префиксу / 22. Префикс A / 22 предоставляет 22 бита для сетевой части и оставляет 10 бит для хост-части.10-2 = 1022). - Сколько битов необходимо заимствовать из хостовой части адреса, чтобы разместить маршрутизатор с пятью подключенными сетями?
Explain:
Каждая сеть, которая напрямую связана с интерфейсом на маршрутизаторе, требует своей собственной подсети. Формула 2n, где n — количество заимствованных битов, используется для вычисления доступного количества подсетей при заимствовании определенного количества битов. - Сетевой администратор хочет иметь одну и ту же сетевую маску для всех сетей на определенном небольшом сайте.
 На сайте есть следующие сети и количество устройств:
На сайте есть следующие сети и количество устройств:
IP-телефонов — 22 адреса
ПК — 20 необходимых адресов
Принтеры — 2 необходимых адреса
Сканеры — 2 адреса
Сетевой администратор посчитал, что 192.168.10.0/24 является быть сетью, используемой на этом сайте. Какая отдельная маска подсети наиболее эффективно использовала бы доступные адреса для использования в четырех подсетях?- 255.255.255.0
- 255.255.255.192
- 255.255.255.224 *
- 255.255.255.240
- 255.255.255.248
- 255.255.255.252
Объясните:
Если должна использоваться та же маска, тогда сеть с наибольшим количеством хостов должна быть проверена на количество хостов, которое в данном случае составляет 22 хоста. Таким образом, необходимо 5 бит хоста. Для этих сетей подходит маска подсети / 27 или 255.255.255.224. - Компания имеет сетевой адрес 192.
 168.1.64 с маской подсети 255.255.255.192. Компания хочет создать две подсети, которые будут содержать 10 и 18 хостов соответственно. Какие две сети смогли бы этого достичь? (Выберите два.)
168.1.64 с маской подсети 255.255.255.192. Компания хочет создать две подсети, которые будут содержать 10 и 18 хостов соответственно. Какие две сети смогли бы этого достичь? (Выберите два.) - 192.168.1.16/28
- 192.168.1.64/27*
- 192.168.1.128/27
- 192.168.1.96/28*
- 192.168.1.192/28
Объяснение:
Подсеть 192.168.1.64 / 27 имеет 5 битов, которые выделены для адресов хоста, и поэтому она сможет поддерживать 32 адреса, но только 30 действительных IP-адресов хоста.Подсеть 192.168.1.96/28 имеет 4 бита для адресов хоста и сможет поддерживать 16 адресов, но только 14 действительных IP-адресов хоста - Сетевой администратор периодически разбивает сеть на подсети. Самая маленькая подсеть имеет маску 255.255.255.248. Сколько используемых адресов хостов будет предоставлять эта подсеть?
Объясните:
Маска 255. 255.255.248 эквивалентна префиксу / 29. Это оставляет 3 бита для хостов, обеспечивая в общей сложности 6 используемых IP-адресов (23 = 8 — 2 = 6).
255.255.248 эквивалентна префиксу / 29. Это оставляет 3 бита для хостов, обеспечивая в общей сложности 6 используемых IP-адресов (23 = 8 — 2 = 6). - См. Выставку. Учитывая сетевой адрес 192.168.5.0 и маску подсети 255.255.255.224, сколько всего адресов узлов не используется в назначенных подсетях?
Объяснение:
Сетевой IP-адрес 192.168.5.0 с маской подсети 255.255.255.224 предоставляет 30 используемых IP-адресов для каждой подсети. Подсети A требуется 30 адресов хоста. Нет потерянных адресов. Подсеть B использует 2 из 30 доступных IP-адресов, потому что это последовательный канал.Следовательно, он теряет 28 адресов. Точно так же подсеть C тратит впустую 28 адресов. Подсети D требуется 14 адресов, поэтому она теряет 16 адресов. Общее количество потерянных адресов составляет 0 + 28 + 28 + 16 = 72 адреса. - См. Выставку. Учитывая уже используемые адреса и необходимость оставаться в пределах диапазона сети 10.
 16.10.0/24, какой адрес подсети можно назначить сети, содержащей 25 узлов?
16.10.0/24, какой адрес подсети можно назначить сети, содержащей 25 узлов? - 10.16.10.160/26
- 10.16.10.128/28
- 10.16.10.64 / 27 *
- 10.16.10.224/26
- 10.16.10.240/27
- 10.16.10.240/28
Объяснение:
Адреса с 10.16.10.0 по 10.16.10.63 используются для крайней левой сети. Адреса с 10.16.10.192 по 10.16.10.207 используются центральной сетью. Адресное пространство от 208 до 255 предполагает маску / 28, которая не позволяет разместить достаточно битов хоста для размещения 25 адресов хоста. Доступные диапазоны адресов включают 10.16. 10.64 / 26 и 10.16.10.128 / 26. Для размещения 25 хостов необходимо 5 бит хостов, поэтому необходима маска / 27. Четыре возможных подсети / 27 могут быть созданы из доступных адресов между 10.16.10.64 и 10.16.10.191:
10.16.10.64/27
10.16.10.96/27
10.16.10.128/27
10.16.10.160/27 - См.
 Выставку. Учитывая сетевой адрес 192.168.5.0 и маску подсети 255.255.255.224 для всех подсетей, сколько всего адресов хостов не используется в назначенных подсетях?
Выставку. Учитывая сетевой адрес 192.168.5.0 и маску подсети 255.255.255.224 для всех подсетей, сколько всего адресов хостов не используется в назначенных подсетях? - Сетевому администратору необходимо отслеживать сетевой трафик к серверам и от серверов в центре обработки данных.Какие функции схемы IP-адресации следует применять к этим устройствам?
- случайных статических адресов для повышения безопасности
- адресов из разных подсетей для резервирования
- предсказуемых статических IP-адресов для упрощения идентификации *
- динамических адресов для уменьшения вероятности дублирования адресов
Explain:
При мониторинге серверов сетевой администратор должен иметь возможность быстро идентифицировать их.Использование предсказуемой схемы статической адресации для этих устройств упрощает их идентификацию. Безопасность сервера, избыточность и дублирование адресов не являются особенностями схемы IP-адресации. - Какие две причины обычно делают DHCP предпочтительным методом назначения IP-адресов хостам в больших сетях? (Выберите два.)
- Устраняет большинство ошибок конфигурации адреса. *
- Это гарантирует, что адреса применяются только к устройствам, которым требуется постоянный адрес.
- Это гарантирует, что каждое устройство, которому нужен адрес, получит его.
- Он предоставляет адрес только тем устройствам, которым разрешено подключение к сети.
- Это снижает нагрузку на обслуживающий персонал сети. *
Explain:
DHCP обычно является предпочтительным методом назначения IP-адресов хостам в больших сетях, поскольку он снижает нагрузку на персонал службы поддержки сети и практически исключает ошибки ввода.Однако сам DHCP не делает различий между авторизованными и неавторизованными устройствами и назначает параметры конфигурации всем запрашивающим устройствам. DHCP-серверы обычно настраиваются для назначения адресов из диапазона подсети, поэтому нет гарантии, что каждое устройство, которому нужен адрес, получит его. - DHCP-сервер используется для динамического назначения IP-адресов хостам в сети. Пул адресов настроен как 192.168.10.0/24. В этой сети есть 3 принтера, которым необходимо использовать зарезервированные статические IP-адреса из пула.Сколько IP-адресов в пуле осталось назначить другим хостам?
Объясните:
Если блок адресов, выделенных для пула, равен 192.168.10.0/24, хостам в сети необходимо назначить 254 IP-адреса. Поскольку существует 3 принтера, адреса которых должны быть назначены статически, остается 251 IP-адрес для назначения. - См. Выставку. Компания развертывает схему адресации IPv6 для своей сети.В проектном документе компании указано, что часть IPv6-адресов подсети используется для нового иерархического дизайна сети, при этом подраздел сайта представляет несколько географических сайтов компании, раздел дочерних сайтов представляет несколько кампусов на каждом сайте, а подраздел сайта раздел подсети для обозначения каждого сегмента сети, разделенного маршрутизаторами. Какое максимальное количество подсетей достигается при такой схеме на подсайт?
Из одной в другую позиционную систему счисления
Обзор
«Если мы когда-нибудь встретимся с разумной формой жизни из космоса,
, который использует позиционную систему счисления в своей математике,
нам понадобится что-нибудь, чтобы быстро и точно перевести
в понятной нам системе счисления.»- Автор
Программа для преобразования чисел из одной в другую позиционную систему счисления была написана как «Приложение Windows Form» в среде Sharp Develop IDE на языке программирования C # вер. 4.0, и для ее работы необходима платформа Microsoft .Net версии 4.0 или выше. Графический интерфейс пользователя (GUI) интуитивно понятен и состоит из поля, текстового поля для ввода числа, которое вы хотите преобразовать, текстового поля для отображения результатов или преобразованного числа, четырех кнопок для увеличения или уменьшения основы системы счисления. , чтобы получить номер в желаемой многочисленной системе и трех текстовых сообщениях, текстовых метках, чтобы показать изменение числовой системы.В программе есть ограничение, когда под вопросом размер введенного числа для конвертации. Это ограничение вызвано ограничениями в языке программирования. Это максимальное количество цифр, которое программа может принять при преобразовании из десятичной системы счисления в другую. Таким образом, максимальное количество цифр, которое может содержать введенное число в десятичной системе, составляет 15, включая десятичную точку. Что касается перевода из других систем в десятичную систему счисления, введенное число ограничено 256 цифрами. Программный код с алгоритмом объясняется в этой статье, внизу находятся ссылки для скачивания полного решения для IDE Sharp Develop и программы.Изображение программы также является ссылкой на скачивание программы.
Ссылки для скачивания
Скачать полное решение для IDE Sharp Develop 4.1 с открытым кодом, написанным на C #. Скачав решение, вы можете открыть его в IDE Sharp Develop и собрать релизную версию программы. Если вы работаете в IDE (интегрированной среде разработки) другого типа, вы можете открыть всю документацию, содержащую волшебный код, и просто скопировать ее в свою программу.
Скачать проект с открытым исходным кодом
Если вы просто хотите использовать программу, вы можете скачать ее здесь.После загрузки просто нажмите на исполняемый файл. Важно, для корректной работы программе требуется Microsoft .Net framework 4.0 или выше.
Скачать программу
Введение
Математика — всегда интересная научная дисциплина со своими задачами, которые решает компьютер. «Преобразование чисел из одной позиционной системы счисления в другую» — это один из предметов, который можно использовать для обучения разработке алгоритма и компьютерной программы для решения этой и других подобных задач.
Так как я соблюдаю общий метод решения проблем с компьютерами, и эта проблема будет решена посредством конкретных шагов.
Шаг первый
Полный обзор и понимание процесса, для которого вы хотите создать компьютерную программу или написать псевдокод.
Шаг второй
Написание алгоритма на основе псевдокода.
Шаг третий
Кодирование на основе алгоритма на некоторых языках программирования, наиболее подходящих для этого типа программ.
Шаг четвертый
Программа тестирования и отладки.
Шаг пятый
Написание документации к программе, инструкции, лицензионного соглашения и патентования программного обеспечения.
Решение проблемы
Шаг первый
Исследование и глубокое понимание процесса преобразования чисел из одной позиционной системы счисления в другую.
Поиск по всему Интернету информации о том, как преобразовать число из одной в другую позиционную систему счисления, я нашел много интересных ссылок и статей, относящихся к этой теме.Что самое главное, все они объясняют процесс конвертации на простых математических примерах, понятных любому, кто имеет базовые математические знания. Я выбрал три статьи, на которых я основывал свое исследование и разработку псевдокода.
Первая «Система счисления», объясняющая все, что касается чисел,
Вторая «Система счисления», объясняющая все о системах счисления, и
Третье «позиционное обозначение», которое подробно объясняет позиционные системы счисления, включая преобразование.
Тщательно проанализируйте эти статьи, особенно последнюю. Здесь извлекается суть, которая нужна для решения проблемы.
Перевод из выбранной системы счисления в десятичную систему счисления (* — знак умножения):
система счисления с двумя цифрами:
1001,111 (2) = 1 * 2 3 + 0 * 2 2 + 0 * 2 1 + 1 * 2 907 0 + 1 * 2 -1 + 1 * 2 -2 + 1 * 2 -3 = 9,875 (10)
трехзначная система счисления:
1020,021 (3) = 1 * 3 3 + 0 * 3 2 + 2 * 3 1 + 0 * 3 907 0 + 0 * 3 -1 + 2 * 3 -2 + 1 * 3 -3 = 33,2592592592593 0003 (10) 907 система счисления с четырьмя цифрами: 1230,301 (4) = 1 * 4 3 + 2 * 4 2 + 3 * 4 1 + 0 * 4 907 0 + 3 * 4 -1 + 0 * 4 -2 + 1 * 4 -3 = 108,765625 (10) …………………………………………… ………………………………………….. ………………………………………….. ……………….. ………………………………………… ………………………………………….. ………………………………………….. ………………….. ………………………………………… ………………………………………….. ……………………………………………. ………………… десятизначная система счисления: 9870,567 (10) = 9 * 10 3 + 8 * 10 2 + 7 * 10 1 + 0 * 907 0 + 5 * 10 -1 + 6 * 10 -2 + 7 * 10 -3 = 9870,567 (10) система счисления с шестнадцатью цифрами: 8FEA, CD7 (16) = 8 * 16 3 + 15 * 16 2 + 14 * 16 1 + 10 * 16 0 + 12 * 16 -1 + 13 * 16 -2 + 7 * 16 -3 = 36842,80244 (10) Здесь мы можем увидеть общую формулу для преобразования чисел с основанием системы счисления X в десятичную систему счисления: ( (n) a (n-1) a (n-2) …a (1) a (0) , c (1) c (2) c (3) … c (m-2) c (m-1) ) c (м) ) (x) = = (Sum (a (k) * x (+ k) ) (k = n до k = 0) + Sum (c (j) * x (-j) ) (от j = 1 до j = м) ) (10) a — значение цифры внутри Целой части числа в виде числового значения в десятичной системе счисления n — позиция цифры внутри целой части числа c — значение цифры внутри фрактальной части числа в виде числового значения в десятичной системе счисления м — положение цифры внутри фрактальной части числа x — системное базовое значение выбранного числа для преобразования k — счетчик положения цифр внутри Целой части числа j — счетчик положения цифр внутри фрактальной части числа Уведомление: Результат преобразования в систему десятичных чисел является точным, только если число является рациональным, в противном случае он является приблизительным из-за округления до желаемого числа десятичных знаков.Есть ограничение на размер и точность чисел. Поскольку эта программа использует тип переменных «Double» для хранения значений чисел с плавающей запятой, ее точность составляет до 15-16 цифр, а приблизительный диапазон составляет от ± 5,0 × 10–324 до ± 1,7 × 10 + 308. По этому поводу должна быть больше исследовательской работы, с конечной целью, чтобы программа работала с абсолютной точностью. Теперь программа работает с точностью до пятнадцати цифр при переводе числа из другой в десятичную. И есть проблема с научным форматом представления чисел, который является автоматическим в некоторых языках программирования и не позволяет пользователю видеть все цифры в преобразованном числе !? Запуск программы Введите число, которое вы хотите преобразовать Введите основание системы счисления введенного числа Если это не число с плавающей запятой Преобразовать целую часть (перейти к шагу подпрограммы 1).Переходите к шагу 9. Отдельная целая часть числа от фрактальной части Преобразование составной части (переход к шагу подпрограммы 1) Преобразовать фрактальную часть (перейти к шагу подпрограммы 1) Соедините две переделанные детали Показать результат Конечная программа Присвойте значение A (A = значение цифры в целой части числа в позиции K, представленное как числовое значение в десятичной системе счисления) Конец подпрограммы Присвойте значение для C (C = цифра в фрактальной части числа в позиции K, представленная как числовое значение в десятичной системе счисления) Конец подпрограммы Преобразование из десятичной системы счисления в другую систему счисления. Преобразует десятичное число 512,125 в систему счисления с двумя цифрами, известную как двоичная система. (512,125) (10) = (?) (2) Отделить целую часть от фрактальной части числа. (Интеграл = 512, Фрактал = 0,125) Разделите целую часть числа на основание системы счисления, в которую вы хотите преобразовать число. Двоичная система счисления Основание — два. Integral / Base = Результат деления 512: 2 = 256,0 Отдельная составная часть результата деления, Интегральная часть результата деления = 256 Умножение результата деления на основание Целое число результата деления * База = результат 256 * 2 = 512 Вычтите интеграл и результат и запомните результат как последовательность шифров 512 — 512 = 0 Новый интеграл = 256 (интеграл = интеграл результата деления) Если Integral не равен нулю перейти к шагу 2 (условие остановки процесса преобразования) Прочитать последовательность шифрования в обратном направлении и получить двоичное число. Результат преобразования: 512 (10) = 1000000000 (2) Весь процесс более понятен благодаря этой таблице, просто следуйте заголовку таблицы. A Б К D E ф Неотъемлемая часть номера База для преобразования в (2) Неотъемлемая часть результата деления Интегральный / Базовый A / B Результат умножения Integral * Base C * B Результат вычитания Шифровальная последовательность A — D Прочитать последовательность шифрования в обратном направлении и получить двоичное число Целая часть числа преобразована в двоичную систему счисления 512 (10) = 1000000000 (2) 512 2 256 512 0 1 256 2 128 256 0 0 128 2 64 128 0 0 64 2 32 64 0 0 32 2 16 32 0 0 16 2 8 16 0 0 8 2 4 8 0 0 4 2 2 4 0 0 2 2 1 2 0 Предупреждение: я не знаю, действительно ли это работает, это просто идея, скажите мне, если я ошибаюсь 🙂 Сначала всего, что нам нужно отсортировать в массиве.Подсчитаем количество плохих треугольников. Плохой треугольник определяется как кортеж ( i , j , k ), с i < j < k и L [ i ] + L [ j ] <= L [ k ] (где L [ i ] = длина i-го стержня). Заметим, что максимальная сумма для L [ i ] + L [ j ] составляет 10 6 . Отметим Ways [ S ] — количество способов выразить S как сумму двух чисел из массива, Freq [ S ] — частоту S в массиве , Count [ S ] — сколько чисел больше или равных S находится в массиве. В этих обозначениях ответ может быть выражен как сумма способов [ S ] * Count [ S ] для каждого возможного S . Теперь, как найти Ways []: давайте построим два полинома: P = Freq [0] * X 0 + Freq [1] * X 1 + … + Freq [ VALMAX ] * X VALMAX Q = P 2 Теперь мы можем получить формулу 902 902 03 03 [ S ] = ( Coef [ S ] — Freq [ S /2]) / 2, если S четное Ways [ S ] = Coef [ S ] / 2, если S является нечетным , где Coef [ S ] = коэффициент x S в Q . Если S четное, из общего числа возможных пар мы должны вычесть те пары, которые используют один и тот же элемент. После этого разделите на 2, чтобы получить количество упорядоченных пар (в терминах i и j сверху) на сумму S (если вы не хотите, чтобы были только упорядоченные пары, вы должны пропустить деление на 2). Q можно получить с помощью БПФ в O ( VlogV ), где V — максимальная сумма двух элементов из массива, в нашем случае 10 6 (но я думаю, что мы можем считать V = 10 5 , потому что любая сумма больше 10 5 может образовывать только хорошие треугольники) Окончательная временная сложность составляет O ( T * ( VALMAXlogVALMAX + NlogN )) Я повторяю еще раз , Не знаю, работает ли 🙂 МОЕ ИССЛЕДОВАНИЕ Сейчас я студент первого курса Черкасского национального университета имени Богдана Хмельницкого.Вы знаете, поскольку я не черкасец, живу в студенческом общежитии. По правде говоря, я рад этому, так как люблю быть независимым. В общежитии я делю комнату с двумя другими девушками. Один из них из Городища. Ее зовут Хелен. Другая девушка из Новомиргорода, города Кировоградской области. Она украинка. Ее зовут Ирэн. На самом деле они не только мои соседи по комнате, но и мои хорошие друзья. Итак, в Черкасском университете обучаются студенты из разных областей. У нас очень красивый и уютный номер. К тому же он очень светлый, так как обращен на запад. Все мы рано встаем. Обычно мы встаем в 7 часов. После обычной утренней зарядки и душа завтракаем. Так как мы не любим опаздывать на занятия, мы стараемся приходить в университет незадолго до 9 часов. Обычно у нас лекции и семинары утром, а иногда и днем. После занятий мы обедаем в студенческой столовой. Это не займет у нас много времени.Затем я обычно гуляю по зданию университета. Мне нравится делать это самому. Это мое представление о хорошем отдыхе. После этого иду в читальный зал и просматриваю журналы и периодические издания. Во вторник и пятницу я также делаю домашнее задание по английскому в читальном зале. Я возвращаюсь в свою комнату в хостеле поздно вечером. В выходной, то есть в воскресенье, я обычно езжу в центр Черкасс. Здесь так много всего, что можно увидеть, и так много мест, куда можно пойти. Среди них старые и современные дома, концертный зал, различные музеи, красивые старинные постройки.Есть также прекрасные зеленые парки и стадионы. Сегодня воскресенье. Я хочу пойти в театр со своим парнем. Его зовут Игорь. Он милый мальчик, очень милый и умный. Он тоже студент. Он занимается физикой. На самом деле его родители тоже физики. Его отец занимается исследованиями в области атомной физики. Надеюсь, сегодня вечером мы получим билеты в театр. Если не получим билеты, можно пойти в кино. Есть несколько новых фильмов. Я должен сдать выпускные экзамены в декабре. Наш первый семестр длится с первого сентября по октябрь и ноябрь. В ноябре у нас есть кредитные тесты, и если мы их успешно сдадим, то сможем сдать экзамены. Экзамены обычно заканчиваются 24 -го числа -го декабря. Потом были свободны. ЧЕТЫРЕ ОСНОВНЫХ ОПЕРАЦИИ АРИФМЕТИКИ Мы не можем прожить ни дня без цифр. Цифры и цифры везде. На этой странице вы видите названия номеров.Это ноль, один, два, три, четыре и так далее. А вот цифры: 0, 1, 2, 3, 4 и так далее. В системе счисления числа используются для обозначения чисел, а числа сгруппированы особым образом. Числа, используемые в нашей системе счисления, называются цифрами. В нашей индуистско-арабской системе мы используем только десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 для обозначения любого числа. Мы снова и снова используем одни и те же десять цифр в системе счисления с основанием десять. Эти цифры могут использоваться в различных комбинациях.Таким образом, 1, 2 и 3 используются для записи, 123, 132, 213 и так далее. Одно и то же число могло быть представлено по-разному. Например, возьмите число 3. Его можно представить как 2 + 1, 4 — 1 и так далее. Очень простой способ сказать, что каждая из цифр называет одно и то же число, — это написать уравнение — математическое предложение, между которыми стоит знак равенства (=). Например, 3 + 4 = 5 + 2 или 3 1 = 6 — 4. + — это знак плюс. Знак — минус. Мы говорим, что три плюс шесть равно пяти плюс четыре, или три минус 1 равно шести минус четыре.Другой пример уравнения — 3 + 5 = 8. В этом уравнении тройка является добавлением. Пять — это тоже добавление. Восемь — это сумма. Складываем три и пять и получаем восемь. Есть четыре основных арифметических действия, о которых вы все знаете. Это сложение , вычитание , умножение и деление . В арифметике операция — это способ думать о двух числах и получать одно число. Как вы помните из вышеизложенного, в операции сложения два числа, с которыми вы работаете, называются слагаемыми или слагаемыми , а число, которое вы получаете в результате этой операции, равно сумме .В вычитании вы снова используете два числа. В уравнении 7-2 = 5 семь — это минус , а два — субстрагенд . В результате этой операции вы получите разницы . Мы можем сказать, что вычитание — это операция, обратная сложению, поскольку 5 + 2 = 7 и 7-2 = 5. То же самое можно сказать и о умножении и делении , которые также являются обратными операциями. В умножении есть число, которое нужно умножить.Это множимое . Также есть множитель . Если умножить множимое на множитель, мы получим , в результате получим произведение . Когда два или более числа умножаются, каждое из них называется множителем . Например, в выражении 5 x 2 (пять, умноженные на два) 5 и 2 будут множителями. Множаемое и множитель — это названия факторов. В операции деления есть число, которое делится, и оно называется делимым ; число, на которое мы делим, называется делителем .В результате операции деления получим частное . В некоторых случаях делитель не входит в делимое целое число раз. Например, если вы разделите 10 на 3, вы получите оставшуюся часть дивиденда. Эта часть называется , остальные . В нашем случае это будет 1. Так как умножение — это операция, обратная делению, вы можете проверить деление, используя умножение. При разделении необходимо помнить два очень важных факта. a) Частное равно 0, если делимое равно 0, а делитель не равен 0. То есть 0: n для всех значений n , кроме n = 0. б) Деление на 0 бессмысленно. Если вы говорите, что не можете делить на 0, это на самом деле означает, что деление на 0 бессмысленно. То есть n : 0 бессмысленно для всех значений n . БАЗОВЫЕ ДВА ЧИСЛА Во второй половине семнадцатого века великий немецкий философ и математик Готфрид Вильгельм фон Лейбниц (1646–1716) проводил исследования простейшей системы счисления.Он разработал систему счисления, в которой используются только символы 1 и 0. Эта система называется двоичной или двоичной системой счисления. Лейбниц фактически построил механическую вычислительную машину, которая до недавнего времени стояла бесполезной в музее в Германии. На самом деле он создал свои счетные машины примерно за три столетия до того, как их сделали современные производители машин. Двоичная система счисления, введенная Лейбницем, используется только в некоторых из самых сложных электронных вычислительных машин.Цифра 0 соответствует выключенному состоянию, а цифра 1 соответствует включению электрической цепи компьютера. Две цифры с основанием обозначают группы единиц, двоек, четверок, восьмерок и так далее. Разрядное значение каждой цифры в 1101 в основании ДВА, как показано вышеупомянутыми словами (вкл. Или выкл.), А также степенями 2 в обозначении ДЕСЯТЬ по основанию, как показано ниже. Число 1101 в основании ДВА означает, что один, умноженный на два в кубе, плюс один, умноженный на два в квадрате, плюс ноль, умноженный на два, плюс один, умноженный на единицу, равно (1X8) + (1×4) + (0X2) + (1×1) = 8 + 4 + 0 + 1 = 13.Следовательно, 1101 в базе ДВА = 13. Цифра с основанием десять может быть заменена на цифру с основанием два путем деления на степени двойки.Из вышесказанного вы знаете, что двоичная система счисления широко используется в высокоскоростных электронных компьютерах. Соответствие между двумя цифрами, используемыми в двоичной системе, и двумя положениями (включено и выключено) механического переключателя, используемого в электронной схеме, объясняет это широкое использование. Двоичная система исчисления представляет собой простейшую разрядную систему счисления. В каждой такой системе счисления должны быть символы для чисел 0 и 1. Мы использовали 0 и 1, потому что были хорошо знакомы с ними. СОБСТВЕННОСТЬ ЗАКРЫТИЯ Если мы сложим два натуральных числа, сумма также будет натуральным числом. Например, 5 — натуральное число, а 3 — натуральное число. 5 + 3 = 8 и только 8. Сумма 8 также является натуральным числом. Ниже приведены другие примеры, в которых складываются два натуральных числа, и сумма является другим натуральным числом. 19 + 4 = 23 и только 23; 6 + 6 = 12 и только 12; 1429 + 357 = 1786 и только 1786.На самом деле, если складываются любые два натуральных числа, сумма снова является натуральным числом. Поскольку это верно, мы говорим, что множество натуральных чисел замкнуто относительно сложения. Это заявление о замыкании, одно из особых свойств сложения. Обратите внимание, что мы можем назвать сумму в каждом из приведенных выше уравнений. То есть существует сумма 5 и 3, или, например, существует число, которое является суммой 19 и 4. Фактически существует сумма любых двух чисел. Это называется свойство существования .Также обратите внимание, что когда добавляются 5 и 3, получается 8, а только 8, а не какое-то другое число. Поскольку существует одна и только одна сумма для 19 + 4, мы говорим, что сумма уникальна. Это называется свойством уникальности . В определении закрытия подразумеваются как существование, так и уникальность. Если a и b являются числами данного набора, то a + b также является числом того же набора. Например, если a и b — любые два натуральных числа, то существует a + b , оно уникально и снова является натуральным числом. Если мы используем операцию вычитания вместо операции сложения, мы не сможем сделать заявление, которое мы сделали выше. Если одно натуральное число вычитается из другого натурального числа, результат иногда оказывается натуральным числом, а иногда — нет. 11-6 = 5, а 5 — натуральное число. 99 = 0 и 0 не является натуральным числом. Рассмотрим уравнение 4-7 = n. Это невозможно решить, если в качестве ответа нужно использовать натуральное число. Следовательно, множество натуральных чисел не замыкается при вычитании. Когда умножаются два натуральных числа, всегда получается натуральное число, которое является произведением двух чисел. Каждая пара натуральных чисел имеет уникальный продукт, который снова является натуральным числом. Таким образом, множество натуральных чисел замкнуто относительно умножения. В общем, свойство закрытия может быть определено следующим образом: если x и являются любыми элементами, не обязательно одинаковыми, набора A и * (звездочка) обозначает операцию *, то набор A закрывается при выполнении операции * если (x * y) является элементом множества A. Следует отметить, что невозможно найти сумму или произведение всех возможных пар натуральных чисел. Следовательно, мы принимаем свойство замыкания без доказательства, то есть как аксиому. ВСЕ НОМЕРА Многие математические утверждения связаны не с одним числом, а с набором чисел, которые имеют какое-то общее свойство. Например, такой набор чисел — это набор нечетных чисел 0, 2, 4, 6 или набор четных чисел 1, 3, 5, 7. Какое свойство является общим для всех четных чисел? Какое свойство является общим для всех нечетных чисел? Вы должны знать, что результат умножения называется произведением, а числа, которые нужно умножить, — множителями.Когда вы пишете 6X3 = 18, это означает, что вы записываете число 18 как произведение двух целочисленных множителей. Другая пара целочисленных множителей будет 9 и 2, так как 9X2 = 18. Сможете ли вы назвать другие множители 18? Поскольку 6X3 = 3X6, позвольте нам назвать 6 и 3 только одной парой множителей 18. Когда вы используете 0 как один из факторов, каким должен быть продукт? То есть какое число равно 0, умноженному на 5? Или 7 умножить на 0 равно какому числу? Ответы на эти вопросы резюмируются в следующем утверждении: Для любого оператора a , ax0 = 0 = xa .В некоторых случаях, когда нам нужно указать целое число в имени факториала, можно использовать более двух факторов. Мы можем, например, назвать 60 как произведение трех факторов. Поскольку умножение ассоциативно, мы знаем, что (3X4) X5 = 3X4X5 = 3X (4X5). Мы также можем написать 60 = 3X4X5; 60 = 3X5X4 и так далее. Поскольку aX1 = a для любого числа a , мы знаем, что 1 является множителем каждого целого числа. Согласимся опустить 1 как фактор при именовании числа в факторизованной форме. В каждом из приведенных выше уравнений используется один и тот же набор множителей, а именно 3, 4 и 5. Независимо от порядка, в котором они написаны, 3, 4 и 5 следует рассматривать как один набор из трех множителей 60. Также 60 можно записать как произведение четырех факторов, как показано в уравнении 60 = 3X2X2X5. В предыдущих упражнениях вы, вероятно, заметили, что некоторые факторы, которые вы использовали, могут быть учтены дальше, а другие — нет. В уравнении 18 = 6X3 коэффициент 6, в свою очередь, можно записать как 3X2.Если вы сделаете это, вы получите 18 = 2X3X3. Ни один из этих трех факторов не может быть записан в фактической форме, если вы не используете 1 в качестве фактора. Следовательно, 2X2X3 — это форма, содержащая наименьшие множители 18. Вы можете сделать то же самое с нечетным числом, скажем 105, где 105 = 3X35 = 3X5X7. Вы уже знаете, что каждое целое число имеет 1 и само себя как фактор. То есть 9X1 = 9 и 11X1 = 11. Некоторые такие числа имеют только 1 и сами по себе как фактор. Поскольку его единственные множители — 1 и 5, таким числом является 5. Целое число называется простым числом или просто простым, если: а) Больше 1. б) Его единственные множители — 1 и он сам. Любое целое число, кроме 0 и 1, которое не является простым числом, называется составным числом или просто составным числом. Подсчитайте количество возможных треугольников с учетом набора палочек
ЧЕТЫРЕ ОСНОВНЫХ ОПЕРАЦИИ АРИФМЕТИКИ
два в кубе два в квадрате два в первой степени Восьмерки Четверки двое Единицы :





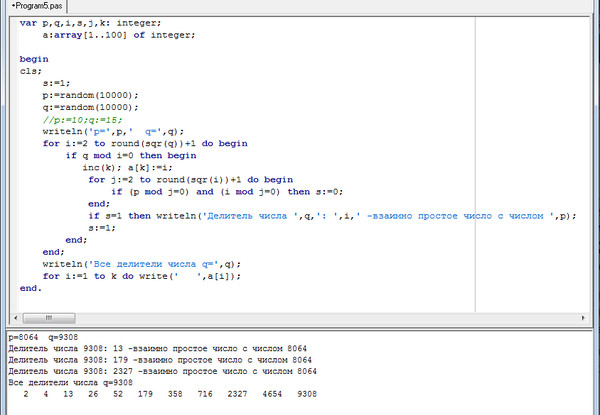 Составляем число с переставленными цифрами справа налево: }
N := 100 * (N div 10 mod 10) + 10 * (N div 100) + N mod 10;
writeln('Две первые цифры меняем местами: ', N);
readln
end.
Составляем число с переставленными цифрами справа налево: }
N := 100 * (N div 10 mod 10) + 10 * (N div 100) + N mod 10;
writeln('Две первые цифры меняем местами: ', N);
readln
end.
Leave a Reply