Задачи на числа: Задачки с числами – Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Задачки с числами

Загаданные учителем числа были 2 и 9. Ниже приведена вся логическая цепочка рассуждений. (Примечание: Если приведённое ниже решение кажется Вам не совсем понятным, то чуть ниже Вы найдёте более детальный анализ логоритма решения задачи на примере двух числовых комбинаций.)

Итак, необходимо определить два натуральных числа больше 1(единицы). Первый студент знает их произведение, а второму известна их сумма. Нам известно, что сумма задуманных чисел меньше 14 , поэтому рассмотрим следующие варианты:

2 2 – НЕТ – иначе первый студент тоже знал бы их сумму…
2 3 – НЕТ – иначе первый студент тоже знал бы их сумму…
2 4 – НЕТ – иначе первый студент тоже знал бы их сумму…
2 5 – НЕТ – иначе первый студент тоже знал бы их сумму…
2 6
2 7 – НЕТ – иначе первый студент тоже знал бы их сумму…
2 8

2 9
2 10
2 11 – НЕТ – иначе первый студент тоже знал бы их сумму…
3 3 – НЕТ – иначе первый студент тоже знал бы их сумму…
3 4
3 5 — – НЕТ – иначе первый студент тоже знал бы их сумму…
3 6
3 7 – НЕТ – иначе первый студент тоже знал бы их сумму…
3 8 – НЕТ – произведение этих чисел не дает таких вариантов, чтобы все другие возможные множетели, дающее то же произведение, в сумме были меньше 14 (например, 2+12).
3 9 – НЕТ – иначе первый студент тоже знал бы их сумму…
3 10 – НЕТ – произведение этих чисел не дает таких вариантов, чтобы все другие возможные множетели, дающее то же произведение, в сумме были меньше 14.
4 4
4 5
4 6 – НЕТ – произведение этих чисел не дает таких вариантов, чтобы все другие возможные множетели, дающее то же произведение, в сумме были меньше 14.
4 7 – НЕТ – произведение этих чисел не дает таких вариантов, чтобы все другие возможные множетели, дающее то же произведение, в сумме были меньше 14.
4 8 – НЕТ – произведение этих чисел не дает таких вариантов, чтобы все другие возможные множетели, дающее то же произведение, в сумме были меньше 14.
4 9 – НЕТ – произведение этих чисел не дает таких вариантов, чтобы все другие возможные множетели, дающее то же произведение, в сумме были меньше 14.
5 5 – НЕТ – иначе первый студент тоже знал бы их сумму…
5 6 – НЕТ – произведение этих чисел не дает таких вариантов, чтобы все другие возможные множетели, дающее то же произведение, в сумме были меньше 14.
5 7 – НЕТ – иначе первый студент тоже знал бы их сумму…
5 8 – НЕТ – произведение этих чисел не дает таких вариантов, чтобы все другие возможные множетели, дающее то же произведение, в сумме были меньше 14.
6 6 – НЕТ – произведение этих чисел не дает таких вариантов, чтобы все другие возможные множетели, дающее то же произведение, в сумме были меньше 14.
6 7 – НЕТ – произведение этих чисел не дает таких вариантов, чтобы все другие возможные множетели, дающее то же произведение, в сумме были меньше 14.
Итак, остаются следующие вероятные комбинации, которые рассмотрим более подробно:
2 6 – НЕТ – для суммы этих двух чисел невозможно подобрать другие слагаемые, дающие тот же результат (8), чтобы перемножив эти слагаемые (например, 4х4), Вы получили бы произведение (16), другие возможные множители которого в сумме дают больше 14 (например, 2+8= 10).
2 8
2 9
2 10
3 4 – НЕТ – для суммы этих двух чисел невозможно подобрать другие слагаемые, дающие тот же результат, чтобы перемножив эти слагаемые, Вы получили бы произведение, другие возможные множители которого в сумме дают больше 14.
3 6 – НЕТ – для суммы этих двух чисел невозможно подобрать другие слагаемые, дающие тот же результат, чтобы перемножив эти слагаемые, Вы получили бы произведение, другие возможные множители которого в сумме дают больше 14.
4 4 – НЕТ – для суммы этих двух чисел невозможно подобрать другие слагаемые, дающие тот же результат, чтобы перемножив эти слагаемые, Вы получили бы произведение, другие возможные множители которого в сумме дают больше 14.
4 5 – НЕТ – для суммы этих двух чисел невозможно подобрать другие слагаемые, дающие тот же результат, чтобы перемножив эти слагаемые, Вы получили бы произведение, другие возможные множители которого в сумме дают больше 14.
Второй студент (которому была известна сумма загаданных чисел) знал, что первому студенту (которому было известно произведение загаданных чисел) неизвестна сумма чисел, и думал, что первому студенту неизвестно, что сумма чисел меньше 14.

Остаются только три вероятные комбинации:
2 8 – произведение =16, сумма =10
2 9 – произведение=18, сумма=11
2 10 – произведение=20, сумма=12

Отбросим суммы, которые образуются путем сложения уникальных комбинаций чисел – если известно такое произведение чисел, при котором сумма очевидна (мы могли бы и гораздо раньше оговорить этот момент, но тогда потерялась бы вся прелесть головоломки) – потому что второй студент знал, что известная ему сумма точно не из этой комбинации чисел. Таким образом, сумма не может быть равна 10 (из-за 7 и 3, при которых произведение 21 явно выдаст эти числа). Второй студент знает, что первому студенту сумма неизвестна, но если бы сумма была бы равна 10, то первый студент знал бы сумму, если бы комбинация чисел была 7 и 3. Аналогичным способом отбрасываем сумму 12 (из-за 5 и 7, при умножении выдающие себя в уникальном произведении 35).

И остается только один вариант – числа 2 и 9. Задача решена.

Если приведённое выше решение кажется Вам не совсем понятным, то сейчас мы разберм более детально основной логоритм решения задачи на примере двух числовых комбинаций.

Возьмём числа 6 и 2 и посмотрим, сработает ли такая комбинация.

Первому студент известно произведение, а второму известна сумма этих чисел.
Значит, первому известно произведение 12, а второму – сумма 8.

Первый: «Я не знаю сумму.»
Известное мне произведение равно 12, а получить такое произведение можно так: либо 6х2, либо 3х4. Значит, второму известна сумма, равная либо 8, либо 7.

Второй: «Я знал, что ты не знаешь. Сумма меньше 14.»
Известная мне сумма равна 8, а получить такую сумму можно, сложив 6+2, 5+3 или 4+4. Первый вариант слагаемых даст произведение 12, второй – 15, третий – 16.

Произведение, равное 15 можно сразу вычеркнуть (то есть вариант с числами 5 и 3 отбросить), потому что 15-число уникальное – его можно получить исключительно через натуральные числа 5 и 3, так что будь это именно такая комбинация чисел, студенту были бы известны и произведение, и сумма с самого начала.

Рассмотрим произведение 16. Его можно получить, если множители – либо 4х4, либо 8х2. В этом случае фраза, что сумма этих множителей представляла бы собой число <14, другому студенту никак не поможет (4+4 и 8+2 <14).

Рассмотрим произведение 12. В этом случае студент будет рассчитывать на то, что возможные комбинации чисел – это 4х3 или 6х2. Но и в этом случае фраза, что сумма этих множителей представляла бы собой число <14, другому студенту никак не поможет (4+3 и 6+2 <14).

Следовательно, невозможно подобрать такую комбинацию чисел, составляющих в сумме число 8, где другие слагаемые, дающие ту же сумму, если их перемножить, дадут произведение, другие возможные множители которого в сумме дают больше 14. Например, если это 4 и 4, то нет такой суммы из возможных других множетелей произведения 4х4, которые в сумме дали бы число больше 14 (2+8=10).

Первый: «Теперь я знаю эти числа.»
Я не знал, то ли это 6х2, то ли это 3х4, а второй студент говорит мне, что сумма меньше 14. Но это абсолютно очевидно, что он подумал, что из суммы, равной 8 или 7, можно найти такой вариант слагаемых, произведение которых послужит суммой, которая должна быть больше 14.
Но мне его слова абсолютно не помогли, потому что 6+2 и 3+4 в любом случае меньше 14. Таким образом, комбинация чисел 6 и 2 неверна.

Теперь возьмём числа 9 и 2 и посмотрим, подходит ли такая комбинация.

Первому студент известно произведение, а второму известна сумма этих чисел.
Значит, первому известно произведение 18, а второму – сумма 11.

Первый: «Я не знаю сумму.»
Известное мне произведение равно 18, а получить такое произведение можно так: 9х2 или 6х3. Значит, второму известна сумма, равная либо 11, либо 9.

Второй: «Я знал, что ты не знаешь. Сумма меньше 14.»
Известная мне сумма равна 11, а получить такую сумму можно, сложив 9+2, 8+3, 7+4 или 6+5. Первый вариант слагаемых даст произведение 18, второй – 24, третий – 28, четвёртый – 30.

Если первому студенту известно произведение, равное 18, то он будет рассматривать варианты комбинаций: 9х2 и 6х3, поэтому если я скажу ему, что сумма должна быть меньше 14, это подскажет ему, что у меня есть и другая вероятность, при которой сумма будет больше либо равна 14. Так оно и есть (см три следующих абзаца): 12+2, 14+2 и 15+2.

Если первому студенту известно произведение, равное 24, то он будет рассматривать варианты комбинаций 6х4, 8х3 и 12х2, но 12+2 – это уже 14, так что если произведение, известное первому студенту, было бы 24, то он не мог бы быть абсолютно уверен, что сумма будет меньше 14.

Если первому студенту известно произведение, равное 28, то он будет рассматривать варианты комбинаций 7х4 или 14х2, но 14+2=16, так что если произведение, известное первому студенту, было бы 28, то он не мог бы быть абсолютно уверен, что сумма будет меньше 14.

Если первому студенту известно произведение, равное 30, то он будет рассмтривать варианты комбинаций 5х6, 10х3 и 15х2, но 15+2=17, так что если произведение, известное первому студенту, было бы 30, то он не мог бы быть абсолютно уверен, что сумма будет меньше 14.

Первый: «Теперь я знаю эти числа.»
Я не знал, то ли это 9х2, то ли это 6х3, а второй студент говорит мне, что сумма меньше 14. Должно быть, у него были варианты с суммой ≥14, но это невозможно для суммы 9, полученной с помощью комбинации из 6 и 3. Следовательно, известная ему сумма равна 11, и получена она путем сложения 9 и 2.

Задачи с целыми числами

Задачи эти предлагались репетиторам на сертификации по математике портала “Профи.ру”. Задачи не очень сложные, их уровень вполне соответствует 19 задаче ЕГЭ, но интересные.

Задача 1. Чему равно наименьшее восьмизначное число, дающее при делении на 297 остаток 289, при делении на 61 остаток 53, при делении на 21 остаток 13, при делении на 45 остаток 37, при делении на 826 остаток 818?

Решение: обозначим искомое число . Тогда

   

Глядя на это выражение, становится понятно, что решение затянется… Но можно заметить, что указанное выше выражение можно записать и так:

   

Тогда становится понятно, что нужно найти наименьшее общее кратное чисел 297, 61, 21, 45 и 826.

   

   

   

   

61 – простое число. Следовательно,

   

Ответ: .

Задача 2. Дату 9 октября 1963 года можно записать тремя числами: 9.10.63, которые оказались расположены в порядке неубывания. Во все дни, когда соответствующие три числа располагались в порядке неубывания, на металлообрабатывающем заводе проводились заседания. Чему равно количество дней, которые были посвящены заседаниям, если завод работал с 24 января 1957 года по 6 декабря 2004 года, а даты открытия и закрытия также учитываются?

Начинаем считать. В 57 году было проведено заседаний: 2 в феврале, 3 в марте, 4 в апреле и так далее, 12 в декабре. Итого (сумма прогрессии):

   

Итак, всего 77 заседаний – так как в январе завод еще не был открыт.

С 58 по 99 год, таким образом, проводилось по 78 заседаний – еще одно в январе.

В 2000 году заседаний не было. В 2001 – только 1, 1 января.

В 2002 – три, одно в январе и 2 в феврале.

В 2003 – 6 (в январе, феврале и марте), в 2004 – 10 (в январе, феврале, марте и апреле).

Осталось сложить:

   

Ответ: 3373.

Задача 3. Число 1447243 написали 45 раз подряд, при этом получилось 315-значное число. Из этого числа требуется вычеркнуть 3 цифры. Сколькими способами это можно сделать, если полученное 312-значное число должно делиться на 6?

Так как число 6 делится на два и на три, то полученное 312-значное число обязано быть четным. Поэтому последнюю тройку надо вычеркивать. Далее, так как число 1447243 написали 45 раз подряд, то даже без последней тройки оно делится на 3. Поэтому две вычеркнутые нами цифры в сумме обязаны делиться на три. Это 7 и 2  или 2 и 4, или 1 и 2 – никакие две другие в сумме не дадут кратную трем сумму. При этом последнюю в записи 312-значного числа 4 тоже можно вычеркнуть, но нельзя вычеркнуть сразу и 2 и 4, идущие последними. Имеем 135 четверок, 45 семерок, 45 единиц  и 45 двоек – двойку вычеркнуть обязательно. Поэтому у нас 45 способов это сделать. После этого у нас 45 способов вычеркнуть 7 – итого 2025 способов. Также 45 способов вычеркнуть 1 – это еще 2025 способов.Если вместе с двойкой вычеркиваем четверку –  то у нас 134 способа – последнюю нельзя. Итого 6030 способов. Всего 10080 способов.

Ответ: 10080.

Задача 4. Чему равно наибольшее количество цифр, стертых в 1740-значном числе , если сумма оставшихся цифр равна 1808?

Заметим, что часть 8633 составляет «период» данного числа. Эта часть состоит из 4 цифр, следовательно, в числе она повторяется раз. Сумма цифр этой части равна 20, следовательно, общая сумма всех цифр числа равна . Раз осталась сумма 1808 – следовательно, сумма вычеркнутых равна . Так как требуется вычеркнуть наибольшее количество цифр, то будем вычеркивать сначала все тройки. Сумма всех троек в числе равна . Теперь, если вычеркнуть все шестерки – это дает еще 2610. Остается вычеркнуть еще какое-то количество восьмерок. Определим, сколько:

   

   

Итого, мы вычеркнули 870 троек, 435 шестерок и 209 восьмерок – всего 1514 цифр.

 

Задача 5. Число 5081500199 написали 37 раз подряд, при этом получилось 370-значное число. Из этого 370-значного числа требуется вычеркнуть 5 цифр. Чему равно количество способов, которыми это можно сделать, если полученное после вычеркивания 365-значное число должно делиться на 30?

Так как 30 делится на 5, на 2  и на 3, то придется обязательно вычеркивать три последние цифры – 199. Остается вычеркнуть еще 2. Сумма цифр числа 5081500199 – 38 – не делится на три, число 37 – также. Поэтому надо вычеркивать такие цифры, чтобы добиться делимости на три.  После вычеркивания последних трех цифр (199) мы также не добились того, чтобы число делилось на три.

Сумма цифр числа после вычеркивания 199 составляет 1387.

Чтобы добиться делимости на три, нужно вычеркивать либо две пятерки (1377 делится на 3), либо 1 и 0 (1386), либо 8 и 5 (1374) – эти суммы «заберут» лишнюю  единицу, и число будет делиться на три. При вычеркивании ноля может быть вычеркнут и последний – это не изменит четности и делимости на 5. Итак, считаем. У нас 74 пятерки, то есть первую можно вычеркнуть 74 способами. Вторую – уже 73. Следовательно, способов вычеркнуть две пятерки – . Вторая пара: единицу можем выбрать 73 способами (одна зачеркнута в самом начале), 0 – 111 способами. Следовательно, вторую пару можно выбрать способами.

Способов выбрать восьмерку – 37, пятерку – 74. Поэтому эта пара даст способов. Итого способа.

Ответ: 16243 способа.

 

4 детские задачки, которые решат не все взрослые

Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте

Иногда детишкам задают такие задачи, над которыми половина офиса может зависнуть, забыв о работе. А малыши решают их с ходу.

AdMe.ru предлагает 4 совсем детские задачки. Попробуйте решить.

Задача № 1. Парковка

Это простой вопрос из гонконгского теста для зачисления в начальную школу.

Ответ: 87.
Надо просто мысленно повернуть картинку вверх ногами.

Задача № 2. Четырехзначные числа

Дошколята решают эту задачку за 5-10 минут. Программисты — за 1 час.

Ответ: 2581 = 2.
В каждой группе из 4 чисел нужно было всего лишь сосчитать замкнутые кружочки. Например, у цифры 6 один кружочек, у цифры 8 — два. А, значит, у числа 6889 их шесть. И так далее.

Задача № 3. Числовая пирамида

Задачки, как эта, сингапурские третьеклассники щелкают как орешки.

Ответ: D = 1345; E = 2440.
Первым делом складываете два числа в нижнем ряду: 198 + 263 = 461.
Получилась сумма больше того числа, что стоит над ними: 461 > 446.
Вычитаете из большего меньшее: 461 — 446 = 15.
Точно так же считаем остальные пары и видим, что везде получается 15.
Та-дам! Вот и ключ к решению.

Задача № 4. Шоколадная коробка

Задачка из США для детей 12-13 лет: «В коробке 50 шоколадок. Из них 30 с карамелью, 25 — с кокосом, 10 — и с карамелью, и с кокосом, а остальные вообще без начинки.

Вопрос: Какая диаграмма верно отражает содержимое коробки?».

Ответ: диаграмма B.
Простая арифметика:
Сколько шоколадок только с карамелью? 30 — 10 = 20.
Сколько шоколадок только с кокосом? 25 — 10 = 15.
Сколько же остается шоколадок без начинки? 50 — (20 + 15 +10) = 5.

Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте

Задачи на целые числа

Задачи на целые числа.

Э.С.Минхаерова, учитель математики МБОУ СОШ №5 с углубленным изучением отдельных предметов, г.Бугульма, РТ

Вы можете с каждым днём становиться

всё умнее и умнее. Ум может

развиваться – его можно, укрепить,

настроить и подготовить так, что он

будет творить чудеса.

Мэрилин вос Сэйвэнт

Мозг человека уникален, такого мозга, как у нас, нет ни у кого. И он требует постоянной, систематической тренировки. Математика предоставляет для этого широкие возможности.

Задачи на целые числа всегда считались одними из наиболее сложных задач. Для их решения необходимо умение логически мыслить, охватывать всю задачу целиком, как говорят шахматисты, «просчитывать на несколько ходов вперед». Математических знаний для решения задач данного типа нередко хватает и пятикласснику, но подводит неготовность разбираться в ситуации. Вот это качество и необходимо развивать в детях.

Начиная с 5 класса я предлагаю своим ученикам задачи нестандартного типа, в частности задачи на целые числа. Пятиклассники справляются с задачами на свойства четных и нечетных чисел.

Пример 1. Петя купил общую тетрадь объемом 96 листов и пронумеровал все ее страницы по порядку числами от 1 до 192. Вася вырвал из этой тетради 25 листов и сложил все 50 чисел, которые на них написаны. Могло ли у него получиться 1990?

Решение: на каждом листе сумма номеров страниц нечетна, а сумма 25 нечетных чисел — нечетна.

Пример 2. Кузнечик прыгает по прямой, причем в первый раз он прыгнул на 1 см в какую-то сторону, во второй раз – на 2 см и так далее. Докажите, что после 1985 прыжков он не может оказаться там, где начинал.

Решение: сумма 1 + 2 + … + 1985 нечетна.

Пример 3. В народной дружине 100 человек и каждый вечер трое из них идут на дежурство. Может ли через некоторое время оказаться так, что каждый с каждым дежурил ровно один раз?

Решение: так как на каждом дежурстве, в котором участвует данный человек, он дежурит с двумя другими, то всех остальных можно разбить на пары. Однако 99 – нечетное число.

Пример 4. Есть 101 монета, из которых 50 фальшивых, отличающихся по весу на 1 грамм от настоящих. Петя взял одну монету и за одно взвешивание на весах со стрелкой, показывающей разность весов на чашках, хочет определить фальшивая ли она. Сможет ли он это сделать?

Решение: нужно отложить данную монету в сторону, а затем разделить остальные 100 монет на две кучки по 50 монет, и сравнить веса этих кучек. Если они отличаются на четное число грамм, то интересующая нас монета настоящая. Если же разность весов нечетна, то монета фальшивая.

В 6 классе можно добавить задачи на делимость, изучив при этом свойства и признаки делимости.

Пример 5. Винни-Пуху подарили 40 конфет. Он съел сколько влезло, а остальными хотел угостить поровну трех гостей. Но тут пришел четвертый гость. Пришлось хозяину съесть еще 3 конфеты, чтобы число оставшихся делилось на 4. Когда пришел пятый гость, пришлось съесть еще 3 конфеты, чтобы число оставшихся делилось на 5. и тут пришёл шестой гость. сколько конфет придётся съесть на этот раз, чтобы оставшиеся поделить поровну на шестерых.

Решение: пусть х- конфет осталось когда пришел шестой гость, тогда х+4 осталось когда пришел 5 гость. Так как по условию х+4 делится на 4, тогда и х делится на 4,но по условию х делится еще и на 5, значит, НОК равен 20. Если 20 поделить на 6 то в остатке останется 2, следовательно, Винни нужно съесть две конфеты.

Пример 6. Докажите что среди 18 идущих подряд трехзначных чисел найдется число, которое делится на свою сумму цифр.

Решение: среди подряд 18 идущих чисел найдется число N которое делится на сумму своих цифр. 18 =2*9, значит в трехзначном числе 9+9+9=27, сумма цифр не должна превышать 27. Например, число 999 не делится на сумму своих цифр так как оно нечетное. Число N делится на сумму своих цифр, когда их сумма составляет или 9 или 18.

Пример 7. Могут ли числа 1234567897 и 1234567892 быть квадратами каких-либо целых чисел?

Решение: данные числа не могут являться квадратами целых чисел из-за своих последних цифр 7 и 2. Дело в том, что при возведении в квадрат целого числа, последняя цифра может быть равной 1, 4, 9, 6, 5, 0.

Ученики 7 класса решают задачи на делимость, четность и нечетность более высокого уровня сложности.

Пример 8. Найдите все такие наборы целых чисел (a, b, c ), для которых (3a-b)(3b-c)(3c-a)=15015

Решение:(3a-b)(3b-c)(3c-a)=15015

15015=5*3*11*7*13

3*3*3 (a-b/3)(b-c/3)(c-a/3)=15015

3*3(a-b/3)(b-c/3)(c-a/3)=5005

(3a-b)(3b-c)(c-a/3)=5005

3*a-b, 3*a-c, 3*c-a- нечет.

Чет.-нечет.=нечет.

a,b,c-не могут быть четными

a,b,c -не могут быть нечетными, следовательно задача не имеет решения.

Пример 9. Числа m и n целые. Какова четность числа mn(m+n)?

Решение: переберем все возможные варианты четностей для чисел m и n. Их четыре, но в силу перестановочности достаточно рассмотреть лишь три: 1) Ч^.Ч(Ч+Ч)=Ч^.Ч=Ч; 2) Ч^.Н(Ч+Н)=Ч^.Н=Ч; 3) Н^.Н(Н+Н)=Н^.Ч=Ч. Следовательно, во всех случаях получаем четное число.

Пример 10. доказать, что число 2¹⁷ + 7¹⁸ + 9¹⁹ делится на 10.

Решение: Рассмотрим равенство 2¹⁷ = 2^{4 .} 2^{4 .} 2^{4 .} 2^{4 .} 2. Число 2⁴ имеет последней цифрой 6 ( 2⁴ = 16 ). Тогда число 2^{4 .} 2^{4 .} 2^{4 .} 2⁴ также заканчивается цифрой 6. В итоге получаем, что число 2¹⁷ заканчивается цифрой 2. Число 7¹⁸ представим в виде 7^{4 .} 7^{4 .} 7^{4 .} 7^{4 .} 7² . Число 7⁴ заканчивается цифрой 1 (7⁴ = 2401), тогда число 7^{4 .} 7^{4 .} 7^{4 .} 7⁴ также заканчивается цифрой 1. И, умножив 1 на 7² , получаем, что последняя цифра в числе 7^{4 .} 7^{4 .} 7^{4 .} 7^{4 .} 7² будет 9. Найдем последнюю цифру числа 9¹⁹ . Из равенств 9¹⁹ = 9^{2 .} 9^{2 .} 9^{2 .} 9^{2 .} 9^{2 .} 9^{2 .} 9^{2 .} 9^{2 .} 9^{2 .} 9 и 9² = 81 следует, что последняя цифра числа 9¹⁹ будет 9. Теперь очевидно, что сумма трех чисел, одно из которых заканчивается на 2, а два других заканчиваются на 9, делится на 10, так как последняя цифра равна 0.

Семиклассники могут справиться с решением диофантовых уравнений первого порядка.

Пример 11. В аквариуме живут осьминоги и морские звёзды. У осьминогов по 8 ног, а у морских звёзд – по 5. Всего конечностей насчитывается 39. Сколько в аквариуме животных?

Решение: заметим, что количество животных не может выражаться нецелым или отрицательным числами. Следовательно, если х – целое неотрицательное число, то и у=(39 – 5х)/8 должно быть целым и неотрицательным, а, значит, нужно, чтобы выражение 39 – 5х без остатка делилось на 8. Простой перебор вариантов показывает, что это возможно только при х = 3, тогда у = 3.

Пример 12. Андрей работает летом в кафе. За каждый час ему платят 10 р. И высчитывают 2 р. за каждую разбитую тарелку. На прошедшей неделе он заработал 180 р. Определите, сколько часов он работал и сколько разбил тарелок, если известно, что он работает не более 3 ч в день.

Решение: пусть x часов он всего работал в неделю, тогда 10х р. ему заплатили, но он разбил y тарелок, и с него вычли 2у р. Имеем уравнение 10х – 2у =180, причем x меньше или равен 21. Получим: 5х-у=90, 5х=90+у.

5х-у=90

5х= 90+у

1) у=5k 90+5k

у=5 х=19; у=10, х=20; у=15, х=21

В 8,9 классе задачи усложняются введением в них уравнений высших степеней, арифметической и геометрической прогрессий.

Пример 12. Найти все натуральные n, при которых число n²+5n+16 делится нацело на 169.

Решение: если данное число n²+5n+16 = (n+9)(n-4)+52 делится на 169=13², то оно делится и на 13. Так как число 52 делится на 13, то и произведение (n+9)(n-4) также делится на 13. Поэтому хотя бы один из его сомножителей n+9 или n-4 делится на 13, а так как (n+9) – (n-4) = 13, то сразу оба числа n+9 и n-4 делится на 13. Следовательно, их произведение делится на 169, а поскольку 52 не делится на 169, то сумма (n+9)(n-4)+52 не делится на 169. Итак, таких чисел нет.

Пример 13. Могут ли числа 2, 3, 5 быть членами одной геометрической прогрессии?

Решение: пусть q этой прогрессии, тогда 3 = 2qⁿ, 5 = 3q^m для некоторых n, m. Тогда qⁿ = 3/2, q^m = 5/3. Отсюда (3/2)^m = q^mn = (5/3)ⁿ , или 3^m / 2^m = 5ⁿ / 3ⁿ . Откуда 3^m+n = 2^{m .} 5ⁿ. Слева стоит нечетное число, а справа чётное, если только m не равен 0. Следовательно m=0. Но это тоже невозможно, так как в этом случае было бы 5 = 3q^m = 3^. 1=3. Полученное противоречие показывает, что требования 3 = 2qⁿ, 5 = 3q^m несовместимы. Следовательно числа 2, 3, 5 не могут быть членами одной геометрической прогрессии.

Пример 14. Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 10 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 150 метрам.

Решение: сумма прогрессии равна 150. Сумма первого и последнего членов – 10. Зная это, можем найти, какое количество дней улитка затратила на свой путь (количество членов прогрессии):

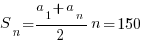
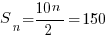
Откуда 

Таким образом, систематическое решение задач на целые числа повышает интерес учащихся к предмету, развивает умение разбираться в нестандартных ситуациях, способствует развитию логического мышления.

Литература.

1. Алфутова Н.Б., Устинов А.В. Алгебра и теория чисел. Сборник задач для математических школ. – М.:МЦНМО, 2002

2. Садовничий Ю.В. Математика. Задание 19. Решение задач и уравнений в целых числах – М.: Экзамен, 2017

3. Шаповалов А.В., Ященко И.В. Вертикальная математика для всех. Готовимся к задаче С: ЕГЭ с 6 класса – М.:МЦНМО, 2014

«Задачи на подсчет числа размещений, перестановок, сочетаний»

Урок ________

Тема программы: Комбинаторика

Тема: «Задачи на подсчет числа размещений, перестановок, сочетаний».

Цели:

— повторить формулы для нахождения числа различных видов комбинаций: размещений, перестановок, сочетаний без повторов; изучить формулы для нахождения числа различных видов комбинаций: размещений, перестановок, сочетаний с повторами, научиться распознавать задачи на нахождение размещений, перестановок, сочетаний; решить простейшие комбинаторные задачи с помощью этих формул;

— развивать познавательный интерес студентов, логическое мышление, умение применять знания в изменённой ситуации, делать выводы и обобщения; развивать  умения сравнивать, систематизировать, обобщать;

— формировать научное мировоззрение у обучающихся,  культуру математической речи,  информационную и  коммуникативную культуру студентов; воспитание дружелюбного отношения друг другу, умение работать в коллективе.

Оборудование:

Ход урока

I. Организационный момент

Преподаватель проверяет готовность к уроку.

Я рада приветствовать всех Вас на сегодняшнем уроке.

II. Мотивация. Сообщение темы, целей урока

1. Вопросы:

1. Определения: перестановки, размещения, сочетания.

2. Важен ли порядок? В каких соединениях? (размещение)

2. Решение задач:

№1. Экзамен состоит из 5 задач, которые можно решать в любом порядке. Сколькими способами можно расставить задачи. (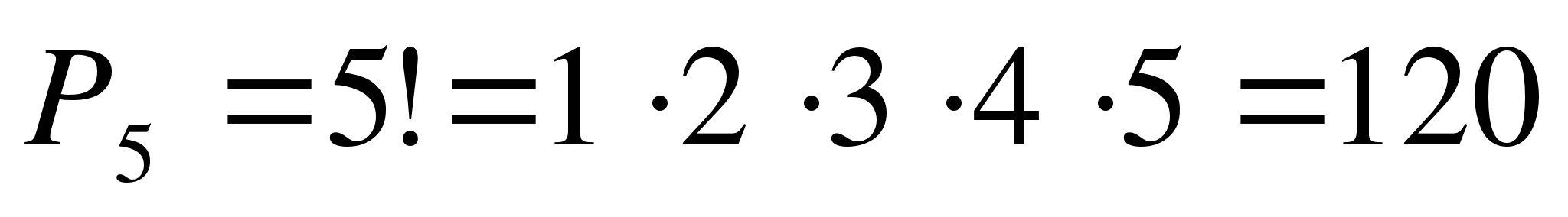способов)

№2. В магазине продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора. (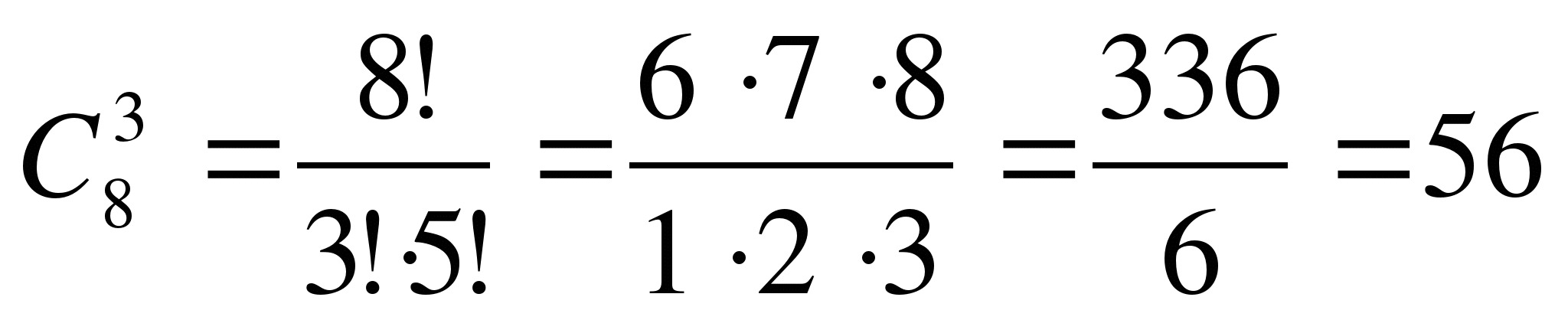способа)

№3. Сколько четырехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр 0, 2, 4, 6, 8. (всего чисел А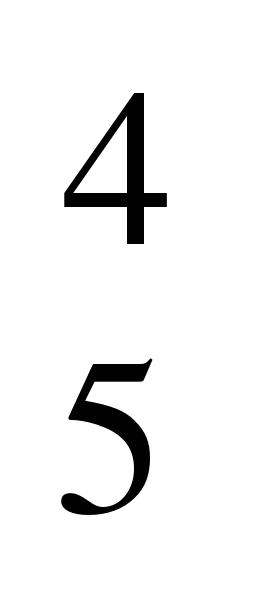, а чисел начинающихся с нуля —, тогда А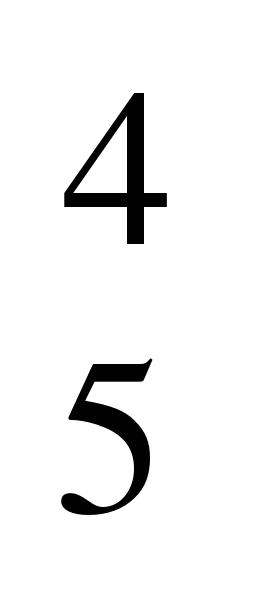—=96)

Тема сегодняшнего урока «Задачи на подсчет числа размещений, перестановок, сочетаний.». Давайте вместе попробуем сформулировать цели урока:

— научиться распознавать задачи на нахождение размещений, перестановок, сочетаний;

— решать простейшие комбинаторные задачи с помощью этих формул.

III. Изучение новой темы

1. Перестановка

Рассмотрим слово «КВАНТ», состоящее из 5 различных букв. Если менять порядок букв, получим 5!=120 перестановок

Если проделать то же самое со словом «АТАКА», то перестановок будет меньше, потому что, меняя местами 1,3 и 5-ю буквы, будем получать то же самое слово. Т.к. три буквы А можно менять местами 3!=6 способами, то перестановок будет в слове «АТАКА» в 6 раз меньше, т.е.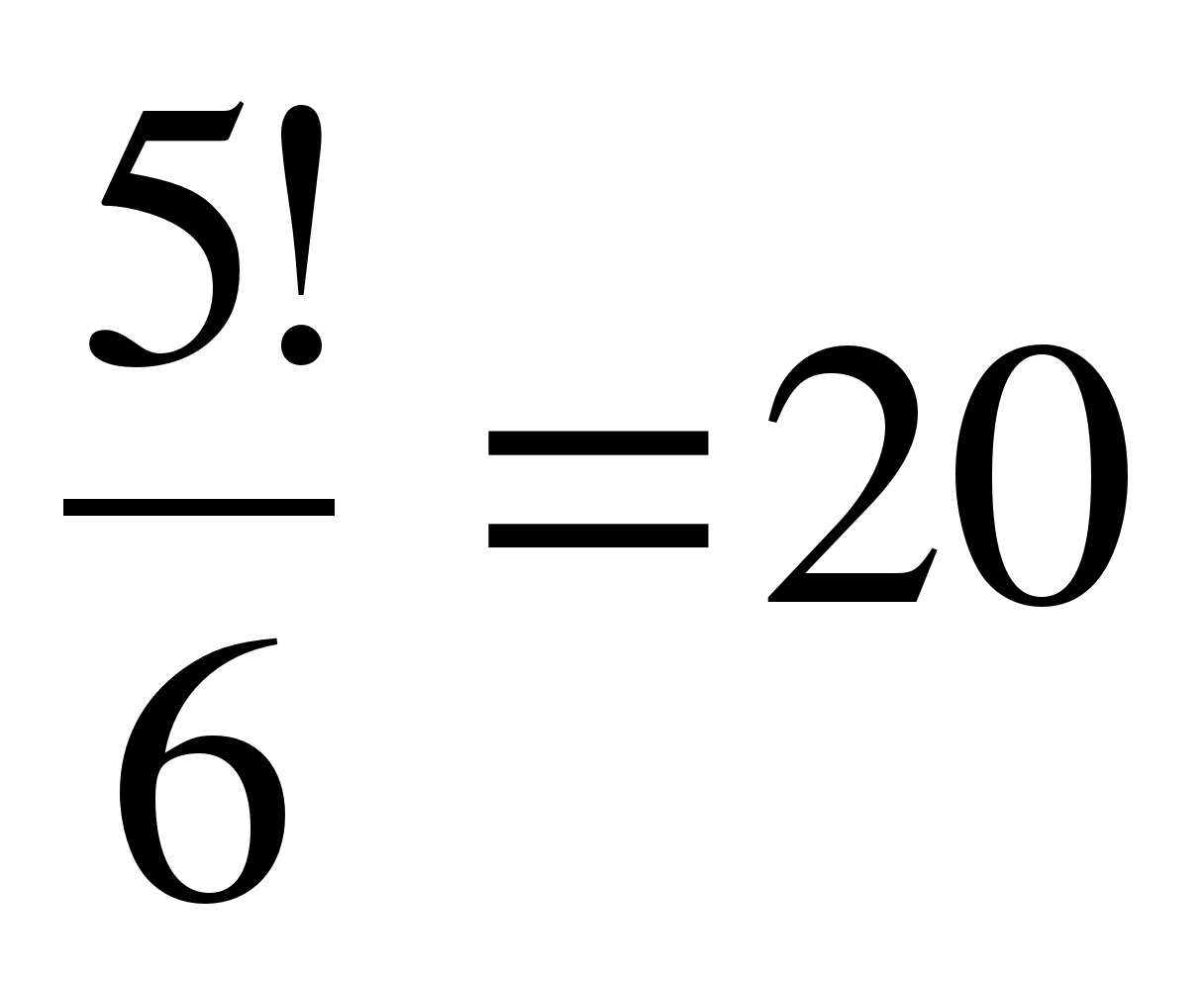

Вывод: Перестановками в такой выборке, где есть один элемент, называются перестановками с повторениями. Обозначается : Р_{(n1, n2,….., nk)}

Р(n1, n2,….., nk)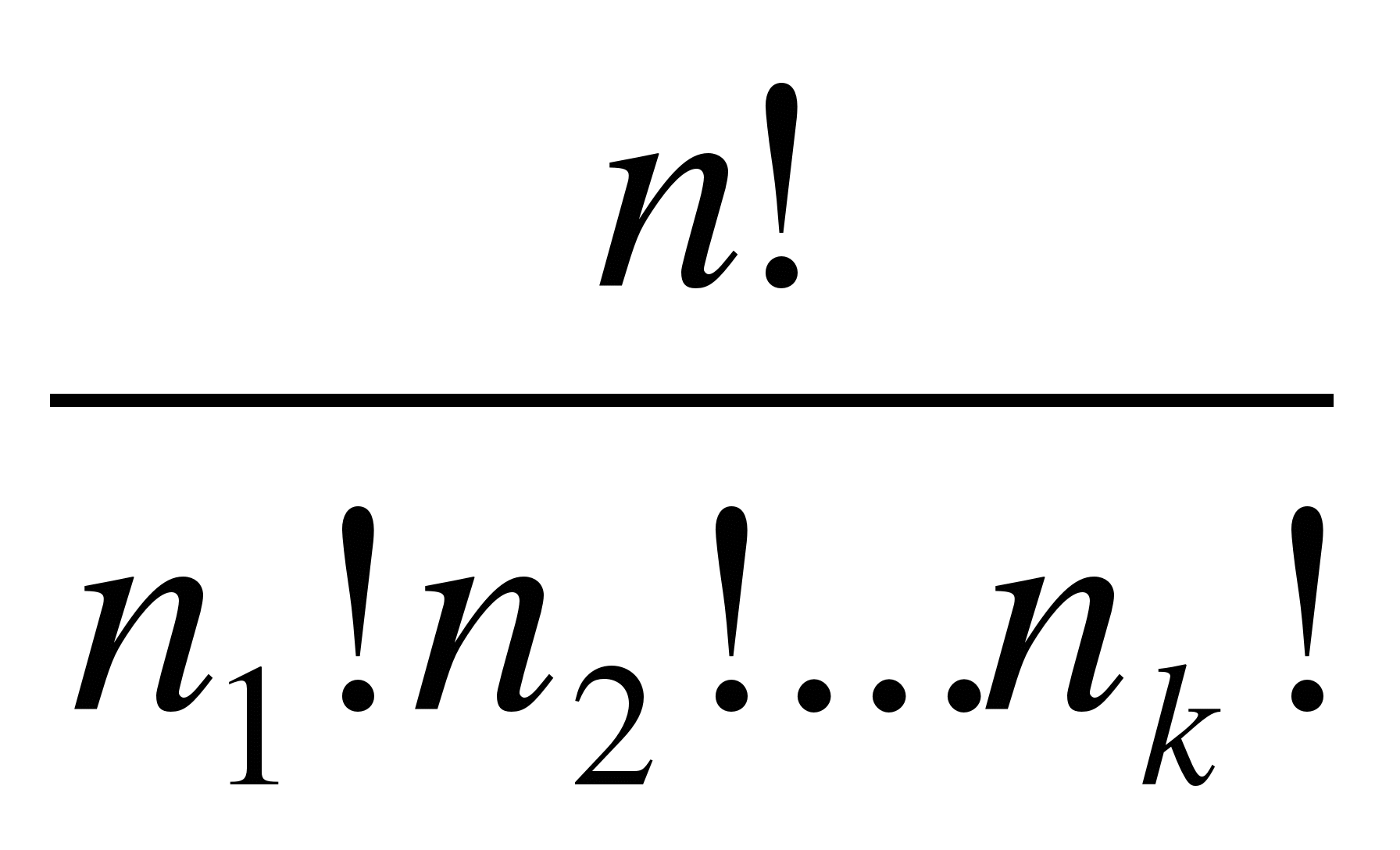₌, где n- количество повторений элементов

Задача: Сколько различных перестановок можно сделать из букв слова «МАТЕМАТИКА»

Решение:

Всего – 10 букв

«М» — 2 повтора

«А» — 3 повтора

«Т» — 2 повтора

«Е» — 1 повтор

«И» — 1 повтор

«К»- 1 повтор

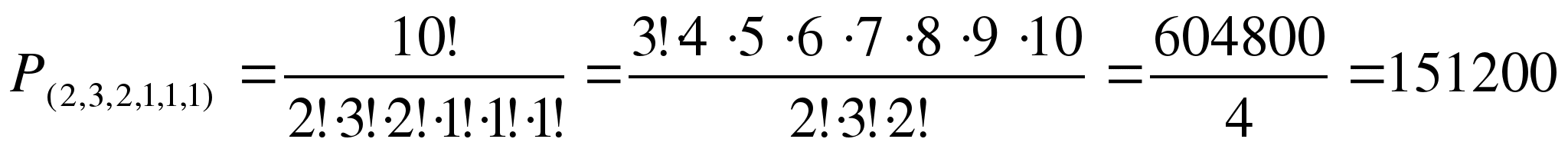перестановки

Ответ: 151200 перестановки

2. Сочетания.

Рассмотрим следующую задачу.

В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить 8 различных открыток?

Решение. Данная задача на отыскание числа сочетаний без повторений, т.к. требуется купить 8 различных открыток

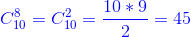
Ответ: 45 способов

Проделаем то же самое, но только определим «Сколькими способами можно купить в нем 8 открыток?

Решение.

Данная задача на отыскание числа сочетаний с повторениями из n = 10 элементов по k =8. Следовательно, она решается по формуле

 

Ответ : 24310 способов

Вывод: Иными словами, выборки которые отличаются количеством элементов хотя бы одного типа, называются сочетаниями с повторениями, а их общее число будем обозначать .

Задача: В кондитерской имеется 3 вида пирожных. Сколькими способами можно купить 9 пирожных?

Решение. В задаче требуется найти число всевозможных групп по 9 элементов, которые можно составить из данных трех различных элементов, причем указанные элементы в каждой группе могут повторяться, а сами группы отличаются друг от друга хотя бы одним элементом. Это задача на отыскание числа сочетаний с повторениями из трех элементов по девять. Следовательно,

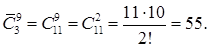
3. Размещения.

Рассмотрим задачу:

В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими различными способами могут выйти пассажиры на каждом этаже, начиная со второго?

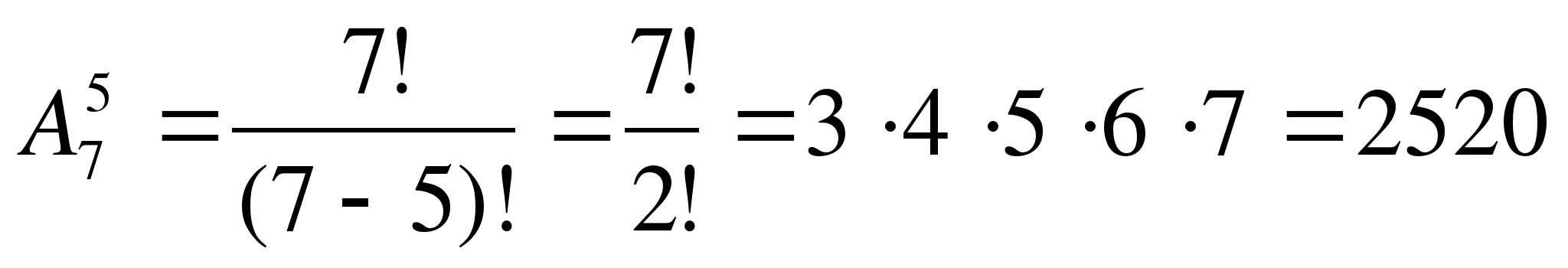способов

А теперь ту же задачу, но вопрос сформулируем иначе.

В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими способами могут выйти пассажиры на каждом этаже, начиная со второго?

Задача такого вида называется «размещения с повторением», обозначается   и вычисляется по принципу умножения.

Вычисляется по следующей формуле:

Решение. Задача сводится к распределению 5 пассажиров по 7 этажам (т. е. набор упорядоченный), причем возможны повторения (т. е. несколько пассажиров могут выйти на одном этаже). Таким образом, задача сводится к нахождению числа размещений с повторениями:

Задача: Сколькими способами девочка Яна может разложить 12 кукол по трём ящикам, если каждый ящик может вместить все куклы?

Ответ: 

IV. Закрепление.

Задача №1. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?

Решение. Число всех букв, каждая из которых записывается одним символом, равно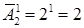 

Число всех букв, каждая из которых записывается двумя символами, равно .

Число всех букв, каждая из которых записывается тремя символами, равно .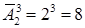

Число всех букв, каждая из которых записывается четырьмя символами, равно .

Число всех букв, каждая из которых записывается пятью символами, равно .

Число всех указанных букв будет равно 62.

Задача №2. Сколько всего чисел (не больше 100000) можно составить из цифр 1, 2, 3, 4 и 5 в каждом из которых цифры расположены в неубывающем порядке?

Решение. Это задача о числе сочетаний из пяти цифр по одному, по два, по три, по четыре и по пяти с повторениями в каждом случае. Поскольку , , 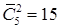, , 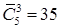, 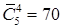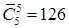то существует 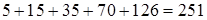чисел, удовлетворяющих условию задачи.

V. Подведение итогов занятия. Рефлексия.

(Обобщаются новые знания, делаются выводы о достигнутых целях урока. Поощряются активные студенты, выставляются обоснованные преподавателем оценки.)

1) Подведем итоги нашего занятия.

Проверь себя:

1. Соединения виды перечислить?

2. На какие они делятся ? ( повторения и без)

3. Важен ли порядок? В каких соединениях? (размещение)

4) Формулы нахождения: перестановок, размещения, соединения с повторениями и без.

2) Обсуждение и выставление оценок за урок.

3) Рефлексия:

Достиг ли ты своих целей? ______________

Оцени степень усвоения: _______________

Продолжи одно из предложений:

“Мне понятно…

“Я запомнил…

“Мне на уроке…

“Я думаю…

VI. Домашнее задание

Решите задачи:

1. Сколькими способами можно разместить 8 пассажиров по трем вагонам?

Ответ: .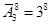

2. Сколькими способами Буратино, кот Базилио и лиса Алиса могут поделить между собой 5 одинаковых золотых монет?

Ответ: .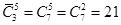

3. Сколько различных браслетов можно сделать из 5 одинаковых изумрудов, 6 одинаковых рубинов и 7 одинаковых сапфиров ( всего в браслет входит 18 камней)? ( =)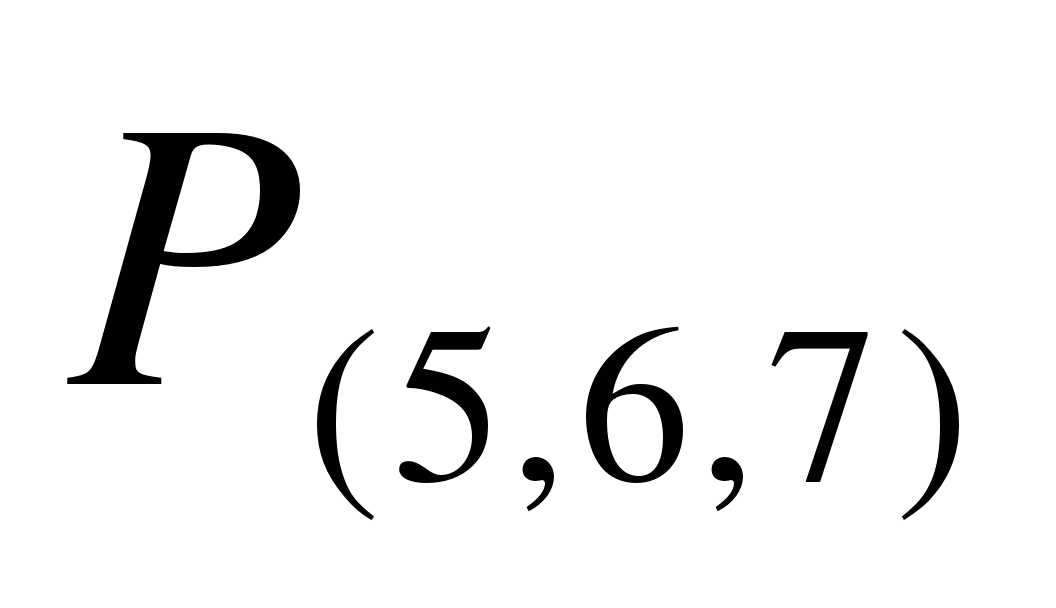

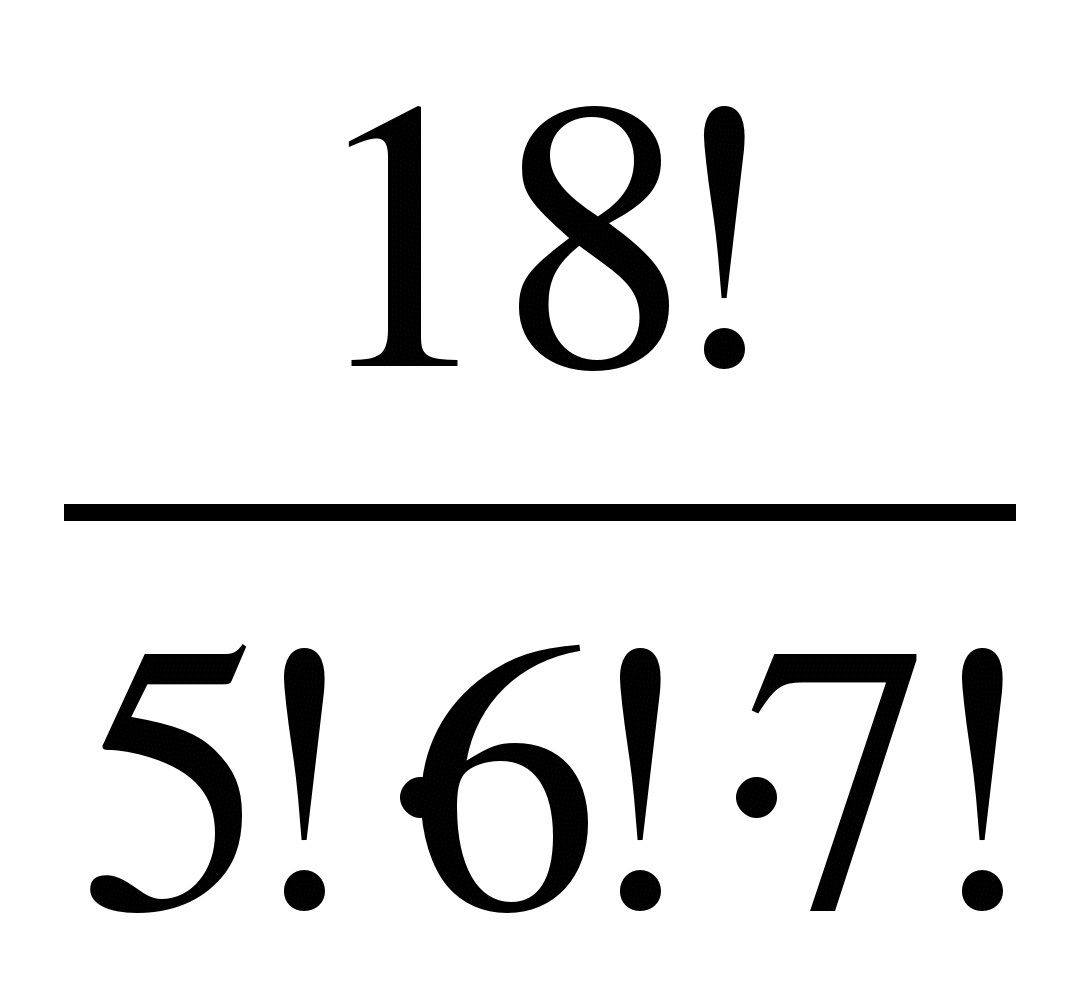Метод «Оценка плюс пример» в задачах ЕГЭ на числа и их свойства (задание 19)

«Оценка плюс пример» — это специальное математическое рассуждение, которое применяется в некоторых задачах при нахождении наибольших или наименьших значений.

Предположим, что мы ищем наименьшее значение некоторой величины A. Действуем в два этапа.

1) Оценка. Показываем, что выполнено неравенство

2) Пример. Предъявляем пример, когда достигается равенство

Сейчас покажем, как этот метод применяется в задачах. Начнем с задачи простой и умилительной. Поговорим о кроликах.

(ЕГЭ) В живом уголке четыре ученика кормят кроликов. Каждый кормит нескольких (хотя бы одного) кроликов, но не всех. Первый ученик дает порцию по 100 грамм, второй – по 200 г, третий – по 300 г., а четвертый – по 400 г.

а) Может ли оказаться, что кроликов было 15 и все они получили одинаковое количество корма?

б) Может ли оказаться, что кроликов было 15 и все они получили различное количество корма?

в) Какое наибольшее количество кроликов могло быть в живом уголке, если каждый ученик насыпал корм ровно четырем кроликам и все кролики получили разное количество корма?

а) Да, может. Например, первый и четвертый ученики кормят семь кроликов. Каждый из этих семи кроликов получает по 100 + 400 = 500 г корма. Второй и третий ученики кормят восьмерых оставшихся кроликов, которые также получат по 200 + 300 = 500 г корма.

б) Нет, не может.

Пусть среди кроликов есть «счастливец», которого покормили все школьники. Он получил максимально возможное количество корма, равное 100 + 200 + 300 + 400 = 1000 г.

Среди кроликов также может быть «невезучий», которого никто не покормил. Он получил 0 грамм корма. Значит, количество корма для одного кролика может принимать 11 различных значений: 0, 100, 200, 300… 1000 грамм.

Поскольку кроликов 15, а возможных значений только 11, среди этих пятнадцати найдутся кролики, получившие одинаковое количество корма.

в) Если каждый ученик насыпал корм четверым кроликам, то всего ученики раздали кроликам

4∙(100 + 200 + 300 + 400) = 4000 г. корма.

В пункте (б) мы выяснили, что всего может быть 11 различных значений для количества корма, которое получил кролик. Но если 11 кроликов получают различное количество корма, то общее количество корма равно 0 + 100 + 200 +…+ 1000 = 5500 грамм. Это на 1500 грамм больше, чем 4000 грамм.

Значит, накормить 11 кроликов, соблюдая все условия пункта (в), школьники не смогут.

Вариант с 10 кроликами также невозможен: даже если среди кроликов не будет того, который получил 1000 г, все равно не хватает 500 г корма.

Получается, что число кроликов не больше, чем 9. Мы оценили количество кроликов. Приведем пример, когда кроликов именно 9.

	0	100	200	300	400	600	700	800	900
1 ученик 100г		+		+	+			+
2 ученик 200 г			+	+		+			+
3 ученик 300 г					+		+	+	+
4 ученик 400 г						+	+	+	+

 

Варианты 1000 г и 500 г отсутствуют. Все условия задачи выполнены – каждый ученик покормил 4 кроликов, и все кролики получили различное количество корма.

Ответ: 9.

В пункте (в) мы применили метод «Оценка плюс пример». Это один из основных методов решения задач на числа и их свойства.

Сначала мы доказали, что число кроликов не больше 9.

После этого привели пример, когда кроликов ровно 9.

Вот более сложная задача. Здесь тоже применяется метод «Оценка плюс пример».

2. На доске написано 30 натуральных чисел (не обязательно различных), каждое из которых больше 4, но не превосходит 44. Среднее арифметическое написанных чисел равно 11. Вместо каждого из чисел на доске написали число, в два раза меньшее первоначального. Числа, которые после этого оказались меньше 3, с доски стёрли.

а) Могло ли оказаться так, что среднее арифметическое чисел, оставшихся на доске, больше 16?

б) Могло ли среднее арифметическое оставшихся на доске чисел оказаться больше 14, но меньше 15?

в) Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.

Пусть на доске были написаны числа – всего 30 чисел, причем
.

Вместо каждого из чисел написали число .

Заметим, что если , то 

Пусть на доске было k чисел, не равных 5, и 30 — k пятерок.

Поскольку среднее арифметическое 30 чисел равно их сумме, деленной на 30, сумма 30 чисел на доске равна 30 ∙ 11=330.

Пусть S – сумма k чисел, не равных 5. Тогда
, отсюда .

Пусть m – среднее арифметическое k чисел, которые остались на доске после того, как стерли числа меньшие трёх.

После того, как k чисел были уменьшены в 2 раза, их сумма стала равна , а их среднее арифметическое .

a) Может ли быть

Предположим, что  тогда

;

Пусть , то есть на доске 6 чисел, не равных 5, и 24 пятёрки.

Тогда , .

Подойдут числа:

.

б) Может ли быть  где ?

Предположим, что 

Тогда

отсюда ,

Неравенство не имеет целых решений. Значит, предположение было неверно.

в) Найдем наибольшее m, где .

Сумма k чисел, не равных 5, равна S; мы знаем, что .

;

Очевидно, m максимально при наименьшем возможном k.

Поскольку на доске k чисел, отличных от 5, каждое из этих чисел больше 5 и не превосходит 44 (по условию). Тогда их сумма
.

,

,

Поскольку k – целое,
.

Тогда
;

.

Это оценка. Приведем пример, когда k=5 и m=20,5. На доске 5 чисел, больших пяти, сумма которых равна S=205. Кроме них, на доске находится 25 пятёрок.

По условию, числа, большие пяти, могут быть равны между собой. Возьмем их равными 41 = 205 : 5.

Получим:

В этом случае m = 20,5.

В следующих статьях – читайте о других секретах решения задания 19 Профильного ЕГЭ по математике (Числа и их свойства). Приходите к нам в ЕГЭ-Студию на интенсивы по задаче 19 и на наш Онлайн-курс.

Задачи на состав числа — Мегаобучалка

Задачи, представленные в этом разделе, требуют знаний о записи десятичной формы числа. Известно, что в десятичной форме последняя цифра числа указывает число единиц, вторая цифра справа – число десятков, третья цифра справа – число сотен, четвертая цифра справа – число тысяч и т. д. Так, число 2584 содержит 4 единицы, 8 десятков, 5 сотен, 2 тысячи. Этот состав можно отразить в виде суммы 2584 = 2·1000 + 5·100 + 8·10 + 4·1. Поскольку при решении задач число единиц, десятков, сотен и т. д. приходится обозначать различными буквами, то для отличия десятичной записи числа от произведения произвольных чисел принято рисовать сверху черту. Например, запись означает, что рассматривается трехзначное число, которое можно записать в виде суммы

Задача 1. Сумма цифр двузначного числа равна 12. Если к нему прибавить 54, то получится число, записанное теми же цифрами, но в обратном порядке. Найти первоначальное число.

Решение. Обозначим искомое число

тогда

Кроме того, известно, что

Запишем эти соотношения в виде системы уравнений:

Ответ: искомое число 39.

Замечание. В задачах на состав числа обычно предполагается, что речь идет о натуральных числах, поэтому специально это обстоятельство не оговаривается. Тем не менее авторы вынуждены заметить, что иногда составители задач специально не указывают множество натуральных чисел для того, чтобы абитуриенты рассмотрели также вариант решения для целых отрицательных чисел. Так, если в представленной задаче учитывать отрицательные числа, еще одним искомым числом могло быть число –93, поскольку составляющие его цифры 9 и 3 в сумме дают 12, а сумма чисел (–93) и 54 равна (–39), т. е. числу, записанному теми же цифрами, что и первоначальное, но в обратном порядке. Поэтому, встретив подобную задачу в варианте ЕГЭ, учащийся должен выбирать ответ среди натуральных чисел, а на экзамене в вуз или предметной олимпиаде необходимо задать уточняющий вопрос экзаменатору по условию задачи.

Задача 2. Сумма цифр трехзначного числа равна 12, а сумма цифр его сотен и десятков кратна 9. Если же из искомого числа вычесть 99, то получится число, записанное теми же цифрами, но в обратном порядке. Найти это число.

Решение. Пусть искомое число тогда по условию задачи где n – натуральное число 1 или 2, в силу того что а и b однозначные числа, и

Первое и последнее соотношения приводят к уравнению

откуда , или

Кроме того, известно, что ,поэтому перейдем к системе уравнений:

Из последнего уравнения системы следует, что цифра с кратна трем, а поскольку с > 0, то число (4 – 3 n) > 0, поэтому n = 1. Теперь последнюю систему можно переписать в виде:

 

Ответ: искомое число 453.

Задача 3. Шестизначное число начинается с цифры 1. Если эту цифру записать крайней справа, сохраняя порядок остальных пяти цифр, то вновь полученное число будет втрое больше первоначального. Найти первоначальное число.

Решение. Пусть искомое число:

тогда по условию задачи,

и

Учитывая, что запишем уравнение ,

Немного преобразуем полученное равенство:

.

Число во внутренних скобках обозначим

тогда или Теперь можно записать результат

Ответ: искомое число 142857.

Задача 4. Сумму всех четных двузначных чисел разделили на одно из них, кратное 9. Получившееся частное отличается от делителя только порядком цифр. Найти делитель.

Решение. В данной задаче нам понадобится понятие арифметической прогрессии. Здесь мы используем только основные формулы. Более подробно о прогрессиях можно узнать из разд. 9, посвященного именно этой тематике.

Четные двузначные числа 10,12, 14, 16, …, 98 образуют арифметическую прогрессию, в которой первый член, а = 10, разность прогрессии d = 2, а количество членов прогрессии n = 45.

Сумма n членов арифметической прогрессии

поэтому, согласно условию задачи,

 

Полученную величину разделим на двузначное число о котором известно, что откуда где k принимает значения либо 1, либо 2, поскольку слагаемыми являются однозначные натуральные числа. Частным от деления является число Запишем исходные данные в систему:

 

 

 

 

 

Если

то откуда,

либо либо

Если же предположить, что k = 2, то получим систему

тогда и что противоречит условиям задачи. Следовательно, делителем может быть либо число 45, либо число 54.

Ответ: делителем является число 54 или число 45.

Задача 5. Если двузначное число разделить на произведение его цифр, то в частном получится 3, а в остатке 9. Если же из квадрата суммы цифр этого числа вычесть произведение его цифр, то получится данное число. Найти это число.

Решение. Напомним правило деления с остатком. Если в результате деления числа а на число b > 0 в частном получим число q, а в остатке число r, то справедливо соотношение

где

Пусть искомое двузначное число

Запишем исходные данные задачи в систему

и решим ее:

 

Из последнего уравнения получим или

Первое равенство приводит к системе:

Поскольку b > 0, то b = 3, тогда a = 6. Рассмотрим теперь случай который приводит к аналогичной системе уравнений: из которой следует, что a = 3 и b = 6.

Ответ: искомым может быть число 63 или число 36.

Разные задачи

Довольно большое количество задач не удается систематизировать и отнести к какому-либо определенному разделу. Это задачи самой разнообразной тематики, включающие как использование неравенств, так и подбор решения исходя из условий и многое другое. Подбор приведенных ниже задач не претендует на полноту, но, как надеются авторы, будет полезен учащимся при подготовке к самым разнообразным контрольным испытаниям по математике.

Задача 1. Продают три куска ткани. Из первого продали половину, из второго , а третий кусок, в котором было всей ткани, продали весь. Сколько процентов ткани продано, если всего осталось ее вдвое меньше, чем было во втором куске?

Решение. Пусть в первом куске первоначально было х метров ткани, во втором – y метров ткани, а в третьем – z метров ткани. Для удобства рассуждений составим таблицу

Таблица 3

Количество ткани в м.

Описание объекта	Первоначальное количество, м	Продано, м	Остаток, м
1-й кусок ткани	х		0,5 х
2-й кусок ткани	у
3-й кусок ткани	z	z

 

Остаток составил половину второго куска, поэтому , а количество проданной ткани в процентном отношении к первоначальному объему составляет:

Выражение, которое должно привести к конечному результату, содержит три неизвестные величины, а для его решения имеется только одно уравнение, содержащее два неизвестных. Но на самом деле ситуация не так плоха, поскольку мы можем уменьшить число неизвестных, используя данные задачи. Поскольку в третьем куске было всей ткани, то первый и второй кусок в совокупности составляют всей ткани. Следовательно,

Выразим х через y из первого уравнения тогда

Теперь подставим полученные значения для х и z в искомое выражение:

.

Ответ: было продано 75 % ткани.

Задача 2. Квартал застроен пятиэтажными и девятиэтажными домами, причем девятиэтажных домов меньше, чем пятиэтажных. Если число девятиэтажных домов увеличить вдвое, то общее количество домов станет более 24, а если увеличить вдвое количество пятиэтажных домов, то общее число домов станет менее 27. Сколько построено пятиэтажных домов и сколько девятиэтажных?

Решение. Предположим, что пятиэтажных домов было построено х штук, а девятиэтажных домов y штук.

Тогда справедлива система неравенств кроме того, из условий задачи следует, что

Задача сводится к решению системы неравенств в натуральных числах. Можно решить эту задачу графически. Подробное изложение этого метода можно найти в разд. 8. Область на плоскости ХОУ, удовлетворяющая системе неравенств, изображена на рис. 2.1. Координаты точек А(8,8), В(9,9), С(10,7) позволяют определить, что единственной точкой с целыми координатами внутри области оказывается точка (9,8). Таким образом, х = 9, у = 8.

 

Рис. 2.1. Графическое решение задачи.

 

Тот же самый результат можно получить, если решать систему неравенств аналитически, не применяя графический метод.

Как известно, неравенства одного знака можно складывать, сохраняя знак неравенства. А неравенства разных знаков можно вычитать, сохраняя знак уменьшаемого. Выполнив эти действия с неравенствами системы, получим следующие соотношения:

и .

Первое из неравенств позволяет предполагать два возможных варианта: или Если выполняется первый вариант то согласно второму условию т. е.

А так как х > 8, то единственный возможный вариант х = 9. Тогда Подстановка значений в каждое из неравенств исходной системы приводит к верному числовому неравенству. Это означает, что пара х = 9 и у = 9 является решением системы неравенств. Аналогичные рассуждения для варианта приводят к паре х = 9 и у = 7, но при этом не выполняется неравенство Следовательно, единственным решением будет х = 9 и у = 8.

Ответ: в квартале построено 9 пятиэтажных и 8 девятиэтажных домов.

Задача 3. Число учащихся в классе, повысивших свою успеваемость, заключено в пределах от 2,7 до 3,2 % от общего числа учащихся. Каково наименьшее число учащихся в классе?

Решение. Пусть х – число учащихся в классе, тогда количество учеников, которые стали учиться лучше, находится в пределах от 0,027х до 0,032х. Поскольку величина у, удовлетворяющая неравенству представляет собой натуральное число, которое надо выбрать так, чтобы значение х было минимальным из возможных, то следует предположить, что у = 1. Тогда для х получаем систему неравенств: или

Наименьшее целое значение, удовлетворяющее неравенству, равно 32.

Ответ: в классе 32 учащихся.

Задача 4. В группе из 100 туристов 70 человек знают английский язык, 45 знают французский и 23 знают оба языка. Сколько человек в группе не знают ни английского, ни французского?

Решение. В данной задаче рассматриваются операции с множествами. Удобно при решении таких задач использовать диаграммы, представляя каждое множество в виде круга.

Обозначим множество всех туристов буквой Т, множество туристов, знающих английский язык – буквой А, множество туристов, знающих французский язык – буквой Ф.

 

Рис. 2.2.Графическое решение задач.

Тогда множество туристов, знающих оба языка представляет собой пересечение множеств А∩Ф, что на рис. 2.2 представлено в виде общей части кругов А и Ф, которая содержит 23 элемента. Теперь нетрудно посчитать, что множество туристов, знающих только английский язык – это разность множеств А и А∩Ф, а их количество равно Аналогично количество туристов, знающих только французский язык, равно Таким образом, 47 туристов знают только английский язык, 22 туриста – только французский язык, 23 туриста знают оба языка, а оставшиеся человек не знают ни одного из этих языков.

Ответ: 8 человек не знают ни английского, ни французского языков.

Задача 5. Нанята бригада плотников. Если бы они явились на работу все вместе, то выполнили бы ее за 5 ч. Но они приходили друг за другом через равные промежутки времени. Первый работал в m раз больше последнего. Сколько времени работал последний плотник?

Решение. В данной задаче предполагается, что производительность всех плотников одинаковая. Поскольку объем работы неизвестен, считаем его равным единице. Пусть производительность каждого плотника составляет х единиц продукции в час, а общее число работников в бригаде равно n. Тогда справедливо равенство Промежуток времени между приходами плотников на работу обозначим за y часов, а количество времени, которое затратил на работу последний из пришедших плотников – за z. Теперь проследим за временем работы первого плотника. К моменту прихода второго работника бригады первый трудился y часов, когда появился третий – время работы первого составило 2y часов, четвертый плотник пришел на работу, когда первый проработал 3y часов, а к моменту прихода последнего время работы первого составило часов. Совместный труд всех плотников еще в течение zчасов завершил работу.

Таким образом, первый плотник работал в течение

часов и

Из последнего равенства следует, что

Суммируя части работы, выполненные каждым из плотников, получим:

Преобразуем полученное выражение:

Используем формулу суммы арифметической прогрессии

Объединим полученные равенства в систему:

из которой следует или

Ответ: последний плотник работал в течение

часов.

Замечание. Теперь, когда задача уже решена, очевидно, что некоторые неизвестные можно было не вводить.