Разное

Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

12.05.2019

Содержание

Урок 34. задачи на нахождение доли числа и числа по его доле — Математика — 3 класс

Математика, 3 класс

Урок №34. Задачи на нахождение доли числа и числа по его доле.

Перечень вопросов, рассматриваемых в теме:

— как решать задачи на нахождение доли числа и числа по его доли?

— какие наиболее эффективные способы используются для нахождения доли величины и величины по ее доле?

— каким образом сравнивать разные доли одной и той же величины?

Глоссарий по теме:

Задача – это текст, содержащий численные компоненты

Доля – это каждая из равных частей единицы.

Условие – это часть задачи, в которой рассказывается о том, что неизвестно, содержит числовые данные.

Вопрос – это часть задачи, в которой сообщается о том, что нужно узнать.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 97.

2. Волкова С. И. Проверочные работы 3 класс. Издательство «Просвещение» 2017, с. 38-39.

3. Волкова С. И. Тесты 3 класс. Издательство «Просвещение»2017, с. 20-27.

4.Рудницкая В. Н. Тесты по математике 3 класс. М.: Издательство «Экзамен», 2016 с. 44-47.

Теоретический материал для самостоятельного изучения

Появление долей связывается с практическими потребностями: задачи, где нужно производить деление на части, были очень распространены. Кроме того, в жизни человеку приходилось не только считать предметы, но и измерять величины. Люди встретились с измерениями длин, площадей земельных участков, объемов, массы тел. При этом случалось, что единица измерения не укладывалась целое число раз в измеряемой величине. Например, измеряя длину участка шагами, человек встречался с таким явлением: в длине укладывалось десять шагов, и оставался остаток меньше одного шага.

Таким образом, во всех цивилизациях понятие доли возникло из процесса дробления целого на равные части.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Русский термин «дробь», как и его аналоги в других языках, происходит от лат. fractura, который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять.

Доля это каждая из равных частей единицы. Название доли зависит от того, на сколько равных частей разделили единицу. Разделили на две части название доли «половина», на три — «треть», на четыре — «четверть».

Использование знаний о долях применяется для решения задач.

Рассмотрим рисунок.

12 см

1) Полоску длиной 12 см разделили на 2 части. Одна часть, или ее называют одна вторая, составляет 6 см. Составим выражение:

12 : 2 = 6 см

2) Полоску этой же длины разделим на 3 части. Одна третья составляет 4 см.

12 см

12 : 3 = 4 см

3) Найдем одну шестую полоски. Одна шестая составляет 2 см.

12 см

12 : 6 = 2 см

Вывод: чтобы найти долю от числа, надо число разделить на количество частей (долей).Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Рассмотрим рисунок.

1) Длина второй части отрезка составляет 8 см. Чему равна длина всего отрезка?

? см

8 ∙ 2 = 16 см

По 8 см возьмем 2 раза получим 16 см.

2) Длина четвертой части отрезка составляет 4 см. Найдем длину всего отрезка.

? см

4 ∙ 4 = 16 см

4 умножим на 4, получим 16 см.

3) Найдем длину отрезка, если восьмая часть составляет 2 см.

? см

2 ∙ 8 = 16 см

Вывод: чтобы найти число по его доле, надо долю этого числа умножить на число долей.

Решим задачу.

6 листов составляют половину тетради. Сколько всего листов в тетради? Половин в тетради может быть только две. Если в каждой по 6 листов, то вся тетрадь содержит: 6 ∙ 2 = 12 (листов).

Вывод: чтобы найти число по его доле, надо долю этого числа умножить на число долей.

Решим задачу.

Чему равна треть суток?

В сутках 24 часа. Чтобы найти треть суток, нужно 24:4=8 (часов).

Вывод: чтобы найти долю от числа, надо число разделить на количество частей (долей)

Задания тренировочного модуля:

1.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Выберите верный ответ.

В мотке 24 м кружев. Отрезали восьмую часть мотка. Сколько кружев отрезали?

16 м

32 м

3 м

4м

Правильный ответ:

3м

2. Соотнесите ответы.

Длина коридора 12 м. Мальчик прошел по коридору 4 м. Какую часть коридора он прошёл?

Правильный ответ:

Задачи с числами. ЕГЭ по математике

а) Да. Приведём пример: 24,32,40,48,56,64,72.

б) Предположим, что такая прогрессия существует. Очевидно, она возрастающая. Обозначим a_{l} — наименьший, кратный 24, член прогрессии. Тогда a_{l}, a_{l+i},…,a_{l+8i} — 9 первых членов прогрессии, кратных 24, причем l+8i \leq 30, откуда i \leq 3, так как l \geq 1, а l+9i > 30, тогда 30-9i < l \leq 30-8i.

Если i=3,\, 3 < l \leq6;

Если i=2,\, 12 < l \leq14;

Если i=1,\, 21 < l \leq22.

В каждом из этих случаев получаем противоречие с предположением, что a_{l} — наименьший, кратный 24, член прогрессии (достаточно рассмотреть хотя бы a_{l-i}).Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Итак, предположение неверно, значит, не существует такой прогрессии, в которой среди чисел a_{1}, a_{2},…,a_{30} ровно 9 чисел делятся на 24.

в) Среди любых 24 подряд идущих членов ровно один делится на 24. Пусть 3n=24s+r, где s,r \in \mathbb Z, r \geq 0, s \geq 0, 0 \leq r \leq 23 (r — остаток от деления n на 24). Тогда среди чисел a_{1},a_{2},…,a_{3n} на 24 делятся s или (s+1) чисел. Среди чисел a_{3n+1}, a_{3n+2},…,a_{6n} на 24 тоже делятся не менее s чисел. Если n \geq 24, то среди чисел a_{6n+1}, a_{6n+2},…,a_{7n} хотя бы одно делится на 24. Тогда среди чисел a_{3n+1},…,a_{7n} на 24 делятся хотя бы (s+1), значит, не меньше, чем среди чисел a_{1}, a_{2},…,a_{3n}.

Далее, среди чисел a_{1},…, a_{3n} на 24 делится чисел не более, чем частное \frac{3n}{24}=\frac{n}{8}, округлённое с избытком, и среди чисел a_{3n+1},…,a_{7n} не менее, чем частное \frac{4n}{24}=\frac{n}{6}, округленное с недостатком. Если 18 \leq n < 24, то \frac{n}{6} \geq 3, и частное, округлённое с недостатком, равно 3.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи При этом \frac{n}{8} < \frac{24}{8}=3, и частное \frac{n}{8}, округлённое с избытком, равно 3. Значит, среди членов a_{1},…,a_{3n} чисел, делящихся на 24, не может быть строго больше, чем среди чисел a_{3n+1},…,a_{7n} \geq 18.

Таким образом, n \leq 17. Приведём пример подходящей последовательности для n=17. Пусть a_{1}=22. Тогда среди чисел a_{1},…,a_{51} на 24 делятся a_{3}, a_{27} и a_{51}, а среди чисел a_{52},…,a_{119} — числа a_{75} и a_{99}.

Гимнастика для ума: 10 увлекательных задач с числами

Для удобства советуем вам запастись бумагой и ручкой.

— 1 —

Есть семь цифр: 1, 2, 3, 4, 5, 6, 7. Соедините их арифметическими знаками так, чтобы получившееся выражение было равно 55. Возможно несколько вариантов решения.

Показать ответ

Скрыть ответ

Вот три варианта решения этой задачи:

 

1) 123 + 4 − 5 − 67 = 55;
2) 1 − 2 − 3 − 4 + 56 + 7 = 55;
3) 12 − 3 + 45 − 6 + 7 = 55.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

— 2—

В выражении 5 × 8 + 12 ÷ 4 − 3 расставьте скобки так, чтобы его значение было равно 10.

Показать ответ

Скрыть ответ

(5 × 8 + 12) ÷ 4 − 3. Проверим, действительно ли значение выражения равно 10. Выполним действия в скобках, затем деление и вычитание: (40 + 12) ÷ 4 − 3 = 52 ÷ 4 − 3 = 13 − 3 = 10.

— 3 —

Составьте выражение из семи четвёрок, арифметических знаков и запятой таким образом, чтобы его значение было равно 10.

Показать ответ

Скрыть ответ

44,4 ÷ 4 − 4,4 ÷ 4. Проверим полученное выражение, выполнив сначала деление, а потом вычитание: 11,1 − 1,1 = 10.

— 4 —

Если перемножить эти три целых числа, то результат будет таким же, как если бы мы их складывали. Назовите эти числа.

Показать ответ

Скрыть ответ

Числа 1, 2, 3 при перемножении и сложении дают один и тот же результат: 1 + 2 + 3 = 6; 1 × 2 × 3 = 6.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

— 5 —

Цифру 9, с которой начиналось трёхзначное число, перенесли в конец числа. В результате получилось число на 216 меньшее. Найдите исходное число.

Показать ответ

Скрыть ответ

Пусть 9АБ — это исходное число, тогда АБ9 — новое число. Следуя условиям задачи, составим следующее равенство: 216 + АБ9 = 9АБ.

 

Найдём число единиц: 6 + 9 = 15, поэтому Б = 5. Подставим в выражение полученное значение: 216 + А59 = 9А5. Найдём число сотен: 9 − 2 = 7, значит А = 7. Проверим: 216 + 759 = 975. Это и есть исходное число.

— 6 —

Если от задуманного трёхзначного числа отнять 7, то оно разделится на 7; если отнять 8, оно разделится на 8; если отнять 9 — разделится на 9. Найдите это число.

Показать ответ

Скрыть ответ

Чтобы определить задуманное число, нужно вычислить наименьшее общее кратное 7, 8 и 9. Для этого перемножим эти числа между собой: 7 × 8 × 9 = 504.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Проверим, подходит ли нам это число:

 

504 − 7 = 497; 497 ÷ 7 = 71;
504 − 8 = 496; 496 ÷ 8 = 62;
504 − 9 = 495; 495 ÷ 9 = 55.

 

Значит, число 504 удовлетворяет условию задачи.

— 7 —

Посмотрите на равенство 101 − 102 = 1 и переставьте одну цифру так, чтобы оно стало верным.

Показать ответ

Скрыть ответ

101 − 102 = 1. Проверим: 101 − 100 = 1.

— 8 —

Записано 99 чисел: 1, 2, 3, … 98, 99. Подсчитайте, сколько раз в этой цепочке встречается цифра 5.

Показать ответ

Скрыть ответ

20 раз. Вот числа, которые удовлетворяют условию: 5, 15, 25, 35, 45, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 65, 75, 85, 95.

— 9 —

Ответьте, сколько существует двузначных чисел, у которых цифра десятков меньше цифры единиц.

Показать ответ

Скрыть ответ

Чтобы найти решение, будем рассуждать следующим образом: если в разряде десятков стоит цифра 1, то в разряде единиц — любая из цифр от 2 до 9, а это восемь вариантов выбора.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Если в разряде десятков стоит цифра 2, то в разряде единиц — любая из цифр от 3 до 9, а это семь вариантов выбора. Если в разряде десятков стоит цифра 3, то в разряде единиц — любая из цифр от 4 до 9, а это шесть вариантов выбора. И так далее.

 

Подсчитаем общее количество комбинаций: 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36.

— 10 —

В числе 3 728 954 106 уберите три цифры так, чтобы оставшиеся цифры в том же порядке представляли собой наименьшее семизначное число.

Показать ответ

Скрыть ответ

Чтобы искомое число было наименьшим, нужно, чтобы оно начиналось на наименьшую цифру из возможных, поэтому убираем цифры 3 и 7. Теперь надо, чтобы после двойки шла наименьшая цифра. Если зачеркнуть восьмёрку, на её месте окажется девятка и число увеличится. Поэтому убираем 9. Вот какое число получится: 2 854 106.

Читайте также 🤔

Задачи на состав числа

Задачи на состав числа решают, как правило, с помощью системы уравнений.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Если речь идет о двузначном числе, за x принимают количество десятков, за y — количество единиц числа. Тогда двузначное число равно 10x+y.  Рассмотрим примеры решения задач на состав числа.

1) Найти двузначное число, которое в 4 раза больше суммы своих цифр и в полтора раза больше их произведения.

Решение:

Пусть x — количество десятков в записи данного двузначного числа, а y — количество единиц. Тогда число равно 10x+y, сумма его цифр — (x+y), а произведение цифр — xy. По условию задачи известно, что число в 4 раза больше суммы своих цифр и в 1,5 раза больше их произведения. Составим систему уравнений и решим ее:

   

Упростим первое уравнение:

   

   

   

   

Полученное выражение подставляем во второе уравнение:

   

   

Первый корень не удовлетворяет условию задачи (в двузначном числе число десятков не может быть равным нулю). Таким образом,

   

Следовательно, данное двузначное число равно 48.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Ответ: 48.

 2) Сумма квадратов цифр двузначного натурального числа равна 53. Если из этого числа вычесть 45, получим число, записанное теми же цифрами, но в обратном порядке. Найти данное число.

Решение:

Пусть x — число десятков данного двузначного числа, а y — число его единиц. Тогда число равно 10x+y. Сумма квадратов его цифр x²+y², что по условию задачи равно 53. Значит, x²+y²=53.

Если из данного числа вычесть 45, получим 10x-y-45. В условии сказано, что получится число, записанное теми же цифрами, но в обратном порядке: 10y+x. Отсюда: 10x-y-45=10y+x. Составим и решим систему уравнений:

   

Упростим второе уравнение:

   

   

Подставляем полученное выражение в первое уравнение:

   

   

   

Второй корень не подходит по смыслу задачи. Находим y=7-5=2. Значит, данное двузначное число равно 72.

Ответ: 72.

Если в задаче на состав числа речь идет о трехзначном числе, вводим три переменные: x — количество сотен, y — количество десятков, z — количество единиц.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи {6}=3 \times 1\ 000\ 000=3\ 000\ 000$ натуральное число.

Задача 2

Какое из следующих утверждений верно?

Задача 3

Верно ли, что $3\in Z$?

Решение:
Да, это верно. Множество целых чисел $\mathbf{Z=}\left\{ ……-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7…….\right\} $.

Оно включает в себя все натуральные числа, все отрицательные числа и число ноль.

Задача 4

Верно ли, что $-3\in N$?

Задача 5

Верно ли, что $\sqrt{2}\in Q$

Задача 6

$\frac{3}{4}$ рациональное число и $2$ натуральное число. Каким числом является $\frac{3}{4}+2$?

Задача 7

Верно ли следующее утверждение?
Каждое натуральное число также является целым числом.

Задача 8

Верно ли следующее утверждение?
Каждое натуральное число также является рациональным числом.

Задача 9

Верно ли следующее утверждение?
Каждое иррациональное число можно записать в виде дроби.

Задача 10

Верно ли, что $-2\in Q$?


Задача 11

Верно ли, что
$\pi \in I$?

Задача 12

Сколько из следующих чисел являются целыми числами?
$0,$ $\frac{-4}{2},2^{3},\frac{5}{2},e,\sqrt{2},-\sqrt{9}$

Задача 13

Пусть число $n=\frac{3}{5}-2$
Какое из следующих утверждений является ложным?

Задача 14

Если $m,n$ рациональные числа, то какое из следующих утверждений верно?

Задача 15

Число $3,25$ является рациональным или иррациональным?

Задача 16

Число $n=2,151515151515.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи ……$ имеет бесконечные количество десятичных знаков и 15 повторяется бесконечное количество раз.
Является ли оно рациональным или иррациональным?

Решение:
Хотя $n=2,151515151515…….$ имеет бесконечные количество десятичных знаков, это рациональное число.

Докажем это.

Прежде всего, давайте умножим обе стороны на $100$
$100n=215,1515151515…….$
Мы видим, что точка перемещается на два места вправо, но даже результат все еще имеет бесконечные количество десятичных знаков.

Давайте вычтем оба уравнения $\left\{ \begin{array}{c} 100n=215,1515151515……. \\ n=2,151515151515…….% \end{array}% \right\} $

Мы получаем $100n-n=215-2\Longrightarrow 99n=215-2\Longrightarrow 99n=213$

$n=\frac{213}{99}$ таким образом число $n=2,151515151515…$ является рациональным.

Задача 17

Является ли число $\frac{\sqrt{5}}{2}$ рациональным или иррациональным?

Решение:
Хотя это число записывается в виде дроби, оно не рациональное, потому что $\sqrt{5}$ иррациональное.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи {6n + 3} + 1 ⋮ 148$? Отправить решение


Задача 3. Докажите, что для любых&nbsp$a$, $b$ и&nbsp$c$ , таких, что&nbsp$a\cdot b\cdot c\ne0$, выполняется 1)   $НОД(a,b,c) = НОД(a,НОД(b,c)) = НОД(НОД(a,b),c)$; 2)   $НОК(a,b,c) = \frac{|abc|\cdotНОД(a,b,c)}{НОД(a,b)\cdotНОД(b,c)\cdotНОД(a,c)}$. Отправить решение


Задача 4. Существует&nbspли число, которое при делении на&nbspчисла&nbsp$2$, $3$, $4$, $5$ и&nbsp$6$ даёт в&nbspостатке соответственно   1) $1$, $2$, $3$, $4$, $5$;    2) $0$, $1$, $2$, $3$, $4$;    3) $0$, $1$, $2$, $3$, $2$? Отправить решение


Задача 7.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи 2}) = \frac{n + 2}{2n + 2}$. Отправить решение


Задача 9. Решите в&nbspцелых числах уравнения 1) $7x + 5y = 1$;   2) $27x — 24y = 1$;   3) $12x — 33y = 9$; 4) $-56x + 91y = 21$;   5) $344x — 215y = 86$;   6) $3x + 5y +7z = 1$. Отправить решение


Задача 11. Найдите такие числа&nbsp$a$ и&nbsp$b$, что&nbsp$ax + by = 1$ при 1) $x=7 , y=9$;   2) $x=17 , y=19$;   3) $x=27 , y=29$;   4) $x=37 , y=39$; 5) $x=47 , y=49$.   Отправить решение


Задача 12.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи n$? Отправить решение


Математика. Решаю примеры и задачи. Число и цифра 9

Тема:Решаю примеры и задачи.Число и цифра 9

Школа —Лицей

Дата:

Ф.И.О педагога:

Предшкольный класс:

Количество присутствующих:

Количество отсутствующих:

Цель обучения

Решать простейшие примеры и задачи на основе наглядности. Знать число и цифру 9.

Предполагаемый результат

Все ученики будут: решать простейшие примеры и задачи на основе наглядности.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Знать число и цифру 9.

Многие воспитанники будут: самостоятельно составлять и решать простейшие примеры и задачи на основе наглядности. Знать состав числа 9.

Некоторые воспитанники будут : устанавливать связь сложения и вычитания.

Языковая цель

Воспитанники могут: объяснить, как решить простейшие примеры и задачи на основе наглядности и решать путем пересчета групп предметов.

Задача, пример,сложение,вычитание.

Вопросы для обсуждения:

Расскажите, какой знак вы выберете для записи решения задачи, почему?

Можете ли вы объяснить, какие знаки помогли вам записать примеры?

Письмо:

Впишите числа, обведите числа.

Предшествующие знания

Сложение и вычитание, знаки +,-,=.

План

Планируемое время

Запланированная деятельность

Ресурсы

Актуализация знаний

-Ребята, давайте вспомним свами какое число и цифру мы изучали свами на прошлом уроке.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи А вспомнить нам поможет игра «в столовой»

Дети раскладывают тарелочки и стаканы на столах. Можно провести работу на сравнение групп предметов.

-Чего больше- тарелок или стаканов?

-Насколько больше?

-Как сделать, чтобы их стало поровну?

Все действия сопровождаются выкладыванием примеров на карточках.

-Так какую цифру мы изучали на прошлом уроке? (8)

— Молодцы!

— Давайте найдем ее на цифровом луче. (Посчитали)

-Состав числа 8. (дети показывают на карточках состав числа).

-А если мы прибавим к 8 еще один, то какое число получится?

-Правильно 9!

-Сегодня мы будем изучать число и цифру 9, составлять задачи и решать примеры.

Карточки с числами от 1до 9, Знаки +,-,=.

Постановка цели (проблемная ситуация)

А теперь ребята, давайте обведем нашу цифру 9.

Цифра девять. Это есть —
Перевёрнутая шесть.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи
Наверху рисуй кружок,
Вниз — дугу наискосок.

Начинай писать с кружка,
Да не делай уголка.
У девятки нет углов:
Круг, дуга — и знак готов!

Шаг 1. Этот знак рисуем следующим образом:

сначала

рисуем верхнюю часть, поставив точку немного ниже

верхнего угла клеточки по ее правой стороне. Ведем

линию вниз, влево, а потом вверх. Должен получиться

небольшой овал с наклоном вправо.

Шаг 2. Дойдя до точки, с которой начали рисование,

проходим ее, опускаясь к нижней границе клеточки.

Закругляем линию, поднимая «хвостик» девятки чуть выше

нижнего ребра клетки

-Сейчас мы с вами разберем, из каких же чисел состоит число 9.

Состав числа 9 и работа с числовым лучом.

Домики с составом числа 9.

Применение изученного и коррекция знаний и умений.

Продолжим нашу игру.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Сколько ребят пришло в столовую? Мальчиков -4

Девочек -5

4+5=9

Сколько накрыто тарелок с блинами?

Сколько тарелок с яичницой?

Сколько тарелок всего?

3+6=9

Сколько стаканов с соком?

Сколько стаканов с молоком?

Сколько всего?

2+7=9

(Дети составляют пример в группах, чья группа составила быстрее ,те выходят к доске)

А так как вы успели заметить ,по предыдущему заданию . Что интересного вы успели заметить?

-Правильно! Везде в ответе у нас получилось 9.

На этом занятии впервые встречается не только

составление примеров с ответом 9, но и вычитание из 9.

Работа в группах. Решить примеры в задании

№3.

Азбука-тетрадь,

раздаточный

счетный

материал,

карточки с

числами и

знаками.

Рефлексия.

—Ребята у вас на столах лежат конверты .Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Откройте их, пожалуйста и посмотрите ,что в них находится.

-Правильно, это груши.

-Как вы думаете ,почему именно груши?

-Посчитайте их.

-Сколько груш? (9)

-А почему именно 9 груш?

-Правильно! Потому что мы сегодня изучали число и цифру 9.

Педагог подводит итог, поощряет детей.

Предлагает оценить свою работу на занятии при помощи смайликов.

Веселый смайлик- если все понятно и урок понравился.

Грустный смайлик-мало что было понятно и урок не понравился.

«Числовое» слово Задачи

«Число» Проблемы со словами

«Числовые» проблемы со словами довольно надуманы, но они также довольно стандартные, поэтому вам следует научитесь обращаться с ними. Ведь смысл этих проблем не их отношение к «реальной жизни», а ваша способность чтобы извлечь математику из английского.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

  • Сумма два последовательных целых числа — 15. Найдите числа.

    Они дали мне две части информации здесь. Во-первых, я знаю, что добавляю два числа, а их сумма равна пятнадцати. Во-вторых, я знаю, что числа — красивые аккуратные круглые числа (например, –3 или 6), не беспорядочные (например, –4.628 или 17 / 32 ), и что второе число на единицу больше первого.Этот последняя информация исходит из того факта, что «последовательный целые числа «(или» последовательные целые числа «, если они ограничивают возможности только положительными числами) находятся на расстоянии одной единицы. Примеры «последовательных целых чисел» будет –12 и –11, 1 и 2, и 99 и 100. Используя эти факты, я могу настроить перевод.

    Представляю первый номер — « n ».Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Тогда второе число должно быть « n + 1». Тогда их сумма составляет:

      n + ( n + 1) = 15
      2 n + 1 = 15
      2 n = 14
      n = 7 Авторские права © Элизабет Стапель 2000-2011 Все права защищены

    Упражнение не спрашивал у меня значение переменной n ; он попросил идентичность двух чисел.Так что мой ответ не « n = 7»; фактический ответ:

  • Продукт двух последовательных отрицательных четных чисел равно 24. Найдите числа.

    Они сказали мне немного об этих двух числах: числа даже и они отрицательные. (Тот факт, что они отрицательные может помочь, если я найду два решения — положительное и отрицательный — так что я буду знать, какой выбрать.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи ) Поскольку четные числа находятся два друг от друга (например, –4 и –2 или 10 и 12), то я также знаю, что второе число на два больше, чем первый. Я также знаю, что когда я умножаю два числа, Получу 24. Другими словами, если первое число будет « n » и второе число будет « n + 2», У меня:

    Тогда решения равны n = –6 и n = 4.С числа, которые я ищу, отрицательны, я могу игнорировать «4» и возьмем n = –6. потом следующее число — n + 2 = –4, и ответ

В приведенном выше упражнении один из ответов был одним из решений уравнения; то Другой ответ был отрицательным по сравнению с другим решением уравнения.Предупреждение: не думайте, что вы можете использовать оба решения, если просто измените знаки на то, что вам нравится.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Хотя это часто «работает», не всегда работает, и точно раздражать учителя. Выбросьте неверные результаты и решите правильно для действительных.

  • В два раза больше из двух чисел больше трех, чем в пять раз меньше, и сумма в четыре раза большего и в три раза меньшего 71 год.Какие числа?

Пункт упражнений как это, чтобы вы попрактиковались в разворачивании и раскручивании этих слова и превращение слов в алгебраические уравнения. Смысл находится в решении, а не в относительной «реальности» проблема. Тем не менее, как вы это решите? Лучший первый шаг — это для начала маркировки:

      больший номер: x
      меньшее число: y

      вдвое больше больше: 2 x
      в три раза меньше, чем в пять раз: 5 y + 3
      соотношение между («есть»): 2 x = 5 y + 3

      четыре раза больший: 4 x
      в три раза меньше: 3 y
      соотношение между («сумма»): 4 x + 3 y = 71

    Теперь у меня два уравнения с двумя переменными:

    Решу, скажем, первое уравнение для x :

    Тогда воткну правую часть этого во второе уравнение вместо из « x «:

    Теперь, когда у меня есть значение для y , Я могу решить для x :

    Как всегда, я не забудьте ответить на вопрос, который был задан на самом деле.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Решение здесь не « x = 14», но это следующее предложение:

      Более крупный число 14, и меньшее число 5.

Уловка для выполнения этот тип проблемы состоит в том, чтобы обозначить все очень явно. До того как вы привыкли делать это, не пытайтесь отслеживать вещи в твоей голове.Сделайте то же, что и в последнем примере: четко обозначьте каждый шаг. Когда вы это делаете, эти проблемы обычно работают выходит довольно легко.

Верх | Вернуться к индексу

Цитируйте эту статью как:

Стапель, Елизавета. «Задачи со словом« число »». Purplemath .Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Доступна с
https://www.purplemath.com/modules/numbprob.htm . Доступ [Дата] [Месяц] 2016 г.

Числовое слово Проблемы с решениями

Задача 1:

Сумма пятикратного числа, 8 равно 48. Найдите число.

Решение:

Пусть число будет «x»

Тогда

5x + 8 = 48

Вычтем 8 с обеих сторон.

(5x + 8) — 8 = 48 — 8

5x = 40

Разделим обе стороны на 5.

5x / 5 = 40/5

x = 8

Итак, число равно 8.

Задача 2:

Число состоит из трех цифр, средняя из которых равна нулю, а сумма других цифр равна 9. Число, образованное перестановкой первой и третьей цифр, больше исходного числа на 297. Найдите номер.

Решение:

Пусть «x0y» будет требуемым трехзначным числом.(Согласно данной информации, средняя цифра равна нулю)

«Сумма других цифр равна 9» —-> x + y = 9 —— (1)

«Замена первой и третьей цифры «———> y0x

Из информации, представленной в вопросе, мы можем получить

y0x — x0y = 297

(100y + x) — (100x + y) = 297

100y + x — 100x -y = 297

-99x + 99y = 297

-x + y = 3 ——— (2)

Решая (1) и (2), получаем x = 3 и y = 6

Итак,

x0y = 306

Итак, необходимое число — 306.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Задача 3:

Из двух чисел 1/5 большего числа равно 1/3 меньшего, а их сумма равна 16. Найдите числа.

Решение:

Пусть «x» и «y» будут двумя необходимыми числами, так что

x> y.

Из точки «1/5 большего равно 1/3 меньшего» имеем

(1/5) x = (1/3) y

3x = 5y

3x — 5 y = 0 ——— (1)

Из точки «их сумма равна 16» имеем

x + y = 16 ———- (1)

Решая (1) и (2), получаем x = 10 и y = 6.

Итак, два числа — 10 и 6.

Задача 4:

Число от 10 до 100 в пять раз превышает сумму его цифр. Если к нему добавить 9, цифры меняются местами. Найдите номер.

Решение:

Пусть «xy» будет требуемым числом от 10 до 100. (Двухзначное число)

«Число от 10 до 100 в пять раз больше суммы его цифр»

Из информации выше, мы имеем

xy = 5 (x + y)

10x + y = 5x + 5y

5x — 4y = 0 ——- (1)

«Если к нему добавить 9, цифры перевернуты «

Из приведенной выше информации имеем

xy + 9 = yx

10x + y + 9 = 10y + x

9x — 9y = -9

x — y = -1 — ——- (2)

Решая (1) и (2), получаем x = 4 и y = 5.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Итак, необходимое число — 45.

Задача 5:

Одно число в три раза больше другого числа на 2. Если в 4 раза меньшее число превышает большее на 5, найдите числа.

Решение:

Пусть «x» и «y» будут такими двумя числами, что x> y

Дано: одно число в три раза больше другого числа на 2

Итак, мы имеем x = 3y + 2 ——— (1)

Дано: в 4 раза меньшее число превышает большее на 5

Итак, мы имеем 4y = x + 5 ——— (2)

Вставив (1) в (2), мы получим

4y = 3y + 2 + 5

4y = 3y + 7

4y = 3y + 7

y = 7

Подключив y = 7 дюймов (1 ), получаем x = 3 (7) + 2

Следовательно, x = 23

Итак, два числа — 23 и 7.

Задача 6:

Двузначное число в семь раз больше суммы его цифр. Число, образованное перестановкой цифр, на 18 меньше заданного числа. Найдите данное число.

Решение:

Пусть xy будет требуемым двузначным числом.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Дано: Двухзначное число в 7 раз превышает сумму его цифр.

Итак, имеем

xy = 7 (x + y)

10x + y = 7x + 7y

10x + y = 7x + 7y

3x — 6y = 0

x — 2y = 0 — —— (1)

Дано: Число, образованное перестановкой цифр, на 18 меньше заданного числа

Итак, у нас есть

xy — yx = 18

(10x + y) — (10y + x) = 18

10x + y — 10y — x = 18

9x — 9y = 18

x — y = 2 ——— (2)

Решение (1) и (2 ), получаем x = 4 и y = 2

xy = 42

Итак, необходимое число равно 42.

Задача 7:

Если при делении числа на 296 получается остаток 75, найдите остаток от 37 деления того же числа.

Решение:

Пусть число будет ‘x’

Тогда x = 296k + 75, где ‘k’ является частным, когда ‘x’ делится на ‘296’

В предложении выше мы имеем 296 умноженное на константу «k», к этому добавляется 75. В этой форме мы рассматриваем число 75 как остаток от деления числа x на 296.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Мы хотим найти остаток от деления числа «x» на 37. Для этого нам нужно иметь 37 в том месте, где у нас 296 в приведенном выше уравнении.

Таким образом, мы можем записать 296 как 37 умножить на 8 и 75 как 37 умножить на 2 плюс 1. Это показано ниже.

x = 37 × 8k + 37 × 2 + 1

x = 37 (8k + 2) + 1

Итак, остаток равен «1», когда число «x» делится на 37.

Задача 8:

Найдите наименьшее число, которое при делении на 35 дает остаток 25, при делении на 45 остается остаток 35, а при делении на 55 дает остаток 45.

Решение:

Для каждого делителя и соответствующего остатка мы должны найти разницу.

35-25 = 10

45-35 = 10

55-45 = 10

мы получаем разность 10 (для всех делителей и соответствующих остатков)

Теперь нам нужно найти НОК для ( 35,45,55) и вычтите разницу из НОК

L.C.M of (35, 45, 55) = 3465

Итак, необходимое наименьшее число равно

= 3465 — 10

= 3455

Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.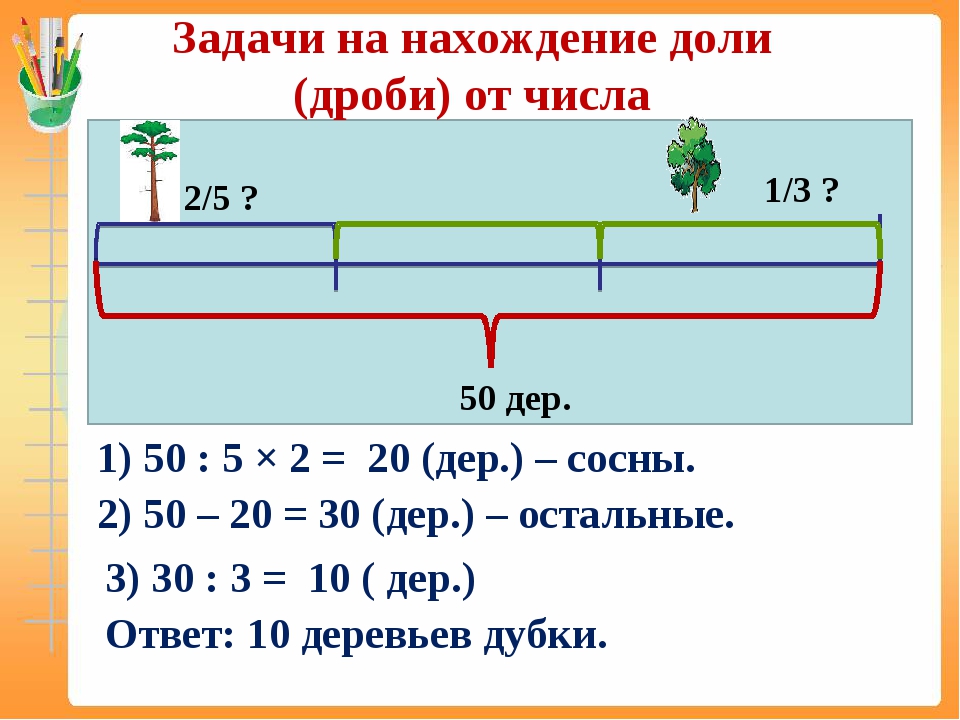Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Если у вас есть отзывы о наших математических материалах, напишите нам:

[email protected]

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

Задачи со словами

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямой и обратной вариациям

Проблемы со словами по цене за единицу

Проблемы со словами по скорости единицы

задачи по сравнению ставок

Преобразование обычных единиц Word задачи

Преобразование метрических единиц Word задачи

Word задачи по простому проценту

Word задачи по сложным процентам

Word задачи по типам ngles

Проблемы с дополнительными и дополнительными углами

Проблемы со словами с двойными фактами

Проблемы со словами тригонометрии

Проблемы со словами в процентах

Проблемы со словами

и Задачи

Задачи с десятичными словами

Задачи со словами на дроби

Задачи со словами на смешанные дроби

Одношаговые задачи с уравнениями со словами

Проблемы со словами с линейным неравенством

Задачи

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Проблемы со словами на возрастах

Проблемы со словами из теоремы Пифагора

Процент числового слова проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами при сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибыли и убытков

Сокращение в процентах

Сокращение в таблице времен

Сокращение времени, скорости и расстояния

Сокращение соотношения и пропорции

Область и диапазон 9000 рациональных функций

Область и диапазон рациональных функций

функции с отверстиями

График рациональных функций

График рациональных функций с отверстиями

Преобразование повторяющихся десятичных знаков в дроби

Десятичное представление рациональных чисел

Поиск корня из длинного квадрата видение

Л.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Метод CM для решения задач времени и работы

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении в степени 17 на 16

Сумма всех трехзначных чисел, кратных 6

Сумма всех трехзначных чисел, кратных 7

Сумма всех трехзначных чисел, делящихся на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

нерешенных математических задач | Сложнейшие математические задачи и уравнения

3.Гипотеза двойного простого числа

Вместе с гипотезой Гольдбаха гипотеза о простых числах является наиболее известной в математике, называемой теорией чисел, или изучением натуральных чисел и их свойств, часто с использованием простых чисел.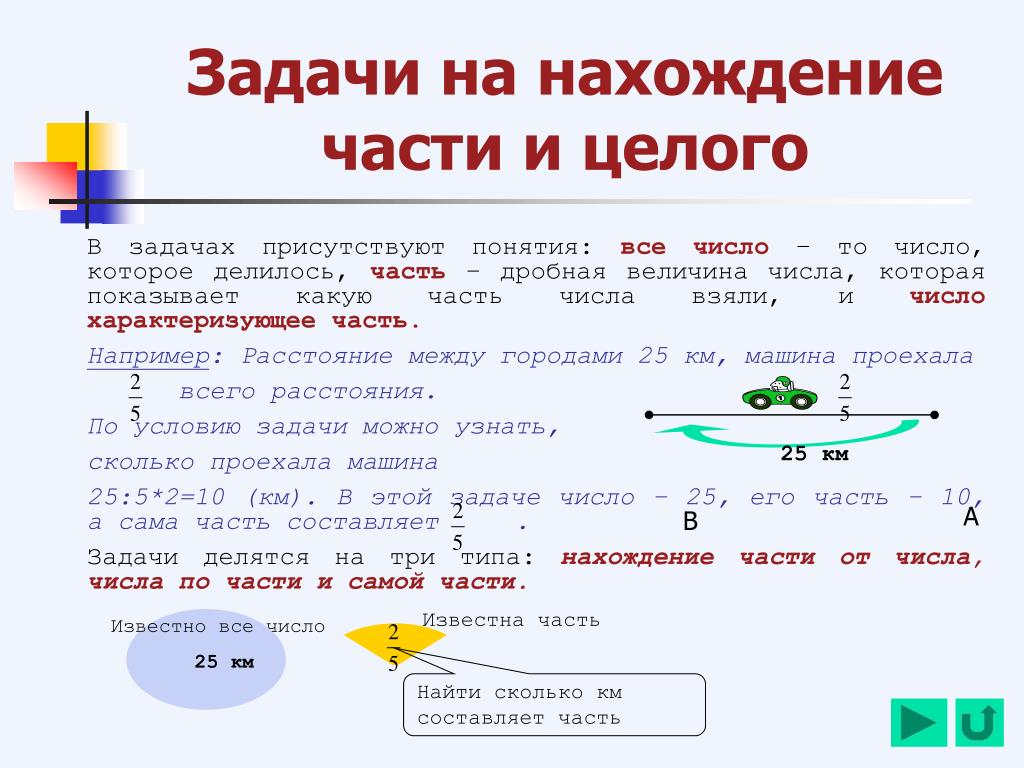Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Поскольку вы знаете эти числа с начальной школы, высказывать предположения легко.

Когда два простых числа имеют разность, равную 2, они называются простыми числами-близнецами. Итак, 11 и 13 — простые числа-близнецы, как и 599 и 601. Итак, из теории чисел первого дня известно, что существует бесконечно много простых чисел.Итак, существует ли бесконечно много близнецов простых чисел ? Гипотеза Twin Prime говорит «да».

Пойдем немного глубже. Первое в паре простых чисел-близнецов, за одним исключением, всегда на 1 меньше кратного 6. Итак, второе простое число-близнец всегда на 1 больше, чем кратное 6. Вы можете понять, почему, если вы готовы следуйте теории чисел.

Все простые числа после 2 нечетны. Четные числа всегда на 0, 2 или 4 больше, чем кратные 6, а нечетные числа всегда на 1, 3 или 5 больше, чем кратные 6.Что ж, одна из этих трех возможностей для нечетных чисел вызывает проблему. Если число на 3 больше, чем кратное 6, то оно имеет множитель 3. Наличие множителя 3 означает, что число не является простым (за единственным исключением самого 3).Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Вот почему каждое третье нечетное число не может быть простым.

Как ваша голова после этого абзаца? А теперь представьте головную боль каждого, кто пытался решить эту проблему за последние 170 лет.

Хорошая новость заключается в том, что за последнее десятилетие мы добились многообещающего прогресса.Математикам удавалось подходить к все более и более близким версиям гипотезы двойных простых чисел. Это была их идея: проблема с доказательством того, что существует бесконечно много простых чисел с разницей в 2? Как насчет доказательства того, что существует бесконечно много простых чисел с разницей в 70 000 000? Это было хорошо доказано в 2013 году Итангом Чжаном из Университета Нью-Гэмпшира.

За последние шесть лет математики улучшили это число в доказательстве Чжана с миллионов до сотен. Уменьшение числа до 2 и будет решением гипотезы о простом близнеце.Самое близкое, что мы подошли — с учетом некоторых тонких технических предположений — это 6. Время покажет, не за горами ли последний шаг от 6 до 2 или эта последняя часть бросит вызов математикам еще на десятилетия.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Математических задач и решений для целых чисел

Задачи с решениями

Задача 1: Найдите два последовательных целых числа, сумма которых равна 129.

Решение проблемы 1:
Пусть x и x + 1 (последовательные целые числа отличаются на 1) — два числа.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Используйте тот факт, что их сумма равна 129, чтобы написать уравнение
x + (x + 1) = 129
Решите относительно x, чтобы получить
x = 64
Два числа:
x = 64 и x + 1 = 65
Мы видим, что сумма двух чисел составляет 129.

Задача 2: Найдите три последовательных целых числа, сумма которых равна 366.

Решение проблемы 2:
Пусть три числа будут x, x + 1 и x + 2.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи их сумма равна 366, следовательно,
x + ( x + 1) + (x + 2) = 366
Решите относительно x и найдите три числа
x = 121, x + 1 = 122 и x + 2 = 123

Задача 3: Сумма трех последовательных четных целых чисел равна 84.Найдите числа.

Решение проблемы 3:
Разница между двумя четными целыми числами равна 2.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Пусть x, x + 2 и x + 4 — это три числа. Их сумма равна 84, следовательно
x + (x + 2) + (x + 4) = 84
Решите относительно x и найдите три числа:
x = 26, x + 2 = 28 и x + 4 = 30
. Три числа четные. Убедитесь, что их сумма равна 84.

Задача 4: Сумма нечетного целого и дважды его последовательного равна 3757.Найдите номер.

Решение проблемы 4:
Разница между двумя нечетными целыми числами равна 2.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи пусть x будет нечетным целым числом, а x + 2 будет последовательным. Сумма x и удвоения его подряд равна 3757 дает уравнение вида
x + 2 (x + 2) = 3757
Решите относительно x
x = 1251
Убедитесь, что сумма 1251 и 2 (1251 + 2 ) равно 3757.

Задача 5: Сумма первого и третьего из трех последовательных нечетных целых чисел на 131 меньше второго целого числа в три раза.Найдите три целых числа.

Решение проблемы 5:
Пусть x, x + 2 и x + 4 — три целых числа.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Сумма первого x и третьего x + 4 равна
x + (x + 4)
131 меньше трехкратного второго 3 (x + 2) дает
3 (x + 2) — 131
» Сумма первого и третьего на 131 меньше трехкратного второго «дает
x + (x + 4) = 3 (x + 2) — 131
Решите относительно x и найдите все три числа
x = 129, x + 2 = 131, x + 4 = 133

В качестве упражнения проверьте, что сумма первого и третьего на 131 меньше трехкратного

Задача 6: Произведение двух последовательных нечетных целых чисел равно 675.Найдите два целых числа.


Пусть x, x + 2 — два целых числа. Их произведение равно 144
x (x + 2) = 675
Разверните, чтобы получить квадратное уравнение.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи
x 2 + 2 x — 675 = 0
Решите относительно x, чтобы получить два решения
x = 25 или x = -27
, если x = 25, то x + 2 = 27
, если x = -27, то x + 2 = -25
У нас есть два решения. Два числа:
25 и 27 или
-27 и -25
Убедитесь, что в обоих случаях произведение равно 675.

Проблема 7: Найдите четыре последовательных четных целых числа так, чтобы сумма первых двух, добавленная к удвоенной сумме двух последних, была равна 742.

Решение проблемы 7:
Пусть x, x + 2, x + 4 и x + 6 — четыре целых числа.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Сумма первых двух
x + (x + 2)
, удвоенная сумма двух последних, записывается как
2 ((x + 4) + (x + 6)) = 4 x + 20
сумма первых двух два, сложенные с удвоением, сумма последних двух равна 742 записывается как
x + (x + 2) + 4 x + 20 = 742
Решите относительно x и найдите все четыре числа
x = 120, x + 2 = 122, x + 4 = 124, x + 6 = 126
В качестве упражнения проверьте, что сумма первых двух, добавленная к удвоенной сумме двух последних, равна 742

Задача 8: Когда наименьшее из трех последовательных нечетных целых чисел складывается с четырехкратным наибольшим, получается результат 729, превышающий среднее целое число более чем в четыре раза.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Найдите числа и проверьте свой ответ.

Решение проблемы 8:
Пусть x, x + 2 и x + 4 будут тремя целыми числами. «Наименьшее, добавленное к четырехкратному наибольшему числу, записывается следующим образом:«
x + 4 (x + 4)
»729 более чем в четыре раза больше среднего целого числа» записывается следующим образом:
729 + 4 (x + 2)
«Когда наименьшее добавляется к четырехкратному наибольшему, получается результат 729 более чем в четыре раза больше среднего «записывается следующим образом:
x + 4 (x + 4) = 729 + 4 (x + 2)
Решите относительно x и найдите все три числа
x + 4 x + 16 = 729 + 4 x + 8
x = 721
x + 2 = 723
x + 4 = 725
Проверить: наименьшее добавляется к четырехкратному наибольшему
721 + 4 * 725 = 3621
в четыре раза больше среднего
4 723 = 2892
3621 больше 2892 на
3621 — 2892 = 729

Ответ на задачу правильный.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи

Больше математических задач с подробными решениями на этом сайте. Нумерация

— Числовые математические задачи — Нумерация TeX

— Числовые математические задачи — TeX — LaTeX Stack Exchange
Сеть обмена стеков

Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange
  2. 0
  3. +0
  6. Авторизоваться Подписаться

TeX — LaTeX Stack Exchange — это сайт вопросов и ответов для пользователей TeX, LaTeX, ConTeXt и родственных систем набора.Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил

Просмотрено 10к раз

Итак, я пытаюсь напечатать свое домашнее задание по математике, и мне интересно, как пронумеровать задачи (НЕ УРАВНЕНИЯ!).Задачи на числа: Задачи ЕГЭ на числа и их свойства. Подготовительные задачи Так что я должен быть как

  4,3
//работай
4.4
//работай
5.2
//работай
6.1
//работай

Кто-нибудь знает, как это сделать?

Создан 24 янв.

Ричард Ричард

47322 золотых знака44 серебряных знака88 бронзовых знаков

4

Вы можете просто использовать \ section * и пронумеровать их в соответствии с вашими требованиями вручную:

  \ documentclass {article}
\ begin {document}
\ section * {4.3 Некоторые вещи}
// работай
\ section * {4.4 Другой раздел}
// работай
\ section * {5.2 Интересное}
// работай
\ section * {6.1 Заключительный раздел}
// работай
\ конец {документ}

You May Also Like

Leave a Reply