Разное

Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам

04.07.2021

Содержание

Таблица факториалов натуральных чисел n от 1 до 100

Факториал натурального числа n (обозначение – “n!“) равен произведению всех натуральных чисел от 1 до n включительно.

n! = 1 * 2 * 3 * 4 … * n

Ниже представлены таблицы с факториалами чисел от 1 до 20 (точные значения) и от 21 до 100 (приближенные значения).

1. Факториалы чисел от 1 до 20

Факториал числа n
(n!)		Значение
1!
1
2!2
3!6
4!24
5!120
6!720
7!5040
8!		40320
9!362880
10!3628800
11!		39916800
12!479001600
13!6227020800
14!		87178291200
15!1307674368000
16!20922789888000
17!		355687428096000
18!6402373705728000
19!121645100408832000
20!2432902008176640000

microexcel.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам ru

2. Факториалы чисел от 21 до 100

Факториал – это быстрорастущая функция, и начиная с определенного n значения достаточно велики. Поэтому в математических вычислениях удобнее пользоваться приближенными значениями для больших чисел.

Факториал числа n
(n!)
Приближенное значение
21!5,10909 ⋅ 1019
22!1,124 ⋅ 10
21
23!2,5852 ⋅ 1022
24!6,20448 ⋅ 1023
25!1,55112 ⋅ 1025
26!4,03291 ⋅ 1026
27!1,08889 ⋅ 1028
28!3,04888 ⋅ 1029
29!8,84176 ⋅ 1030
30!2,65253 ⋅ 1032
31!8,22284 ⋅ 1033
32!2,63131 ⋅ 1035
33!8,68332 ⋅ 1036
34!2,95233 ⋅ 1038
35!1,03331 ⋅ 1040
36!3,71993 ⋅ 1041
37!1,37638 ⋅ 1043
38!5,23023 ⋅ 1044
39!2,03979 ⋅ 1046
40!8,15915 ⋅ 1047
41!3,34525 ⋅ 1049
42!1,40501 ⋅ 1051
43!6,04153 ⋅ 1052
44!2,65827 ⋅ 1054
45!1,19622 ⋅ 1056
46!5,50262 ⋅ 1057
47!2,58623 ⋅ 1059
48!1,24139 ⋅ 1061
49!6,08282 ⋅ 1062
50!3,04141 ⋅ 1064
51!1,55112 ⋅ 1066
52!8,06582 ⋅ 1067
53!4,27488 ⋅ 1069
54!2,30844 ⋅ 1071
55!1,26964 ⋅ 1073
56!7,10999 ⋅ 1074
57!4,05269 ⋅ 1076
58!2,35056 ⋅ 1078
59!1,38683 ⋅ 1080
60!8,32099 ⋅ 1081
61!5,0758 ⋅ 1083
62!3,147 ⋅ 1085
63!1,98261 ⋅ 1087
64!1,26887 ⋅ 1089
65!8,24765 ⋅ 1090
66!5,44345 ⋅ 1092
67!3,64711 ⋅ 1094
68!2,48004 ⋅ 1096
69!1,71122 ⋅ 1098
70!1,1979 ⋅ 10100
71!8,5048 ⋅ 10101
72!6,1234 ⋅ 10103
73!4,4701 ⋅ 10105
74!3,3079 ⋅ 10107
75!2,4809 ⋅ 10109
76!1,8855 ⋅ 10111
77!1,4518 ⋅ 10113
78!1,1324 ⋅ 10115
79!8,9462 ⋅ 10116
80!7,1569 ⋅ 10118
81!5,7971 ⋅ 10120
82!4,7536 ⋅ 10122
83!3,9455 ⋅ 10124
84!3,3142 ⋅ 10126
85!2,8171 ⋅ 10128
86!2,4227 ⋅ 10130
87!2,1078 ⋅ 10132
88!1,8548 ⋅ 10134
89!1,6508 ⋅ 10136
90!1,4857 ⋅ 10138
91!1,352 ⋅ 10140
92!1,2438 ⋅ 10142
93!1,1568 ⋅ 10144
94!1,0874 ⋅ 10146
95!1,033 ⋅ 10148
96!9,9168 ⋅ 10149
97!9,6193 ⋅ 10151
98!9,4269 ⋅ 10153
99!9,3326 ⋅ 10155
100!9,3326 ⋅ 10157

microexcel.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам ru

Всего лишь степени двойки

И. Акулич
«Квант» №2, 2012

Давайте рассмотрим последовательность чисел, первое из которых равно 1, а каждое последующее вдвое больше: 1, 2, 4, 8, 16, … Используя показатели степени, ее можно записать в эквивалентном виде: 20, 21, 22, 23, 24, … Называется она вполне ожидаемо: последовательность степеней двойки. Казалось бы, ничего выдающегося в ней нет — последовательность как последовательность, не лучше и не хуже других. Тем не менее, она обладает весьма примечательными свойствами.

Несомненно, многие читатели встречали ее в классической истории об изобретателе шахмат, который попросил у правителя в награду за первую клетку шахматной доски одно пшеничное зерно, за вторую — два, за третью — четыре, и так далее, всё время удваивая число зерен. Понятно, что суммарное их количество равно

S = 20 + 21 + 22 + 23 + 24 + … + 263. (1)

Но так как эта сумма неимоверно велика и во много раз превосходит годовой урожай зерновых по всему миру, вышло, что мудрец ободрал правителя как липку.1

Однако зададимся сейчас другим вопросом: как с наименьшими затратами труда подсчитать величину S? Обладатели калькулятора (или, паче того, компьютера) вполне могут за обозримое время выполнить перемножения, а затем сложить полученные 64 числа, получив ответ: 18 446 744 073 709 551 615. А поскольку объем вычислений немалый, то и вероятность ошибки весьма велика.

Кто похитрей, могут углядеть в этой последовательности геометрическую прогрессию. Не знакомые же с этим понятием (или те, кто попросту забыл стандартную формулу суммы геометрической прогрессии) могут использовать следующие рассуждения. Давайте-ка умножим обе части равенства (1) на 2. Так как при удвоении степени двойки ее показатель увеличивается на 1, то получим

2S = 21 + 22 + 23 + 24 + .Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам .. + 264. (2)

Теперь из (2) вычтем (1). В левой части, понятное дело, получится 2S – S = S. В правой же части произойдет массовое взаимное уничтожение почти всех степеней двойки — от 21 до 263 включительно, и останется лишь 264 – 20 = 264 – 1. Итак:

S = 264 – 1.

Что ж, выражение заметно упростилось, и теперь, имея калькулятор, позволяющий возводить в степень, можно найти значение этой величины без малейших проблем.

А если и калькулятора нет — как быть? Перемножать в столбик 64 двойки? Еще чего не хватало! Опытный инженер или математик-прикладник, для которого главный фактор — время, сумел бы быстро оценить ответ, т.е. найти его приближенно с приемлемой точностью. Как правило, в быту (да и в большинстве естественных наук) вполне допустима погрешность в 2–3%, а если она не превосходит 1% — то это просто великолепно! Оказывается, подсчитать наши зерна с такой погрешностью можно вообще без калькулятора, и всего за несколько минут. Как? Сейчас увидите.

Итак, надо возможно точней найти произведение 64 двоек (единицу в силу ее ничтожности отбросим сразу). Разобьем их на отдельную группу из 4 двоек и еще на 6 групп по 10 двоек. Произведение двоек в отдельной группе равно 24 = 16. А произведение 10 двоек в каждой из остальных групп равно 210 = 1024 (убедитесь, кто сомневается!). Но 1024 — это около 1000, т.е. 103. Поэтому S должно быть близко к произведению числа 16 на 6 чисел, каждое из которых равно 103, т.е. S ≈ 16·1018 (ибо 18 = 3·6). Правда, погрешность здесь все же великовата: ведь 6 раз при замене 1024 на 1000 мы ошибались в 1,024 раза, а всего мы ошиблись, как легко видеть, в 1,0246 раз. Так что теперь — дополнительно перемножать 1,024 шесть раз само на себя? Нет уж, обойдемся! Известно, что для числа х, которое во много раз меньше 1, с высокой точностью справедлива следующая приближенная формула: (1 + x)n ≈ 1 + xn.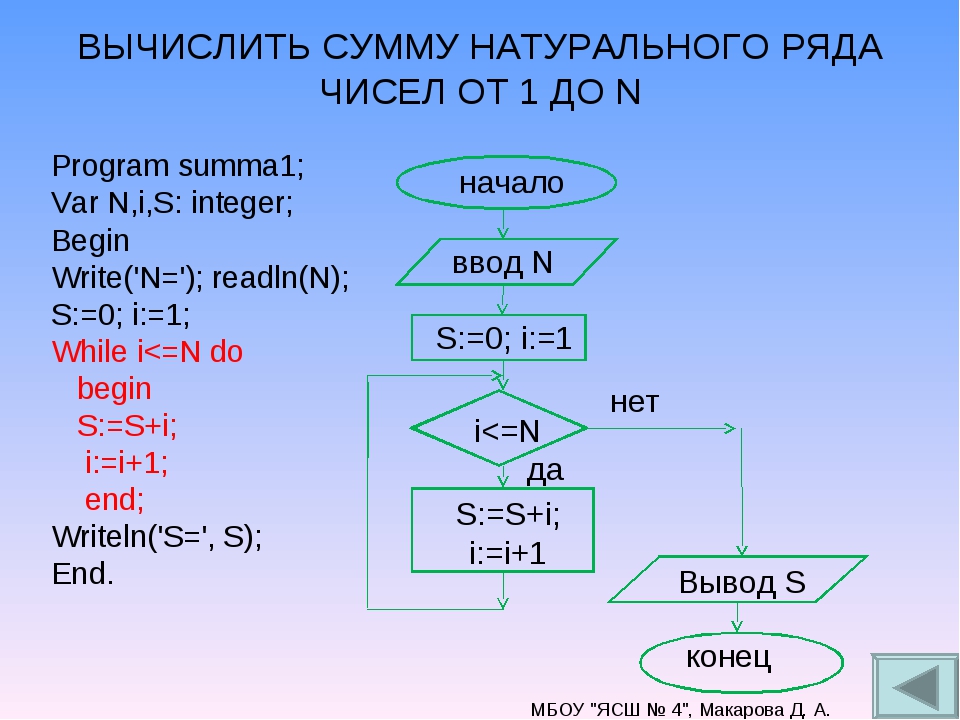Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам

Поэтому 1,0246 = (1 + 0,24)6 ≈ 1 + 0,24·6 = 1,144. Посему надо найденное нами число 16·1018 умножить на число 1,144, в результате чего получится 18 304 000 000 000 000 000, а это отличается от правильного ответа менее чем на 1%. Чего мы и добивались!

В данном случае нам крупно повезло: одна из степеней двойки (а именно — десятая) оказалась весьма близка к одной из степеней десятки (а именно — третьей). Это позволяет нам быстро оценивать значение любой степени двойки, не обязательно 64-й. Среди степеней других чисел подобное встречается нечасто. Например, 510 отличается от 107 также в 1,024 раза, но… в меньшую сторону.2 Впрочем, это того же поля ягода: поскольку 210·510 = 1010, то во сколько раз 210превосходит 103, во столько же раз 510меньше, чем 107.

Другая интересная особенность рассматриваемой последовательности заключается в том, что любое натуральное число можно построить из различных степеней двойки, причем единственным способом. Например, для номера текущего года имеем

2012 = 22 + 23 + 24 + 26 + 27 + 28 + 29 + 210.

Доказать эти возможность и единственность не составляет особого труда. Начнем с возможности. Пусть нам надо представить в виде суммы различных степеней двойки некоторое натуральное число N. Сначала запишем его в виде суммы N единиц. Так как единица — это 20, то первоначально N есть сумма одинаковых степеней двойки. Затем начнем объединять их по парам. Сумма двух чисел, равных 20, — это 21, так что в результате получится заведомо меньшее количество слагаемых, равных 21, и, возможно, одно число 20, если ему не нашлось пары. Далее попарно объединяем одинаковые слагаемые 21, получая еще меньшее количество чисел 22 (здесь тоже возможно появление непарной степени двойки 21).Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам Затем снова объединяем равные слагаемые попарно, и так далее. Рано или поздно процесс завершится, ибо количество одинаковых степеней двойки после каждого объединения уменьшается. Когда оно станет равным 1 — дело кончено. Осталось сложить все получившиеся непарные степени двойки — и представление готово.

Что касается доказательства единственности представления, то здесь хорошо подходит метод «от противного». Пусть одно и то же число N удалось представить в виде двух наборов различных степеней двойки, которые не полностью совпадают (т. е. имеются степени двойки, входящие в один набор, но не входящие в другой, и наоборот). Для начала отбросим все совпадающие степени двойки из обоих наборов (если таковые имеются). Получатся два представления одного и того же числа (меньшего или равного N) в виде суммы различных степеней двойки, причем все степени в представлениях различны. В каждом из представлений выделим наибольшую степень. В силу изложенного выше, для двух представлений эти степени различны. То представление, для которого эта степень больше, назовем первым, другое — вторым. Итак, пусть в первом представлении наибольшая степень равна 2m, тогда во втором она, очевидно, не превышает 2m–1. Но поскольку (и мы с этим уже сталкивались выше, подсчитывая зерна на шахматной доске) справедливо равенство

2m = (2m–1 + 2m–2 + … + 20) + 1,

то 2m строго больше суммы всех степеней двойки, не превосходящих 2m–1. По этой причине уже наибольшая степень двойки, входящая в первое представление, наверняка больше суммы всех степеней двойки, входящих во второе представление. Противоречие!

Фактически мы только что обосновали возможность записи чисел в двоичной системе счисления.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам Как известно, в ней используются лишь две цифры — ноль и единица, и каждое натуральное число записывается в двоичной системе единственным способом (например, упомянутое выше 2012 — как 11 111 011 100). Если пронумеровать разряды (двоичные цифры) справа налево, начиная с нуля, то номера тех разрядов, в которых стоят единицы, как раз и будут показателями степеней двоек, входящих в представление.3

Менее известно следующее свойство множества целых неотрицательных степеней двойки. Давайте некоторым из них произвольным образом присвоим знак «минус», т. е. из положительных сделаем отрицательными. Единственное требование — чтобы в результате и положительных, и отрицательных чисел оказалось бесконечное количество. Например, можно присвоить знак «минус» каждой пятой степени двойки или, допустим, оставить положительными только числа 210, 2100, 21000, и так далее — вариантов здесь сколько угодно.

Как ни удивительно, но любое целое число можно (и притом единственным способом) представить в виде суммы различных слагаемых нашей «положительно-отрицательной» последовательности.4 И доказать это не очень-то сложно (например, индукцией по показателям степеней двоек). Главная идея доказательства — наличие сколь угодно больших по абсолютной величине как положительных, так и отрицательных слагаемых. Попробуйте выполнить доказательство сами.

Интересно понаблюдать за последними цифрами членов последовательности степеней двойки. Так как каждое последующее число последовательности получается удвоением предыдущего, то последняя цифра каждого из них полностью определяется последней цифрой предыдущего числа. А так как различных цифр ограниченное количество, последовательность последних цифр степеней двойки просто обязана быть периодической! Длина периода, естественно, не превышает 10 (поскольку именно столько цифр мы используем), но это сильно завышенное значение. Попробуем оценить его, не выписывая пока саму последовательность.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам Ясно, что последние цифры всех степеней двойки, начиная с 21, четные. Кроме того, среди них не может быть нуля — потому что число, оканчивающееся нулем, делится на 5, в чем заподозрить степени двойки никак нельзя. А так как четных цифр без нуля имеется всего четыре, то и длина периода не превосходит 4.

Проверка показывает, что так оно и есть, причем периодичность проявляется почти сразу: 1, 2, 4, 8, 6, 2, 4, 8, 6, … — в полном соответствии с теорией!

Не менее успешно можно оценить и длину периода последней пары цифр последовательности степеней двойки. Так как все степени двойки, начиная с 22, делятся на 4, то и числа, образованные их последними двумя цифрами, делятся на 4. Не более чем двузначных чисел, делящихся на 4, имеется всего 25 (для однозначных чисел предпоследней цифрой считаем ноль), но из них надо выбросить пять чисел, оканчивающихся нулем: 00, 20, 40, 60 и 80. Так что период может содержать не более 25 – 5 = 20 чисел. Проверка показывает, что так и есть, начинается период с числа 22 и содержит пары цифр: 04, 08, 16, 32, 64, 28, 56, 12, 24, 48, 96, 92, 84, 68, 36, 72, 44, 88, 76, 52, а затем опять 04 и так далее.

Аналогично можно доказать, что длина периода последних m цифр последовательности степеней двойки не превышает 4·5m–1 (более того — на самом деле она равна 4·5m–1, но доказать это значительно сложнее).

Итак, на последние цифры степеней двойки наложены довольно жесткие ограничения. А как насчет первых цифр? Здесь ситуация практически противоположная. Оказывается, для любого набора цифр (первая из которых — не ноль) найдется степень двойки, начинающаяся с этого набора цифр. И таких степеней двойки бесконечно много! Например, существует бесконечное количество степеней двойки, начинающихся с цифр 2012 или, скажем, 3 333 333 333 333 333 333 333.

А если рассмотреть только одну самую первую цифру различных степеней двойки — какие значения она может принимать? Нетрудно убедиться, что любые — от 1 до 9 включительно (нуля среди них, естественно, нет).Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам Но какие из них встречаются чаще, а какие реже? Как-то сразу не видно причин, по которым одна цифра должна встречаться чаще другой. Однако более глубокие размышления показывают, что как раз равной встречаемости цифр ожидать не приходится. Действительно, если первая цифра какой-либо степени двойки есть 5, 6, 7, 8 или 9, то первая цифра следующей за ней степени двойки будет обязательно единицей! Поэтому должен иметь место «перекос», по крайней мере, в сторону единицы. Следовательно, вряд ли и остальные цифры будут «равнопредставленными».

Практика (а именно — прямой компьютерный расчет для первых нескольких десятков тысяч степеней двойки) подтверждает наши подозрения. Вот какова относительная доля первых цифр степеней двойки с округлением до 4 знаков после запятой:

1 — 0,3010
2 — 0,1761
3 — 0,1249
4 — 0,0969
5 — 0,0792
6 — 0,0669
7 — 0,0580
8 — 0,0512
9 — 0,0458

Как видим, с ростом цифр эта величина убывает (и потому та же единица примерно в 6,5 раз чаще бывает первой цифрой степеней двойки, чем девятка). Как ни покажется странным, но практически такое же соотношение количеств первых цифр будет иметь место почти для любой последовательности степеней — не только двойки, но, скажем, и тройки, пятерки, восьмерки и вообще почти любого числа, в том числе и нецелого (исключение составляют лишь некоторые «особые» числа). Причины этого весьма глубоки и непросты, и для их уяснения надо знать логарифмы. Для тех, кто с ними знаком, приоткроем завесу: оказывается, относительная доля степеней двойки 5, десятичная запись которых начинается с цифры F (для F = 1, 2, …, 9), составляет lg (F + 1) – lg (F), где lg — так называемый десятичный логарифм, равный показателю степени, в которую надо возвести число 10, чтобы получить число, стоящее под знаком логарифма.6

Используя упомянутую выше связь между степенями двойки и пятерки, А. Канель обнаружил интересное явление.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам Давайте из последовательности первых цифр степеней двойки (1, 2, 4, 8, 1, 3, 6, 1, 2, 5, …) выберем несколько цифр подряд и запишем их в обратном порядке. Оказывается, эти цифры непременно встретятся тоже подряд, начиная с некоторого места, в последовательности первых цифр степеней пятерки.7

Степени двойки также являются своеобразным «генератором» для производства широко известных совершенных чисел, которые равны сумме всех своих делителей, за исключением себя самого. Например, у числа 6 четыре делителя: 1, 2, 3 и 6. Отбросим тот, который равен самому числу 6. Осталось три делителя, сумма которых как раз равна 1 + 2 + 3 = 6. Поэтому 6 — совершенное число.

Для получения совершенного числа возьмем две последовательные степени двойки: 2n–1 и 2n. Уменьшим большую из них на 1, получим 2n – 1. Оказывается, если это — простое число, то, домножив его на предыдущую степень двойки, мы образуем совершенное число 2n–1 (2n – 1). Например, при п = 3 получаем исходные числа 4 и 8. Так как 8 – 1 = 7 — простое число, то 4·7 = 28 — совершенное число.8 Более того — в свое время Леонард Эйлер доказал, что все четные совершенные числа имеют именно такой вид. Нечетные совершенные числа пока не обнаружены (и мало кто верит в их существование).

Тесную связь имеют степени двойки с так называемыми числами Каталана, последовательность которых имеет вид 1, 1, 2, 5, 14, 42, 132, 429… Они часто возникают при решении различных комбинаторных задач. Например, сколькими способами можно разбить выпуклый n-угольник на треугольники непересекающимися диагоналями? Всё тот же Эйлер выяснил, что это значение равно (n – 1)-му числу Каталана (обозначим его Kn–1), и он же выяснил, что Kn = Kn–1·(4n – 6)/n. Последовательность чисел Каталана имеет множество любопытных свойств, и одно из них (как раз связанное с темой этой статьи) заключается в том, что порядковые номера всех нечетных чисел Каталана являются степенями двойки!

Степени двойки нередко встречаются в различных задачах, причем не только в условиях, но и в ответах.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам Возьмем, например, популярную когда-то (да и поныне не забытую) Ханойскую башню. Так называлась игра-головоломка, придуманная в XIX веке французским математиком Э. Люка. Она содержит три стержня, на один из которых надето n дисков с отверстием в середине каждого. Диаметры всех дисков различны, и они расположены в порядке убывания снизу вверх, т. е. самый большой диск — внизу (см. рисунок). Получилась как бы башня из дисков.

Требуется перенести эту башню на другой стержень, соблюдая такие правила: перекладывать диски строго по одному (снимая верхний диск с любого стержня) и всегда класть только меньший диск на больший, но не наоборот. Спрашивается: какое наименьшее число ходов для этого потребуется? (Ходом мы называем снятие диска с одного стержня и надевание его на другой.) Ответ: оно равно 2n – 1, что легко доказывается по индукции.

Пусть для n дисков потребное наименьшее число ходов равно Xn. Найдем Xn+1. В процессе работы рано или поздно придется снимать самый большой диск со стержня, на который первоначально были надеты все диски. Так как этот диск можно надевать только на пустой стержень (иначе он «придавит» меньший диск, что запрещено), то все верхние n дисков придется предварительно перенести на третий стержень. Для этого потребуется не меньше Xn ходов. Далее переносим наибольший диск на пустой стержень — вот еще один ход. Наконец, чтобы сверху его «притиснуть» меньшими n дисками, опять потребуется не меньше Xn ходов. Итак, Xn+1 ≥ Xn + 1 + Xn = 2Xn + 1. С другой стороны, описанные выше действия показывают, как можно справиться с задачей именно 2Xn + 1 ходами. Поэтому окончательно Xn+1 =2Xn + 1. Получено рекуррентное соотношение, но для того чтобы его привести к «нормальному» виду, надо еще найти X1.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам Ну, это проще простого: X1 = 1 (меньше просто не бывает!). Не составляет труда, основываясь на этих данных, выяснить, что Xn = 2n – 1.

Вот еще одна интересная задача:

Найдите все натуральные числа, которые нельзя представить в виде суммы нескольких (не менее двух) последовательных натуральных чисел.

Давайте проверим сначала наименьшие числа. Ясно, что число 1 в указанном виде непредставимо. Зато все нечетные, которые больше 1, представить, конечно, можно. В самом деле, любое нечетное число, большее 1, можно записать как 2k + 1 (k — натуральное), что есть сумма двух последовательных натуральных чисел: 2k + 1 = k + (k + 1).

А как обстоят дела с четными числами? Легко убедиться, что числа 2 и 4 нельзя представить в требуемом виде. Может, и для всех четных чисел так? Увы, следующее же четное число опровергает наше предположение: 6 = 1 + 2 + 3. Зато число 8 опять не поддается. Правда, следующие числа вновь уступают натиску: 10 = 1 + 2 + 3 + 4, 12 = 3 + 4 + 5, 14 = 2 + 3 + 4 + 5, а вот 16 — вновь непредставимо.

Что ж, накопленная информация позволяет сделать предварительные выводы. Обратите внимание: не удалось представить в указанном виде только степени двойки. Верно ли это для остальных чисел? Оказывается, да! В самом деле, рассмотрим сумму всех натуральных чисел от m до n включительно. Так как всего их, по условию, не меньше двух, то n > m. Как известно, сумма последовательных членов арифметической прогрессии (а ведь именно с ней мы имеем дело!) равна произведению полусуммы первого и последнего членов на их количество. Полусумма равна (n + m)/2, а количество чисел равно n – m + 1. Поэтому сумма равна (n + m)(n – m + 1)/2. Заметим, что в числителе находятся два сомножителя, каждый из которых строго больше 1, и при этом четность их — различна.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам Выходит, что сумма всех натуральных чисел от m до n включительно делится на нечетное число, большее 1, и потому не может быть степенью двойки. Так что теперь понятно, почему не удалось представить степени двойки в нужном виде.

Осталось убедиться, что не степени двойки представить можно. Что касается нечетных чисел, то с ними мы уже разобрались выше. Возьмем какое-либо четное число, не являющееся степенью двойки. Пусть наибольшая степень двойки, на которую оно делится, это 2a (a — натуральное). Тогда если число поделить на 2a, получится уже нечетное число, большее 1, которое мы запишем в знакомом виде — как 2k + 1 (k — тоже натуральное). Значит, в целом наше четное число, не являющееся степенью двойки, равно 2a (2k + 1). А теперь рассмотрим два варианта:

  1. 2a+1 > 2k + 1. Возьмем сумму 2k + 1 последовательных натуральных чисел, среднее из которых равно 2a. Легко видеть, что тогда наименьшее из них равно 2a – k, а наибольшее равно 2a + k, причем наименьшее (и, значит, все остальные) — положительное, т. е. действительно натуральное. Ну, а сумма, очевидно, составляет как раз 2a(2k + 1).
  2. 2a+1 < 2k + 1. Возьмем сумму 2a+1 последовательных натуральных чисел. Здесь нельзя указать среднее число, ибо количество чисел четное, но указать пару средних чисел можно: пусть это числа k и k + 1. Тогда наименьшее из всех чисел равно k + 1 – 2a (и тоже положительное!), а наибольшее равно k + 2a. Сумма их тоже равна 2a(2k + 1).

Вот и всё. Итак, ответ: непредставимые числа — это степени двойки, и только они.

А вот еще одна задача (впервые ее предложил В.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам  Произволов, но в несколько иной формулировке):

Садовый участок окружен сплошным забором из N досок. Согласно приказу тети Полли Том Сойер белит забор, но по собственной системе: продвигаясь всё время по часовой стрелке, сначала белит произвольную доску, затем пропускает одну доску и белит следующую, затем пропускает две доски и белит следующую, затем пропускает три доски и белит следующую, и так далее, каждый раз пропуская на одну доску больше (при этом некоторые доски могут быть побелены несколько раз — Тома это не смущает).

Том считает, что при такой схеме рано или поздно все доски будут побелены, а тетя Полли уверена, что хотя бы одна доска останется непобеленной, сколько бы Том ни работал. При каких N прав Том, а при каких — тетя Полли?

Описанная система побелки представляется довольно хаотичной, поэтому первоначально может показаться, что для любого (или почти любого) N каждой доске когда-нибудь достанется своя доля известки, т. е., в основном, прав Том. Но первое впечатление обманчиво, потому что на самом деле Том прав только для значений N, являющихся степенями двойки. Для остальных N найдется доска, которая так и останется навеки непобеленной. Доказательство этого факта довольно громоздко (хотя, в принципе, несложно). Предлагаем читателю выполнить его самому.

Вот каковы они — степени двойки. С виду — проще простого, а как копнешь… И затронули мы здесь далеко не все удивительные и загадочные свойства этой последовательности, а лишь те, что бросились в глаза. Ну, а читателю предоставляется право самостоятельно продолжить исследования в этой области. Несомненно, они окажутся плодотворными.

1 Впрочем, действительно ли правитель согласился выплатить требуемое, история умалчивает. Более вероятно, что для мудреца все закончилось длительным тюремным заключением по статье «за наглость».
2 Для любопытных вот еще одно хорошее совпадение: 69 = 10 077 696, в котором относительное расхождение с ближайшей степенью десятки всего около 0,8%, что примерно втрое меньше, чем для 210.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам
3 Повсеместно используемая десятичная система устроена по такому же принципу. Только вместо степеней двойки используются степени десятки (потому она так и называется), а цифры в записи показывают, в каком количестве очередную степень десятки надо прибавлять.
4 При этом число 0 (ноль) представляется как полное отсутствие слагаемых (т.е., формально говоря, нулевое их количество).
5 И не только двойки, как было отмечено ранее!
6 Жаждущие подробностей могут прочесть статью В. Болтянского «Часто ли степени двойки начинаются с единицы?» («Квант» №5 за 1978 г.), а также статью В. Арнольда «Статистика первых цифр степеней двойки и передел мира» («Квант» №1 за 1998 г.).
7 См. задачу М1599 из «Задачника «Кванта» («Квант» №6 за 1997 г.).
8 В настоящее время известны 43 совершенных числа, наибольшее из которых равно 230402456(230402457 – 1). Оно содержит свыше 18 миллионов цифр.

Правильные ответы к игре Выбирайка в Одноклассниках: эпизод 6 уровни 151-180

А мы снова возвращаемся к прохождению приложений из социальных сетей и продолжаем составлять правильные ответы к игре Выбирайка (ну логично, неверные ответы нам совсем ни к чему).
Впереди ещё Вас ждёт множество картинок с заданиями, в которых из двух предложенных вариантов необходимо выбрать один правильный ответ. Помните, что за каждые верно решённые 5 заданий — Вы в подарок получите 1 энергию, которая поможет обогнать друзей 🙂

Игра «Выбирайка» — ответы на эпизод 6 «Небеса»

Выбирайка: Уровень 151
Вопрос: Куда не следует ходить, если боишься волков?
Варианты решения: В лес или в баню.
Ответ: волков бояться — в лес не ходить.
Выбирайка: Уровень 152
Вопрос: Чему равна сумма чисел от 0 до 100 включительно?
Варианты решения: 9090 или 5050.
Ответ: 5050.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам
Выбирайка: Уровень 153
Вопрос: Какому писателю принадлежат слова «Тот, кто любит, должен разделять участь того, кого он любит»?
Варианты решения: Булгаков или Тургенев.
Ответ: Булгаков.
Выбирайка: Уровень 154
Вопрос: Что называют черным золотом, чёрную игру или нефть?
Ответ: Нефть.
Выбирайка: Уровень 155
Вопрос: Кто гонялся за героями фильма «Невероятные приключения итальянцев в России»?
Варианты решения: Лев или Тигр.
Ответ: Лев.
Выбирайка: Уровень 156
Вопрос: Кто из этих людей был писателем?
Выбирайка: Уровень 157
Вопрос: В каком океане находится самая глубокая впадина?
Варианты решения: Тихий или Индийский.
Ответ: Тихий.
Выбирайка: Уровень 158
Вопрос: Кто участвовал в создании МГУ, Петр Первый или Ломоносов?
Ответ: Ломоносов.
Выбирайка: Уровень 159
Вопрос: О чем говорят: «…как навоз – сегодня нет, а завтра – воз»?
Варианты решения: Деньги или Книги.
Ответ: Деньги.
Выбирайка: Уровень 160
Вопрос: Сочетание каких двух карт называется Марьяж?
Варианты решения: Король-Дама или Король-Туз.
Ответ: Король-Дама.
Выбирайка: Уровень 161
Вопрос: Что содержит больше калорий?
Варианты решения: Гречка или Простокваша.
Ответ: Гречка.
Выбирайка: Уровень 162
Вопрос: Как выглядит Беляк?
Выбирайка: Уровень 163
Вопрос: Куда сомотрит волк, несмотря на вполне достаточную кормежку?
Варианты решения: В лес или На небо.
Ответ: В лес.
Выбирайка: Уровень 164
Вопрос: Кто из персонажей фильма «Джентельмены удачи» советовал «ходить лошадью»?
Варианты решения: Доцент или Косой.
Ответ: Косой.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам
Выбирайка: Уровень 165
Вопрос: Кем был герой былин Мукула Селянинович, дружинник или пахарь?
Ответ: Пахарь.
Выбирайка: Уровень 166
Вопрос: Что тяжелее, пуд или центнер?
Ответ: Центнер.
Выбирайка: Уровень 167
Вопрос: Кого, согласно русским народным сказкам, пленила Марья Моревна – прекрасная королевна?
Варианты решения: Кощей или Змей Горыныч.
Ответ: Кощей.
Выбирайка: Уровень 168
Вопрос: Сколько, согласно пословице, ждут обещанного?
Варианты решения: Два месяца или Три года.
Ответ: обещанного три года ждут.
Выбирайка: Уровень 169
Вопрос: Чье стихотворение начинается с этих слов: «Зима, крестьянин, торжествуя»?
Варианты решения: Пушкин или Некрасов.
Ответ: Пушкин.
Выбирайка: Уровень 170
Вопрос: Из какого мяса традиционно готовится начинка для чебуреков?
Варианты решения: Говядина или Баранина.
Ответ: Баранина.
Выбирайка: Уровень 171
Вопрос: Каким предметом китайцы стараются не пользоваться в преддверии Нового года, чтобы не разрушить счастья?
Варианты решения: Веник или Нож.
Ответ: Нож.
Выбирайка: Уровень 172
Вопрос: Где изображен килл;ep Леон?
Выбирайка: Уровень 173
Вопрос: Какая река длинее, Нил или Амазонка?
Ответ: Амазонка.
Выбирайка: Уровень 174
Вопрос: Какой знак Зодиака следует за Стрельцом?
Варианты решения: Козерог или Близнецы.
Ответ: Козерог.
Выбирайка: Уровень 175
Вопрос: На дорогах какой страны левостороннее движение?
Варианты решения: Австралия или США.
Ответ: Австралия.
Выбирайка: Уровень 176
Вопрос: Что следует держать за зубами, язык или хлеб?
Ответ: ешь пирог с грибами, а язык держи за зубами.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам
Выбирайка: Уровень 177
Вопрос: Что тяжелее?
Варианты решения: Танк Т-34 или Трамвай.
Ответ: Трамвай.
Выбирайка: Уровень 178
Вопрос: На какой птице летала Дюймовочка?
Варианты решения: Орел или Ласточка.
Ответ: Ласточка.
Выбирайка: Уровень 179
Вопрос: Откуда появлялся всадник без головы в фильме «Сонная лощина»?
Варианты решения: Дерево Мертвых или Врата Призраков.
Ответ: Дерево Мертвых.
Выбирайка: Уровень 180
Вопрос: Как обычно называют человека, упустившего верный шанс, куртка или шляпа?
Ответ: Шляпа.

Mathematica Функции

Элементарное введение в Wolfram Language

(язык программирования системы Mathematica)

перейти к содержанию

2. Знакомство с функциями

Когда вы набираете 2+2, Wolfram Language понимает это как Plus[2,2], где Plus — это функция. В Wolfram встроено более 5000 функций, среди которых арифметические составляют лишь малую часть.

| Пока под функцией можно понимать формулу, которая имеет уникальное имя (Plus в примере выше) и в которую надо подставить данные (2,2), чтобы она могла быть вычислена.

Вычислим 3+4 с помощью функции Plus:
ln[1]:=Plus[3,4]
Out[1]=7

Вычислим 1+2+3 с помощью Plus:
ln[1]:=Plus[1,2,3]
Out[1]=6

Функция Times выполняет умножение:
ln[1]:=Times[2,3]
Out[1]=6

Вы можете помещать вызов функций в другие функции:
ln[1]:=Times[2,Plus[2,3]]
Out[1]=10

В Wolfram все функции требуют квадратные скобки []. В именах функций первая буква должна быть заглавной.

Функция Max находит максимальное (наибольшее) число из данного набора чисел.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам 2возведение в степеньMax[3,4]максимумMin[3,4]минимумRandomInteger[10]случайное целое число

Упражнения

| ответы к упражнениям приведены после условий

2.1 С помощью функции Plus вычислите 7+6+5.

2.2 Вычислите 2×(3+4) с помощью Plus и Times.

2.3 Вычислите наибольшее из чисел 6×8 и 5×9, используя функцию Max.

2.4 Получите случайное целое число от 0 до 1000 включительно.

2.5 Используйте Max и RandomInteger для генерации целого числа от 10 до 20 включительно.

х2.1 Вычислите 5×4×3×2 с помощью Times.

x2.2 Вычислите 2-3 с помощью Subtract.

x2.3 Вычислите (8+7)*(9+2), используя Times and Plus.

x2.4 Найдите значение (26-89)/9 с помощью Subtract и Divide.

x2.5 Вычислите с помощью Subtract и Power.

x2.6 Найдите наибольшее число из и

x2.7 Найдите произведение 3 и наибольшего числа из и .

x2.8 Найдите сумму двух случайных целых чисел, каждое из которых от 0 до 1000 включительно.

Ответы к упражнениям

2.1) 18
2.2) 14
2.3) 48

х2.1) 120
х2.2) -1
х2.3) 165
х2.4) -7
х2.5) 75
х2.6) 243
х2.7) 243

Вопросы и ответы

1. Обязательно ли начинать название функций Plus, RandomInteger и др. с заглавной буквы?

Да. В Wolfram plus не то же самое, что и Plus. Заглавная буква означает, что вы обращаетесь к встроенной («официальной») функции plus.

2. Обязательно ли в функции использовать именно квадратные скобки […]?

Да. Квадратные скобки […] предназначены для функций, а круглые (..) только для группировки в выражениях, например, 2*(3+4).

3. Как произносится запись Plus[2,3]?

Обычно говорят «plus двух и трех», «plus от двух и трех», иногда «plus два три». Символ «[» можно называть «открывающей скобкой», а «]» — «закрывающей скобкой».Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам

4. Почему мы использовали Plus[2,3] вместо 2+3?

Именно для Plus это было необязательно. Но для большинства других функций — таких как Max или RandomInteger — таких вариантов записи как «+» для Plus нет, поэтому вы должны использовать их имена.

5. Могу я использовать Plus[] и «+» совместно?

Да. Например, Plus[4+5,2+3] или Plus[4,5]*5.

6. Что значит красный цвет, которым Wolfram выделяет введенный мной текст?

Значит, что набранный вами текст непонятен Wolfram. Первым делом проверьте открывающие и закрывающие скобки. Подробности смотрите в главе 47.

Примечания

  • В Wolfram Language выражения (expressions) состоят из вложенных деревьев функций.
  • Функция Plus может сложить любое количество чисел. Функция Subtract от данного числа вычитает  только одно число (для исключения неоднозначности, например, (2-3)-4 и 2-(3-4) ) .
  • В Wolfram Language понятие функции шире, чем в классических математических или компьютерных науках. Например, F[что-то] является функцией вне зависимости от того, какой возращается результат после выполнения: конечный или в символической форме.

 предыдущая глава                                         следующая глава

Перевод с дополнениями: И.Колемаев

источник http://www.wolfram.com/language/elementary-introduction/02-introducing-functions.html

перейти к содержанию

 

Информатика в школе — Циклы





Календарь
Календари для ucoz

Статистика

Онлайн всего: 1

Гостей: 1

Пользователей: 0


Задачи на циклы.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам

 

  1. Напишите программу печати таблицы перевода расстояний из дюймов в сантиметры для значений длин от 1 до 20 дюймов. 1 дюйм = 2,54 см.
  2. Напишите программу вывода всех четных чисел от 2 до 100 включительно.
  3. Составьте программу, вычисляющую сумму квадратов всех чисел от 1 до N.
  4. Напишите программу, определяющую сумму всех нечетных чисел от 1 до 99.
  5. С помощью repeat напишите программу, которая требует у вас пароль, например 111. Если пароль правильный, то заполняет все строки экрана сообщением «Молодец». Если после пятой попытки пароль все равно неверен, выходит из программы.
  6. Дана не пустая последовательность, признаком окончания данной последовательности является ‘0’. Определить количество чисел и их среднеарифметическое. Для ввода данных используйте генератор случайных чисел.
  7. Составьте программу получения в порядке убывания всех делителей данного числа.
  8. Составьте программу  печати символов от a до z .
  9. Составьте программу определения наибольшего общего делителя двух натуральных чисел.
  10. Составьте программу определения наименьшего общего кратного двух натуральных чисел.
  11. Печатать символы до первого пробела.
  12. Составьте программу  печати символов от z до a .
  13. Составьте программу, подсчитывающую количество цифр вводимого вами целого неотрицательного числа. Можно использовать операцию целочисленного деления.
  14. Составьте программу, определяющую максимальное из всех вводимых вами чисел. Концом ввода чисел является введенное число 0.
  15. Найти наибольшее и наименьшее значение функции y=3×2+x-4, если на заданном интервале [a,b] Х изменяется с шагом 0,1.
  16. Вычислите сумму квадратов N четных натуральных чисел.
  17. Вычислить:  1+2+4+8+…+210
  18. Вычислить:  (1+2)*(1+2+3)*…*(1+2+…+10)
  19. В бригаде, работающей на уборке сена, имеется N косилок.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам Первая из них работала M часов, а каждая следующая на 10 минут больше, чем предыдущая. Сколько часов проработала вся бригада?
  20.  Дана не пустая последовательность, признаком окончания данной последовательности является ‘0’. Определить количество нечетных чисел и их сумму. Для ввода данных используйте генератор случайных чисел.
  21. Билет называют «счастливым», если в его номере сумма первых трех цифр равна сумме последних трех. Подсчитать число тех «счастливых» билетов, у которых сумма трех цифр равна 13. Номер билета может быть от 000000 до 999999.
  22. В ЭВМ вводятся по очереди координаты N точек. Определить, сколько из них попадает в круг радиусом R с центром в точке (a,b).
  23. В ЭВМ вводятся по очереди данные о росте N учащихся класса. Определить средний рост учащихся в классе.
  24. Составьте программу, суммирующую штрафное время команд при игре в хоккей. Выводить на экран суммарное штрафное время обеих команд после любого его изменения. После окончания игры выдать итоговое сообщение.
  25. Составьте программу вычисления степени числа A с натуральным показателем N. Записать варианты программы со всеми видами циклов: while, repeat, for.
  26. Составьте программу, вычисляющую A*B, не пользуясь операцией умножения. А и B любое натуральное число.
  27. Для заданного числа N составьте программу вычисления суммы S=1+1/2+1/3+1/4+…+1/N, где N – натуральное число.
  28. Каждая бактерия делится на две в течение одной минуты. В начальный момент имеется одна бактерия. Составьте программу, которая рассчитывает количество бактерий на заданное вами целое значение момента времени (15 минут, 7 минут и т.п.). 
  29. Составьте программу вывода на экран всех простых чисел, не превосходящих заданного N. Простым называется натуральное число больше единицы, имеющее только два делителя: единицу и само это число.
  30. В 1202г.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам Итальянский математик Леонардо Пизанский (Фибоначчи) предложил такую задачу: пара кроликов каждый месяц дает приплод – двух кроликов (самца и самку), от которых через два месяца уже получается новый приплод, Сколько кроликов будет через год, если в начале года имелась одна пара? Согласно условию задачи числа, соответствующие количеству кроликов, которые появляются через каждый месяц, составляют последовательность 1, 1, 2, 3, 5, 8, 13, 21, 37, … Составьте программу, позволяющую найти все числа Фибоначчи, меньшие заданного числа N.
  31. Составьте программу, которая выводит полную запись десятичного числа 42*4*, в которой пропущены две цифры (обозначены *), если известно, что данное число кратно 72.
  32. В старо японском календаре был принят 60-летний цикл, состоявший из пяти 12-летних подциклов. Подциклы обозначались названиями цвета: зеленый, красный, желтый, белый и черный. Внутри каждого подцикла годы носили названия животных: крысы, коровы, тигра, зайца, дракона, змеи, лошади, овцы, обезьяны, курицы, собаки и свиньи. 1984 – год зеленой крысы – был началом очередного цикла. Напишите программу, которая вводит номер некоторого года нашей эры и печатает его название по старояпонскому календарю. (4 балла)
  33. Составьте программу, которая по введенному вами числу N (от 1 до 100) напечатает все натуральные числа X русскими буквами (двадцать, сорок пять и т.д.). Например, для числа 4 программа должная напечатать «один», так как в слове «один» четыре буквы. Для числа 9 программа должная напечатать «сорок пять», так как в записи числа «сорок пять» девять букв. (7 баллов)
  34. Запишите любое число от 1 до 1000, введенное пользователем, русскими буквами. Например, 2 – два, 150 – сто пятьдесят.
  35. Найти все двузначные числа, сумма цифр которых не меняется при умножении числа на 2,3,4,5,6,7,8,9.
  36. Найти все трехзначные числа, сумма цифр которых равна данному целому числу.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам
  37. Найти все трехзначные числа, средняя цифра которых равна сумме первой и второй цифр.
  38. Найти все трехзначные числа, которые можно представить разностью между квадратом числа, образованного первыми двумя цифрами и квадратом третьей цифры.
  39. Найти все двузначные числа, сумма квадратов цифр которых делится на 17.
  40. Найти все трехзначные числа, представимые в виде сумм факториалов своих цифр.
  41. Найти двузначное число, обладающее тем свойством, что куб суммы его цифр равен квадрату самого числа.
  42. Найти двузначное число, равное утроенному произведению его цифр.
  43. В каких двузначных числах удвоенная сумма цифр равна их произведению?
  44. Можно ли заданное натуральное число М представить в виде суммы квадратов двух натуральных чисел? Написать программу решения этой задачи.

<<

                                                                                                                                                                                                                                                                                        


Праздники России





Иллюстрированный самоучитель по Basic, вводный курс › Алгоритмы, графика, символы и строки › Наращивание переменной [страница — 66] | Самоучители по программированию

Наращивание переменной

О том, что такое переменная и об операторе присваивания мы уже говорили. И обращали внимание на такое абсурдное с точки зрения математики выражение:

Х=Х+1

Применяется оно обычно в Бейсике для работы всевозможных счетчиков, а также для подсчета сумм или произведений рядов чисел.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам Например, необходимо вычислить сумму всех четных чисел от 1 до 100 включительно. Программа будет выглядеть так:

CLS S=0

Обнуление переменной, где будет накапливаться сумма:

FOR 1=2 TO 100 STEP 2
S=S+I NEXT I? "Сумма четных чисел от 1 до 100 равна"; S

Программа работает эффективно и просто. Параметром цикла являются сами четные числа, которые нам остается накапливать в переменной S. Разберем алгоритм по шагам:

  • s=0;
  • 1=2;
  • s=0+2=2;
  • 1=4;
  • s=2+4=6;
  • 1=6;
  • s=6+6 и т. д. до 100.

На экране в результате увидим надпись:

Сумма четных чисел от 1 до 100 равна 2550.

Объяснять здесь вроде больше нечего Иногда лучше решать, чем говорить. Итак, вам необходимо написать программы для нахождения сумм.

209. Всех чисел, делящихся на 13 в интервале [1; 1000].

210.

211.

212. Напишите программу для нахождения суммы пяти произвольных чисел, вводимых с клавиатуры (сумматор).

213. Создайте программу для нахождения суммы пяти заданных чисел, указанных в операторе data.

214. Напишите программу вычисления произведения cos5°xcos]00xcosl5°x…xcos850.

215. Напишите программу вычисления суммы:

216. Напишите программу, рисующую цепочку соприкасающихся окружностей с заданными в операторе data радиусами (рис. 1.63).


Рис. 1.63. Цепочка соприкасающихся окружностей

217. Создайте программу вычисления среднего роста десяти человек, данные о которых занесены в оператор data.

218. Напишите программу вычисления среднего балла при поступлении в институт по результатам четырех экзаменов, которые вводятся с клавиатуры.

219. С помощью Бейсика вычислите среднее геометрическое трех произвольных чисел. Среднее геометрическое есть корень степени N из произведения N чисел.

Нахождение суммы последовательности целых чисел

Когда в вопросе предлагается сложить большое количество целых чисел, может показаться, что поиск ответа может занять некоторое время.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам Но GMAT — это умные ярлыки. Вот быстрый метод, который сделает вас счастливыми, если вы будете получать такие вопросы в день экзамена.

Рассмотрим следующий вопрос от наставника Economist GMAT:

Для каждого положительного целого числа n n-й член последовательности представляет собой сумму трех последовательных целых чисел, начинающихся с n.Какова сумма членов с 1 по 99 этой серии?

Правила быстрого нахождения суммы этой последовательности целых чисел

Правило № 1: Сумма последовательности целых чисел — это среднее значение последовательности целых чисел, умноженное на количество членов.

Если это правило звучит знакомо, это потому, что это просто другая версия формулы для нахождения среднего:

  • Среднее = Сумма терминов / Количество терминов

Теперь, как мы можем определить среднее значение последовательность целых чисел?

Правило № 2: Среднее значение последовательности целых чисел — это среднее значение первого и последнего членов.

Применение правил для нахождения суммы последовательности

Как мы применим эти полезные правила к этому вопросу?

Сначала вычислите среднее значение первого и последнего членов.

  • Первый член представляет собой сумму 1, 2 и 3 = 6
  • Последний член представляет собой сумму 99, 100 и 101 = 300
  • Среднее значение первого и последнего членов = (6 + 300) / 2 = 306/2 = 153

Во-вторых, умножьте среднее значение на количество членов.

  • Есть 99 терминов
  • Следовательно, ответ на наш вопрос: 153 x 99

Обратите внимание, что быстрый способ вычислить это без калькулятора — это умножить 153 x 100 и вычесть 153.

  • 153 x 100 = 15 300
  • 15 300 — 153 = 15 147

И это наш окончательный ответ!

Вы можете увидеть, как применение простых правил значительно упрощает вопросы, которые кажутся сложными.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам Ваша задача собрать как можно больше таких правил.

Это был образец подробных инструкций, которые Economist GMAT Tutor предлагает по решению задач в разделе GMAT Quant. Чтобы получить полные и интерактивные уроки, практические тесты и поддержку онлайн-преподавателей, подпишитесь на один из самых популярных планов подготовки к GMAT от Economist GMAT Tutor.Пробные версии без обязательств доступны в течение семи дней.

Как найти количество целых чисел между двумя другими целыми числами

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т.Чему равна сумма чисел от 0 до 100 включительно: Поиск по вопросам д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Написать на Python Написать программу; A. Отображает S …

Запись на Python

Напишите программу;

а. отображает сумму всех четных чисел от 2 до 100 (включительно).

г. отображает сумму всех квадратов от 1 до 100 (включительно).

г. отображает степени 2 от 1 до 256.

г. отображает сумму всех нечетных чисел от a до b (включительно), где a и b — входные данные.

e. отображает сумму всех нечетных цифр ввода. (Например, если ввод 32677, сумма будет 3 + 7 + 7 = 17.)

Вы должны выполнять каждый шаг с помощью цикла.

пробный прогон:

Все четные числа от 2 до 100 включительно:
2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60 62 64 66 68 70 72 74 76 78 80 82 84 86 88 90 92 94 96 98100
Сумма четных чисел от 2 до 100 составляет 2550

Все квадраты с цифрами от 2 до 30 включительно:
1 4 9 16 25 36 49 64 81 100 121 144 169 196225 256 289 324 361 400 441 484 529 576 625 676 729 784 841 900
Сумма всех квадратов от 1 до 30 составляет 9455

Все степени двойки от 2 ** 0 до 2 ** 8:
2 ** 0 равно 1
2 ** 1 равно 2
2 ** 2 равно 4
2 ** 3 равно 8
2 ** 4 равно 16
2 ** 5 — 32
2 ** 6 — 64
2 ** 7 — 128
2 ** 8 — 256

Вычислить сумму всех нечетных целых чисел между двумя целыми числами:
Введите целое число: 2
Введите другое целое число: 15
3 5 7 9 11 13 15
Сумма нечетных чисел от 2 до 15 составляет 63

Вычислить сумму нечетных цифр целого числа
Введите целое число: 675432
Общее количество нечетных цифр в 675432 равно 15

Рубрика

задание 4 Рубрика

задание 4 Рубрика

Критерии Рейтинги Баллы Этот критерий связан с обучением. Результат Все строки имеют правильный отступ 1.0 баллов Этот критерий связаны с Результатом обучения Комментарии в верхней части программы: Имя / дата / чем занимается ваша программа. 2,0 балла Это критерий связан с результатом обучения. комментарий в конце вашего кода, у вас должен быть хотя бы один прогон. 2,0 балла Этот критерий связан с результатом обучения. хорошо организован. Пример: value1 = value2 + 3 # плохой стиль значение1 = значение2 + 3 # хороший стиль 2,0 балла Этот критерий связан к результату обучения Имена ваших переменных имеют значение 2.0 баллов Этот критерий связан с комментарием к результатам обучения перед любым петля. 2,0 балла Этот критерий связан с результатом обучения программа работает с правильным выводом. Все выходы должны быть с округлением до одного десятичного знака. 12.0 баллов Этот критерий связан с комментарий к результатам обучения перед любым блоком if. 2,0 балла Это критерий связан с результатом обучения; петля используется для достижения каждый шаг. 5,0 баллов Всего баллов: 30,0

Упражнения на C ++: Найдите число и сумму всех целых чисел от 100 до 200, которые делятся на 9

C ++ For Loop: Упражнение 28 с решением

Напишите программу на C ++, чтобы найти число и сумму всех целых чисел от 100 до 200, которые делятся на 9.

Изображение:

Пример раствора : —

Код C ++: 

  #include 
используя пространство имен std;

int main ()
{
    int i, сумма = 0;
    cout << "\ n \ n Найдите число и сумму всех целых чисел от 100 до 200, делящихся на 9: \ n";
    cout << "---------------------------------------------- ---------------------------------- \ n ";
    cout << "Числа от 100 до 200, кратные 9:" << endl;
    для (я = 101; я <200; я ++)
    {
        если (я% 9 == 0)
        {
            cout << "" << я;
            сумма + = я;
        }
    }
    cout << "\ n Сумма:" << sum << endl;
}

Пример вывода:

 Найдите число и сумму всех целых чисел от 100 до 200, делящихся на 9:
-------------------------------------------------- ------------------------------
 Числа от 100 до 200, кратные 9:
 108 117 126 135 144 153 162 171 180 189 198
 Сумма: 1683

Схема:

Редактор кода C ++:

Публикуйте свой код и комментарии через Disqus.

Предыдущая: Напишите программу на C ++ для отображения первых n членов ряда Фибоначчи.
Далее: Напишите программу на C ++, чтобы найти НОК любых двух чисел с помощью HCF.

Программа Python для вычисления суммы четных чисел

Напишите программу на Python для вычисления суммы четных чисел от 1 до N, используя цикл while и For Loop с примером.

Программа Python для вычисления суммы четных чисел от 1 до N с использованием цикла For

Эта программа Python позволяет пользователю вводить максимальное предельное значение.Затем Python рассчитает сумму четных чисел от 1 до введенного пользователем значения.

В этом примере мы используем Python For Loop, чтобы сохранить число от 1 до максимального значения.

СОВЕТ: Я предлагаю вам обратиться к статье Python «Четные числа от 1 до N», чтобы понять логику печати четных чисел в Python.

 # Программа на Python для вычисления суммы четных чисел от 1 до N
 
maximum = int (input ("Пожалуйста, введите максимальное значение:"))
всего = 0

для числа в диапазоне (1, максимум + 1):
    если (число% 2 == 0):
        печать ("{0}".формат (число))
        итого = итого + число

print ("Сумма четных чисел от 1 до {0} = {1}". format (number, total))

Программа Python для вычисления суммы четных чисел от 1 до N без оператора If

Эта программа Python для вычисления суммы четных чисел такая же, как и выше. Но мы изменили цикл Python For Loop, чтобы удалить блок If.

 # Программа на Python для вычисления суммы четных чисел от 1 до N
 
maximum = int (input ("Пожалуйста, введите максимальное значение:"))
всего = 0

для числа в диапазоне (2, максимум + 1, 2):
    печать ("{0}".формат (число))
    итого = итого + число

print ("Сумма четных чисел от 1 до {0} = {1}". format (number, total))

Программа Python для поиска суммы четных чисел с использованием цикла while

В этом примере Python с суммой четных чисел мы заменили цикл For на цикл While Loop.

 # Программа на Python для вычисления суммы четных чисел от 1 до N
 
maximum = int (input ("Пожалуйста, введите максимальное значение:"))
всего = 0
число = 1
 
а число <= максимум:
    если (число% 2 == 0):
        печать ("{0}".формат (число))
        итого = итого + число
    число = число + 1

print («Сумма четных чисел от 1 до N = {0}». формат (всего))

Программа Python для поиска суммы четных чисел от 1 до 100

Эта программа Python позволяет пользователям вводить минимальное и максимальное значение. Затем Python вычисляет сумму четных чисел от минимального до максимального значения.

 # Программа на Python для вычисления суммы четных чисел от 1 до 100

минимум = int (input («Пожалуйста, введите минимальное значение:»))
maximum = int (input ("Пожалуйста, введите максимальное значение:"))
всего = 0

для числа в диапазоне (минимум, максимум + 1):
    если (число% 2 == 0):
        печать ("{0}".формат (число))
        итого = итого + число

print ("Сумма четных чисел от {0} до {1} = {2}". format (минимум, число, всего))
Учебное пособие по Python

: циклы для циклов

Предыдущая глава: Циклы пока
Следующая глава: Форматированный вывод

Для петель

Введение

Как и цикл while, цикл for является оператором языка программирования, то есть оператором итерации, что позволяет повторять блок кода определенное количество раз.

Вряд ли есть языки программирования без циклов for, но цикл for существует во многих разные вкусы, т.е.е. синтаксис и семантика отличаются от одного языка программирования к другому.

Различные виды петель for:

  • Цикл for с управлением по счету (три выражения для цикла)
    Это, безусловно, наиболее распространенный тип. Это утверждение использовалось К. Заголовок цикла for этого типа состоит из трехпараметрического управляющего выражения цикла. Как правило, это форма:
    для (A; Z; I)
    A - часть инициализации, Z определяет выражение завершения, а I - выражение счета, где переменная цикла увеличивается или уменьшается.Примером такого цикла является цикл for языка программирования C:
    для (i = 0; i
    Такой цикл for не реализован в Python!
  • Числовые диапазоны
    Этот вид цикла for является упрощением предыдущего вида. Это цикл подсчета или перечисления. Начиная с начального значения и считая до конечного значения, например для i = от 1 до 100
    Python также не использует это.
  • Векторизация для петель
    Они ведут себя так, как будто все итерации выполняются параллельно.Это означает, например, что все выражения в правой части операторов присваивания оцениваются перед присваиваниями.
  • Итератор для цикла
    Наконец, мы подошли к тому, что используется в Python. Этот вид цикла for выполняет итерацию по перечислению набора пунктов. Обычно для него характерно использование неявного или явного итератор. На каждом шаге итерации переменной цикла присваивается значение в последовательности или другом сбор информации. Этот вид цикла for известен в большинстве оболочек Unix и Linux, и именно он реализован на Python.

Синтаксис цикла For

Как мы упоминали ранее, цикл for в Python представляет собой итератор, основанный на цикле for. Он проходит через элементы списков, кортежи, строки, ключи словарей и другие итерации. Цикл for Python начинается с ключевого слова "for", за которым следует произвольное имя переменной, который будет содержать значения следующего объекта последовательности, который проходит через него. Общий синтаксис выглядит так: 

для <переменная> в <последовательности>:
<заявления>
еще:
<заявления>
Элементы объекта последовательности назначаются один за другим переменной цикла; чтобы быть точным, переменная указывает на элементы.Для каждого элемента выполняется тело цикла.

Пример простого цикла for в Python:

>>> languages ​​= ["C", "C ++", "Perl", "Python"]
>>> для x в языках:
... печать (x)
...
C
C ++
Perl
Python
>>>

Блок else особенный; хотя программисты Perl знакомы с этим, это неизвестная концепция программистам на C и C ++. Семантически он работает точно так же, как необязательный else цикла while. Он будет выполнен только в том случае, если цикл не был «прерван» оператором break.Таким образом, он будет выполнен только после того, как все элементы последовательности в заголовке будут использовал.

Если оператор break должен быть выполнен в потоке программы цикла for, цикл будет будет завершен, и выполнение программы продолжится с первого оператора, следующего за циклом for, если вообще есть. Обычно операторы break заключаются в условные операторы, например 

edibles = ["ветчина", "спам", "яйца", "орехи"]
для еды в пищу:
    если еда == "спам":
        print («Пожалуйста, хватит спама!»)
        перерыв
    print ("Отлично, вкусно" + еда)
еще:
    print («Я так рад: спама нет!»)
print («Наконец-то я закончил набивать себе голову»)
Если мы вызовем этот скрипт, мы получим следующий результат:
$ python для.ру
Отличная, вкусная ветчина
Пожалуйста, больше никакого спама!
Наконец-то закончил набивать себе
$
Удалив «спам» из нашего списка съедобных, мы получим следующий результат:
$ python for.py
Отличная, вкусная ветчина
Отличные, вкусные яйца
Отличные, вкусные орехи
Я так рада: никакого спама!
Наконец-то закончил набивать себе
$
Может быть, наше отвращение к спаму не настолько велико, чтобы мы перестали есть другую еду. Теперь это вызывает в игру оператор continue. В следующих небольшой скрипт, мы используем оператор continue, чтобы продолжить наш список съедобных, когда у нас есть обнаружил спам.Так что continue мешает нам есть спам!
edibles = ["ветчина", "спам", "яйца", "орехи"]
для еды в пищу:
    если еда == "спам":
        print («Пожалуйста, хватит спама!»)
        Продолжать
    print ("Отлично, вкусно" + еда)
    # здесь может быть код для наслаждения нашей едой :-)
еще:
    print («Я так рад: спама нет!»)
print («Наконец-то я закончил набивать себе голову»)
Результат выглядит следующим образом:
$ python for.py
Отличная, вкусная ветчина
Пожалуйста, больше никакого спама!
Отличные, вкусные яйца
Отличные, вкусные орехи
Я так рада: никакого спама!
Наконец-то закончил набивать себе
$

Функция range ()

Встроенная функция range () - это правильная функция для итерации по последовательность чисел.Он генерирует итератор арифметических прогрессий:
Пример:

>>> диапазон (10)
диапазон (0, 10)
>>> список (диапазон (10))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>>
range (n) генерирует итератор для продвижения целых чисел, начиная с 0 и заканчивая (n -1). Чтобы составить список с этими числами, мы должны преобразовать range () с помощью list (), как мы это делали в предыдущем примере.
range () также можно вызвать с двумя аргументами:
диапазон (начало, конец)
Вышеупомянутый вызов создает итератор списка чисел, начинающихся с begin (включительно) и оканчивается на единицу меньше числа "конец".
Пример:
>>> диапазон (4,10)
диапазон (4, 10)
>>> список (диапазон (4,10))
[4, 5, 6, 7, 8, 9]
>>>

До сих пор приращение range () составляло 1. Мы можем указать другое приращение. с третьим аргументом. Приращение называется «шагом». Может быть как отрицательным и положительный, но не ноль:
диапазон (начало, конец, шаг)
Пример с шагом:
>>> список (диапазон (4,50,5))
[4, 9, 14, 19, 24, 29, 34, 39, 44, 49]
>>>
Это также можно сделать в обратном направлении:
>>> список (диапазон (42, -12, -7))
[42, 35, 28, 21, 14, 7, 0, -7]
>>>
Функция range () особенно полезна в сочетании с циклом for, так как мы можем видеть в следующем примере.Функция range () предоставляет числа от 1 до 100 для цикла for, чтобы вычислить сумму этих чисел:
n = 100

сумма = 0
для счетчика в диапазоне (1, n + 1):
    сумма = сумма + счетчик

print ("Сумма от 1 до% d:% d"% (n, sum))

Вычисление чисел Пифагора

Обычно предполагается, что теорема Пифагора была открыта Пифагором, т.е. почему у него такое название. Но есть споры о том, могла ли теорема Пифагора иметь были обнаружены ранее или другими независимо.Для пифагорейцев - мистическое движение, основанные на математике, религии и философии, - целые числа, удовлетворяющие теореме, были специальные числа, которые были для них священными.

В наши дни числа Пифагора больше не являются мистическими. Хотя некоторым ученикам в школе или другие люди, которые не в хороших отношениях с математикой, они все еще могут казаться таковыми.

Итак, определение очень простое:
Три целых числа, удовлетворяющие а 2 + б 2 = в 2 называются числами Пифагора.

Следующая программа вычисляет все числа Пифагора, меньшие максимальное количество.
Примечание: Мы должны импортировать математический модуль, чтобы иметь возможность вычислять квадратный корень из числа.

из математического импорта sqrt
n = int (input ("Максимальное число?"))
для диапазона (1, n + 1):
    для b в диапазоне (a, n):
        c_square = a ** 2 + b ** 2
        c = int (sqrt (c_square))
        если ((c_square - c ** 2) == 0):
            печать (a, b, c)

Перебор списков с помощью range ()

Если вам нужно получить доступ к индексам списка, не будет хорошей идеей используйте цикл for для перебора списков.Мы можем получить доступ ко всем элементам, но индекс элемента недоступен. Но есть способ получить доступ как к индексу элемент и сам элемент. Решение состоит в использовании range () в комбинации с функцией длины len ():
фибоначчи = [0,1,1,2,3,5,8,13,21]
для i в диапазоне (len (fibonacci)):
    print (я, фибоначчи [я])
Распечатать()
Результат выглядит так:
0 0
1 1
2 1
3 2
4 3
5 5
6 8
7 13
8 21
Примечание: если вы примените len () к списку или кортежу, вы получите количество элементов эта последовательность.

Перечислить итерацию с побочными эффектами

Если вы перебираете список в цикле, лучше избегать изменения списка в теле цикла. Чтобы дать вам пример того, что может случиться, взгляните на следующий пример:
цвета = ["красный"]
для i в цветах:
    если я == "красный":
        цвета + = ["черный"]
    если я == "черный":
        цвета + = ["белый"]
печать (цвета)
Что напечатает «печать (цвета)»?
['красный', 'черный', 'белый']
Чтобы избежать этих побочных эффектов, лучше всего работать с копией с помощью оператора среза, как и можно увидеть в следующем примере:
цвета = ["красный"]
для i в цветах [:]:
    если я == "красный":
        цвета + = ["черный"]
    если я == "черный":
        цвета + = ["белый"]
печать (цвета)
Теперь результат выглядит так:
['красный', 'черный']
Мы все еще могли сделать что-то, чего не должны были делать.Мы изменили список "цветов", но наше изменение больше не повлияло на цикл. Элементы, которые нужно было зациклить, оставались то же самое во время итераций. Предыдущая глава: Циклы while
Следующая глава: Форматированный вывод

Цикл while - изучение Python 3


при повторении цикла последовательность действий много раз, пока какое-то условие не оценивается как Ложь . Условие задается перед телом цикла и проверяется перед каждым выполнением тела цикла.Обычно цикл и используется, когда это невозможно. чтобы заранее определить точное количество итераций цикла.

Синтаксис цикла while в простейшем случае выглядит так:

 при каком-то условии:
    блок заявлений

Python сначала проверяет условие. Если ложно, то цикл прерывается и управление передается в следующий оператор после тела цикла while . Если условие истинно, то выполняется тело цикла, а затем условие проверяется снова.Это продолжается, пока условие истинно. Как только условие становится ложным, цикл завершается и управление передается следующему оператору после цикла.

Например, следующий фрагмент программы распечатывает квадраты всех целых чисел от 1 до 10. Здесь можно заменить цикл while на для ... в диапазоне (...) петля:

 1
4
9
16
25
36
49
64
81 год
100
 
 я = 1
пока я <= 10:
    печать (я ** 2)
    я + = 1

В этом примере переменная i внутри цикла повторяется от 1 до 10.Такая переменная, значение которой изменяется с каждой новой итерацией цикла. называется счетчиком. Обратите внимание, что после выполнения этого фрагмента значение переменной i определено и равно 11 , потому что, когда i == 11 условие i <= 10 является ложным в первый раз.

Вот еще один пример использования цикла и для определения количества цифр целого числа n :

 5678
 
 п = целое число (вход ())
длина = 0
пока n> 0:
    n // = 10 # это эквивалентно n = n // 10
    длина + = 1
печать (длина) # 4

На каждой итерации отрезаем последнюю цифру числа с использованием целочисленного деления на 10 ( n // = 10 ).В переменной длина посчитаем, сколько раз мы это сделали.

В Python есть другой, более простой способ решить эту проблему: длина = len (str (i)) .

Можно написать оператор else: после тела цикла, который выполняется один раз после окончания цикла:

 Нет 
 я = 1
пока я <= 10:
    печать (я)
    я + = 1
еще:
    print ('Цикл закончился, я =', я)

На первый взгляд это утверждение кажется бессмысленным, потому что утверждение else: тело можно просто поставить после конца петли.Оператор "else" после цикла имеет смысл только при использовании в сочетании с инструкцией перерыв . Если во время выполнения цикла интерпретатор Python обнаруживает break , он немедленно останавливает выполнение цикла и выходит из него. В этом случае ветвь else: не выполняется. Итак, break используется для прерывания выполнения цикла во время середина любой итерации.

Вот пример, похожий на Black Jack: программа, которая считывает числа и суммирует их. пока общая сумма не станет больше или равна 21.Входная последовательность заканчивается на 0 чтобы программа могла остановиться, даже если общая сумма всех чисел меньше 21.

Посмотрим, как он себя ведет на разных входах.

Версия 1. Цикл завершается нормально после проверки условия, поэтому "else" филиал выполнен.

 2
4
7
0
 
 total_sum = 0
а = int (вход ())
а! = 0:
    total_sum + = a
    если total_sum> = 21:
        print ('Общая сумма', total_sum)
        перерыв
    а = int (вход ())
еще:
    print ('Общая сумма меньше 21 и равна', total_sum, '.')

Версия 2. Цикл прерывается break , поэтому "else" ветка пропущена.

 9
9
5
4
0
 
 total_sum = 0
а = int (вход ())
а! = 0:
    total_sum + = a
    если total_sum> = 21:
        print ('Общая сумма', total_sum)
        перерыв
    а = int (вход ())
еще:
    print ('Общая сумма меньше 21 и равна', total_sum, '.')

Ветвь «Else» также может использоваться с циклом «for». Давайте посмотрим на пример, когда программа читает 5 целых чисел но останавливается сразу, когда встречается первое отрицательное целое число.

Версия 1. Выход из цикла происходит нормально, поэтому выполняется ветвь "else".

 3
6
2
4
5
 
 для i в диапазоне (5):
    а = int (вход ())
    если a <0:
        print ('Встретил отрицательное число', а)
        перерыв
еще:
    print ('Никаких отрицательных чисел не встречалось')

Версия 2. Цикл прерван, поэтому ветвь «else» не выполняется.

 3
6
-2
4
5
 
 для i в диапазоне (5):
    а = int (вход ())
    если a <0:
        print ('Встретил отрицательное число', а)
        перерыв
еще:
    print ('Никаких отрицательных чисел не встречалось')

Другая инструкция, используемая для управления выполнением цикла: продолжить .Если интерпретатор Python встречает , продолжайте где-то в середине итерации цикла, он пропускает все оставшиеся инструкции и переходит к следующей итерации.

 Нет 
 для числа в диапазоне (2, 10):
    если число% 2 == 0:
        print ("Найдено четное число", num)
        Продолжать
    print ("Нашел номер", num)

Если break и continue помещаются внутри нескольких вложенных петли, они влияют только на выполнение самого внутреннего.Давайте посмотрим на довольно глупый пример для демонстрации:

 Нет 
 для i в диапазоне (3):
    для j в диапазоне (5):
        если j> i:
            # ломает только for в строке 2
            перерыв
        печать (я, j)

Инструкции break и continue обескуражены, если вы можете реализовать свою идею, не используя их. Вот типичный пример неправильного использования разрыва : этот код подсчитывает количество цифр целого числа.

 567
 
 п = целое число (вход ())
длина = 0
в то время как True:
    длина + = 1
    п // = 10
    если n == 0:
        перерыв
print ('Длина', длина)

Переписать этот цикл с осмысленным условием цикла чище и легче для чтения:

 567
 
 п = целое число (вход ())
длина = 0
а n! = 0:
    длина + = 1
    п // = 10
print ('Длина', длина)

В Python один оператор присваивания может изменять значение нескольких переменных.Посмотрим:

Эффект, продемонстрированный выше, код можно записать как:

Разница между двумя версиями заключается в том, что множественное присвоение изменяет значения двух переменных одновременно.

Множественное присвоение полезно, когда вам нужно обменять значения двух переменных. В старых языках программирования без поддержки множественного присваивания это можно сделать с помощью вспомогательной переменной:

 Нет 
 а = 1
b = 2
tmp = a
а = б
b = tmp
печать (а, б)
# 2 1

В Python тот же своп можно записать одной строкой:

 Нет 
 а = 1
b = 2
а, б = б, а
печать (а, б)
# 2 1

В левой части знака "=" должен быть список имен переменных, разделенных запятыми.

You May Also Like

Leave a Reply