Ассоциативная таблица умножения: Ассоциативная таблица умножения – купить на Ярмарке Мастеров – CAZOJRU

Выучить таблицу умножения — ТОП 8 методов. ⋆ Таблица умножения

u

выучить таблицу умножения и не угробить психику ребенка

В основном учителя просят выучить Таблицу умножения на летних или зимних каникулах.

Потому что: На каникулах ребенок не загружен учебой. Есть свободное время. Он может выучить Таблицу умножения в своем темпе. Чтобы потом не отставать и избежать плохих оценок.

 

Поэтому вся ответственность ложится на плечи родителей. Которым приходится выслушивать:

Думаю, многие родители вспомнят себя в этот период жизни:)

1 — Зазубривание

 

Начну с самого привычного:)

+

Однозначно, к плюсам можно отнести известность методики. Так учили мы и наши бабушки. От постоянного бубнения включается аудиальная память.

—

Но, к сожалению, большинство детей относятся к визуалам и кинестетам, поэтому такой способ выучить таблицу умножения становится скучным, продолжительным и неприятным. Также, отсутствует осознанное запоминание, поэтому ребенок часто путается и не уверен в правильном ответе.

 

2 — Высчитывание, сложение и вычитание

 

+

Этот способ для предприимчивых отличников, которые хорошо понимают принципы умножения и довольно шустро умеют складывать в уме.

—

Но, если ваш ребенок еще не достаточно овладел скоростным счетом, то он будет долго думать над ответом. И, конечно, теряется весь смысл изобретения таблицы Пифагора — давать мгновенный результат вычисления.

Если постоянно высчитывать, то значение произведения не запоминается. Поэтому шансов овладеть знанием Таблицы Умножения тоже немного.

 

3 — Многократное списывание. карточки с ответами на видных местах

 

+

Запоминание, которое включает в себя воздействие только на зрительную память. Хорошо подходит визуалам.

— 

Поэтому запоминание может быть очень продолжительным.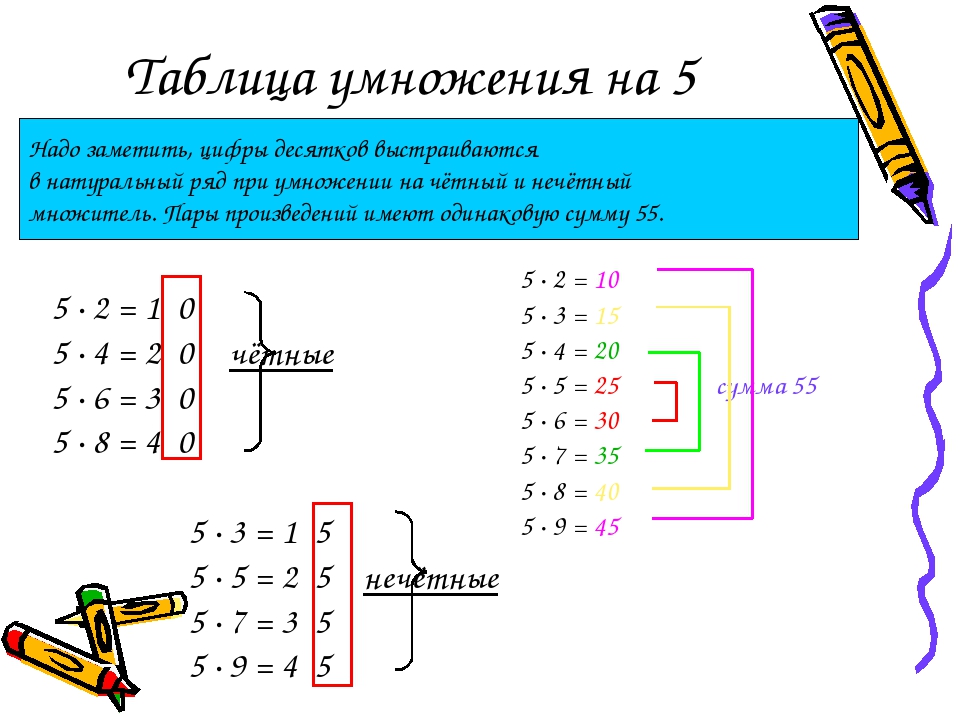 Опасно тем, что концентрация внимания на запоминаемом объекте значительно снижается: рука механически выполняет одни и те же действия, а глаза смотрят на цифры, не осознавая их значение.

Если сказать по-простому — «замыливается глаз».

 

4 — умножение на пальцах

 

+

Задорно и популярно сейчас на YouTube. Конечно, метод очень доступный, так как пальцы всегда «под рукой». Идеально подойдет кинестетикам, чтобы выучить таблицу умножения.

—

К удачному способу запоминания его тоже трудно отнести. С помощью пальцев легко получить ответ только на 9. Остальные комбинации нужно высчитывать с помощью сложения и того же умножения. Большой недостаток, что пальцы не помогут в делении:)

 

5 — Поделки своими руками: книжки, оригами, картинки

 

+

Один из самых приятных способов выучить таблицу умножения. Он предполагает совместную и эмоциональную работу вместе с мамой.

Прекрасно подойдёт кинестетикам и визуалам. Включает в себя разъяснение и понимание принципов умножения.

—

Но может быть непредсказуем по длительности обучения. Также, необходимо участь затраты времени для изготовления материалов.

 

6 — стихи, песни, реп

 

+

Рифма помогает легче запомнить произведение. Обучение может стать интересным, если ребенок аудиал и быстро схватывает на слух.

—

Но, не подойдет детям, у которых трудности с запоминанием стихотворений. Возникнут сложности, когда нужно будет переходить на деление.

 

7 — Карточки с примерами, раскраски, приложения, книги-тренажеры, интерактивные доски

 

+

У ребенка включается некий азарт. Активно работают все типы восприятия. За счет частых и обдуманных повторений происходит осознанное долгосрочное запоминание.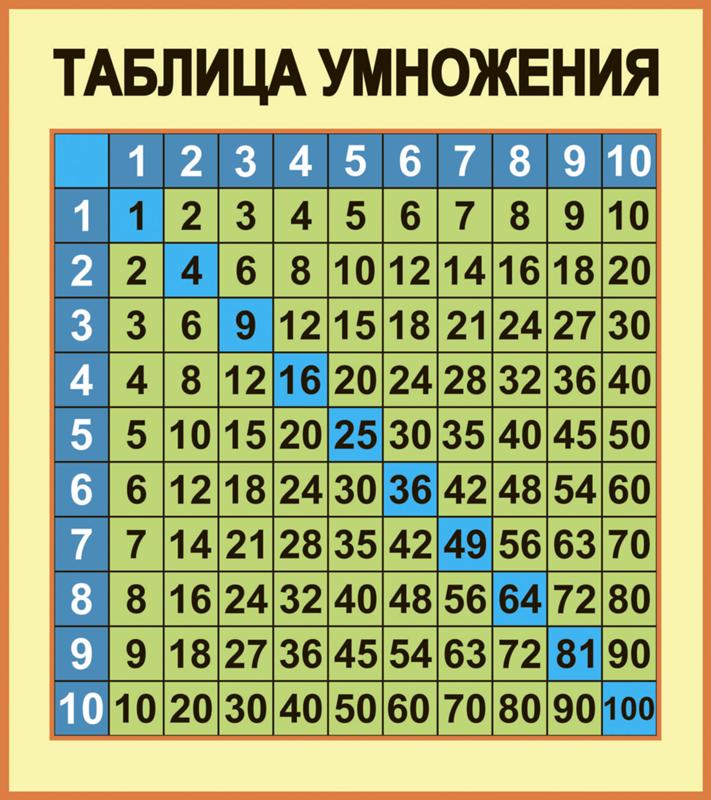 Есть возможность акцентировать больше внимание на плохо запомнившихся комбинациях.

Лучше всего подходят для повторения, когда ребенок уже выучил Таблицу умножения и закрепляет результат.

—

Если использовать эти методики для обучения, то частые ошибки могут расстроить ребенка и вызвать нежелание работать дальше.

 

Я постаралась максимально глубоко раскрыть плюсы и минусы каждого способа.

Конечно же, выбор лучше делать исходя из характера и усидчивости ребенка. Если изначально ребенок испытывает трудности с запоминанием информации, то лучше обратить внимание на последний способ. Так как через образность выучить Таблицу умножения ему будет быстрее и проще всего.

 

Помню, с каким трудом сама зубрила таблицу во 2-м классе. Ну не запоминается и всё. Аж до слез! И знаю, что трудности с запоминания возникают у многих. Это негативно сказывается на самооценке ребенка, совершенно отбивает желание учиться, и лишает его возможности наслаждаться учебным процессом.

 

Учитесь с удовольствием!   Светлана Соловей. Сертифицированный тренер по эйдетике и мнемотехнике, скорочтению. Преподаватель Гимнастики для мозга «Brain-Gym» . Автор курсов «Таблица Умножения за 3 часа», «Хочу учиться!», «Внимание! Мозг», «Мозг UP», «Скорочтение 5/30» Приглашенный эксперт на радио и телевидение, спикер на всеукраинских фестивалях.

Как легко запомнить таблицу умножения

На первый взгляд таблица умножения кажется громоздкой. 100 элементов! Ребенок, наверное, даже не ожидает, что такое придется учить. Но есть несколько способов, как можно выучить данную таблицу быстрее, чем зубрежка. Некоторые из них сложные и мало результативные, другие же наоборот очень эффективные.

Таблица умножения

И одним из таких эффективных методов я поделюсь. Он основан на последовательности изучения отдельных таблиц для отдельных чисел и знания их некоторых закономерностей.

Как быстро запомнить таблицу умножения

Половину таблицы умножения даже нет смысла учить.

Умножение на 1, 2, 10. Это очевидно, как умножать цифры на 1 и на 10. А умножение на 2 это очень простое сложение числа с самим собой.

2 x 2 = 2 + 2 = 4
6 x 2 = 6 + 6 = 12
9 x 2 = 9 + 9 = 18

Умножение на 1 и 10

Соответственно к тому времени, как учить таблицу умножения ребенок должен знать, что такое сложение чисел. Теперь когда мы разобрались с умножением на 1, 2, 10 остается таблица всего лишь из 49 элементов.

Оставшаяся таблица

Умножение на 3, 4. Основные сложности, замеченные мной, при запоминании таблицы умножения —  это умножения на 3 и на 4. Когда вы изучите это, останется совсем немного.

Я предлагаю выучить последовательность (результаты произведения чисел при умножении на 3) : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 так, чтобы научиться достаточно быстро называть данную последовательность.

Далее предлагаю последовательно задавать вопрос
«3 умножить на 1»  — 3!
«3 умножить на 2»  — 6!
«3 умножить на 3» — 9!
«3 умножить на 4» — 12!
…. .
«3 умножить на 10» — 30!

Таким образом, мы сопоставляем ту последовательность (результаты умножения на 3), которую выучили ранее с множителями цифры 3. Далее предлагаю делать это в произвольном порядке:

«3 умножить на 3»  — 9!
«3 умножить на 1» — 3!
«3 умножить на 7» — 21!

До тех пор, пока не усвоится умножение на 3.

То же самое мы делаем и с умножением на 4. Учим последовательность 4, 8, 12, 16, 20, 24, 28, 32, 36, 40.

Последовательно проходим
«4 умножить на 1» — 4!
«4 умножить на 2» — 8!
«4 умножить на 3» — 12!
«4 умножить на 4» — 16!
…..
«4 умножить на 10» — 40!

И далее в случайном порядке
«4 умножить на 7» — 28!
«4 умножить на 3» — 12!
«4 умножить на 6» — 24!

Умножение на 5. Умножение на 5 учится легко, т.к. произведении любого числа на 5 заканчивается либо на 0, либо на 5.

Умножение на 9. Для умножения на 9 есть интересный прием

9 x 1  = 09
9 x 2  = 18
9 x 3  = 27
9 x 4  = 36
9 x 5  = 45
9 x 6  = 54
9 x 7  = 63
9 x 8  = 72
9 x 9  = 81
9 x 10  = 90

Во-первых, сумма цифр произведения дает нам 9.

9 x 2  = 18 (1 + 8 = 9)
9 x 3  = 27 (2 + 7 = 9)
9 x 4  = 36 (3 + 6 = 9)
9 x 5  = 45 (4 + 5 = 9)

Во-вторых, число множителя 9 на 1 больше, чем первая цифра в результате произведения

9 x 2  = 18 (9 умножить на 2 результат начинается с единицы)
9 x 3  = 27 (9 умножить на 3 результат начинается с двойки)
9 x 4  = 36 (9 умножить на 4 результат начинается с тройки)
9 x 5  = 45 (9 умножить на 5 результат начинается с четверки)

Используя 2 этих факта, можно значительно упростить задачу запоминания умножения на 9.

Теперь, когда мы знаем таблицу умножения на 1, 2, 3, 4, 5, 9, 10. Остается небольшой кусочек:

Легко запомнить

Многие находят достаточно легким выучить умножение числа на само себя (квадрат числа)

6 x 6  = 36
7 x 7  = 49
8 x 8  = 64

И тогда остается 3 «сложных» факта:

7 x 6 = 6 x 7 = 42
8 x 6 = 6 x 8 = 48
8 x 7 = 7 x 8 = 56

Их нужно просто выучить.

В итоге разложив всё на поэтапные шаги, понимаем, что запомнить таблицу умножения не так уж и сложно.

Для повторения таблицы умножения советую использовать карточки, но именно для повторения!

Просто пройдите последовательно по всем шагам  и повторяйте запомненную таблицу по карточкам и быстрые результаты не заставят себя ждать!

Понравилась статья? Поделитесь с друзьями:

Вконтакте

Facebook

Twitter

Google

Telegram

абстрактная алгебра. Есть ли простой способ увидеть ассоциативность или неассоциативность из таблицы операций?

спросил 10 лет, 3 месяца назад

Изменено 2 года назад

Просмотрено 19 тысяч раз

$\begingroup$

Большинство свойств одной бинарной операции можно легко прочитать из таблицы операций. Например, учитывая $$\begin{массив}{c|ccccc} \cdot & a & b & c & d & e\\\hline а, д, г, б, а, в\\ б & г & в & д & б & а\\ в и б и д и а и в и г\\ д & а & ​​б & в & д & д \\ е и с и а и г и е и б \end{массив}$$ легко проверить, что она замкнута (в таблице нет элементов, которые не встречаются в качестве индекса строки или столбца), коммутативна (таблица симметрична), имеет нейтральный элемент (строка и столбец $d$ равны копии строки/столбца индекса) и имеет обратный элемент для каждого элемента (в каждой строке и столбце есть $d$).

Другими словами, почти все важные свойства видны сразу. Не хватает только ассоциативности.

Поэтому мой вопрос: есть ли простой способ увидеть непосредственно из таблицы операций (т. е. без явного выполнения всех вычислений), является ли операция ассоциативной?

• абстрактная алгебра
• конечные группы
• ассоциативность
• магма
• таблица Кэли

$\endgroup$

0

$\begingroup$

Вы видели тест Лайта на ассоциативность? Согласно Википедии, «прямая проверка ассоциативности бинарной операции, заданной таблицей Кэли, громоздка и утомительна. Тест ассоциативности Лайта значительно упрощает задачу». 93$ тождеств вида $(a\ast b)\ast c = a\ast (b\ast c)$. Это связано с тем, что операция может быть полностью ассоциативной

, за исключением для одной плохой тройки $\langle a,b,c\rangle$.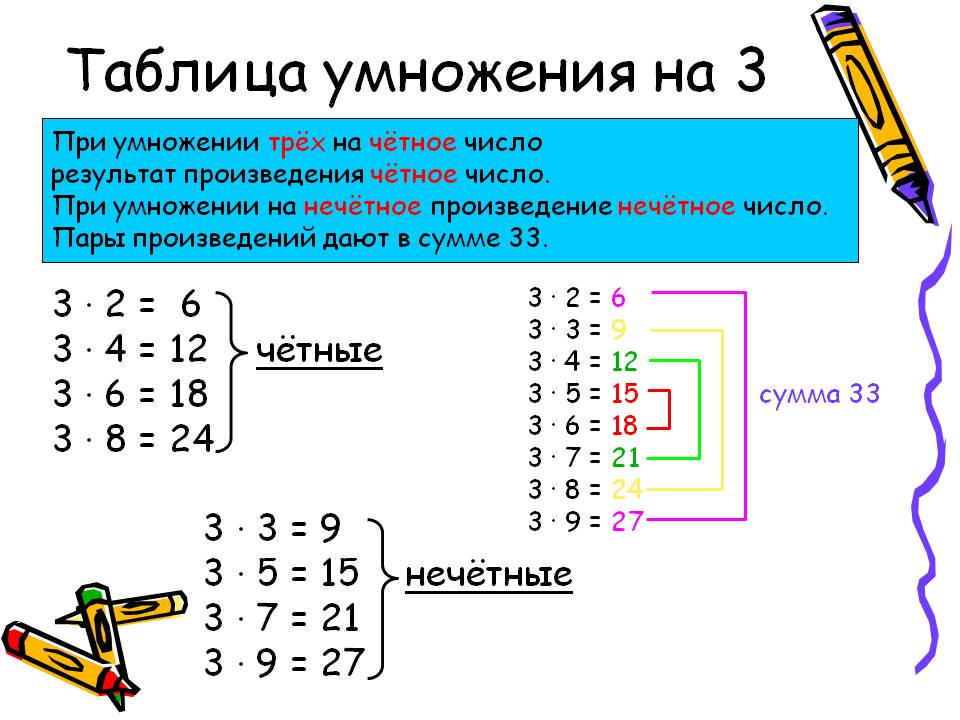 Таким образом, любой метод, который претендует на лучшее, должен быть в состоянии сделать это только в ограниченных обстоятельствах.

$\endgroup$

1

$\begingroup$

Использование исходной таблицы $n\times n$ кажется безрадостным — по сути, это проблема третьего измерения арности, но таблица Кэли дает нам только два измерения. Однако тест ассоциативности Лайта показывает, как можно систематически упростить задачу сравнения $n$ пар таблиц Кэли. Обратите внимание, что процедуру можно значительно упростить, рассматривая только операции, производные от генераторов базовой структуры.

$\endgroup$

1

$\begingroup$

Прежде всего, позвольте мне высказать личное мнение по этому поводу. Тест ассоциативности Лайта (как отмечали другие) дает характеристику, но (по крайней мере, с моей точки зрения) он не очень полезен. Действительно, мне нравится рассматривать эту трудность проверки ассоциативности таблицы как основную причину, по которой лучше вводить ассоциативные операции (в отдельных группах) через презентации. Затем вы тривиально получаете ассоциативность, поскольку ваш «объект» по определению является частным из свободного.

Теперь позвольте мне отметить, что в частном случае, когда операция является коммутативной (как в примере, который вы написали), известен альтернативный метод, который можно выполнить с помощью карандаша. Этот (на мой взгляд, совершенно неизвестный) метод принадлежит

С. КАМАЛ АБДАЛИ и был представлен в его статье « Проверка ассоциативности бинарной операции » http://www.jstor.org/stable/3613856

Я никогда не видел объяснения этого метода в книге, поэтому стоит взглянуть на эту статью (на случай, если вы сможете пройти через брандмауэр издателя). 92 \log\frac1\delta\right)$ для таблицы $n \times n$ и вероятности ошибки $\delta$. См. Rajagopalan and Schulman, FOCS 1996, SICOMP 2000. http://dx.doi.org/10.1137/S0097539797325387

Бесплатно скачать здесь.

$\endgroup$

2

$\begingroup$

Если я правильно помню, это объясняется в книге У. Кейта Николсона

Введение в абстрактную алгебру . У меня нет копии в моем офисе, но я перепроверю, когда вернусь домой.

Редактировать: Я считаю, что то, что описывается в книге, процитированной выше, и есть Тест ассоциативности Лайта, который упоминается в других ответах.

$\endgroup$

$\begingroup$

В статье Р. П. Бёрна «Таблицы Кэли и ассоциативность» (платный доступ, но доступ к JSTOR гораздо проще, чем к большинству других) предоставлено несколько интересных способов «считывания» более слабых форм ассоциативности (таких как $a(ax)=(aa )x$) из таблиц Кэли.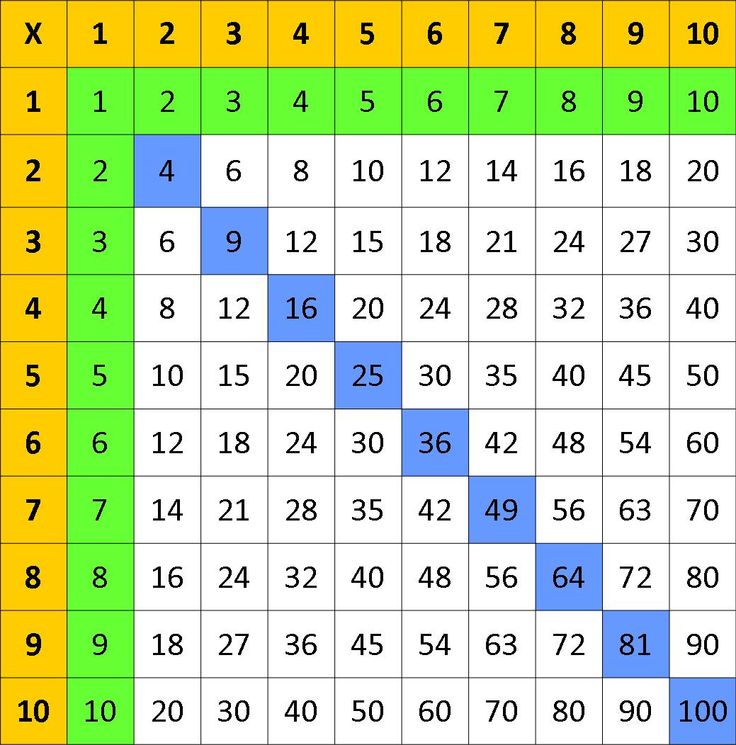

Предположительно, попытка объединить их все для получения полной ассоциативности была бы столь же плохой, как и любой другой алгоритм, но при определенных обстоятельствах этого может быть достаточно. Во всяком случае, это что-то

из исходной таблицы Кэли , а не производные.

$\endgroup$

$\begingroup$

Набор с операцией, используемой для построения четырехмерной таблицы умножения с элементами $X_{abcd} = (A(BC))D$, ассоциативен тогда и только тогда, когда $X_{abc1} = X_{1abc}$, где 1 равно единство. Так что это будет некая трехмерная симметрия четырехмерного стола.

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

абстрактная алгебра — Проверка того, принадлежит ли таблица умножения группе

Один из простых способов проверить ассоциативность — посмотреть, можем ли мы рассматривать $\{a,b,c,d\}$ как функций на некотором множестве, и рассматривать наше «умножение» как функциональную композицию, о которой вы уже должны

знать, что ассоциативна. У нас уже есть под рукой набор, сам $\{a,b,c,d\}$ (может показаться странным использовать одни и те же буквы для функций и их аргументов, поэтому я буду называть функции через $a’,b ‘, с’, d’$).

Рассмотрим пример (c): Предположим, что $a’$ является тождественной функцией:

$a'(a) = a, a'(b) = b, a'(c) = c, d'( г) = д$.

Должно быть ясно, что независимо от того, какие функции мы определяем как $b’,c’$ и $d’$, первая строка и столбец (за исключением использования штрихованных букв для записей) будут выглядеть так, как в нашем примере (c ) стол.

Теперь предположим, что $b’$ является функцией:

$b'(a) = b,b'(b) = c,b'(c) = d, b'(d) = a$ .

Пока единственная «новая» запись, которую мы можем сделать, это $b’ \circ b’$, которая по правилам композиции должна быть:

$(b’\circ b’)(a) = b'(b'(a)) = b'(b) = c\\ (b’\circ b’)(b) = b'(b'(b)) = b'(c) = d\\ (b’\circ b’)(c) = b'(b'(c)) = b'(d) = a\\ (b’\circ b’)(d) = b'(b'(d)) = b'(a) = b.$

Поскольку в нашей (c) таблице $b\circ b = c $, мы надеемся, что мы имитируем эту таблицу, определив $c’$ следующим образом:

$c'(a) = c, c'(b) = d, c'(c) = a, c'(d ) = б$.

Наконец, возьмем $d’ = b’\circ c’ = b’\circ b’\circ b’$ (без скобок, поскольку функциональная композиция ассоциативна). То есть:

$d'(a) = b'(b'(b'(a))) = b'(b'(b)) = b'(c) = d\\ d'(b) = b'(b'(b'(b))) = b'(b'(c)) = b'(d) = a\\ d'(c) = b'(b'(b'(c))) = b'(b'(d)) = b'(a) = b\\ d'(d) = b'(b'(b'(d))) = b'(b'(a)) = b'(b) = c.$

Теперь нам нужно проверить все возможные произведения по сравнивая затем с нашей таблицей в примере (с).